НЕСТАНДАРТНІ УРОКИ МАТЕМАТИКИ 8 КЛАС
 Відділ освіти
Відділ освіти
Здолбунівської районної державної адміністрації
Районний методичний кабінет
Новосілківська загальноосвітня школа І-ІІ ступенів
Здолбунівської районної ради Рівненської області
Валентина Пешко
НЕСТАНДАРТНІ УРОКИ
МАТЕМАТИКИ
8 КЛАС
2014 рік
Упорядник: В. С. Пешко
Учитель математики і фізики
Новосілківської загальноосвітньої школи І-ІІ ступенів
Здолбунівської районної ради Рівненської області
Математика . Навчальний посібник. 8 клас.
У збірнику подано різні за формою проведення нестандартні уроки з математики у 8 класі. Зміст уроків та методи і прийоми їх проведення дібрано так, щоб зацікавити учнів; розвивати їх нахили та здібності, активізувати їх мислення, пізнавальну діяльність.
Для вчителів математики.
Затверджено методичною радою Новосілківської загальноосвітньої школи І-ІІ ступенів Здолбунівської районної ради Рівненської області від 09. 02. 2018.
ПЕРЕДМОВА
Предмет математики настільки серйозний, що корисно не нехтувати
нагодами робити його трохи цікавішим
Б. Паскаль
Сучасна педагогіка і психологія математики спрямовує свої зусилля на те, щоб виявити здібності та можливості учня, максимально їх використовувати для розвитку його особистості. Цього можна досягнути не лише вдосконаленням змісту шкільного курсу математики, а й впровадженням таких методів, засобів та організаційних форм навчання, які б активізували пізнавальну діяльність учнів, розвивали їх мислення, здібності, привчали працювати самостійно і творчо.
«Зацікавити розум дитини – ось що є одним із основних положень нашої доктрини, і ми нічим не нехтуємо, щоб прищепити учневі смак, ми б сказали, навіть пристрасть до навчання», - вважав видатний математик М. Остроградський.
Прагнення вчителів досягти найкращих результатів у розв’язуванні освітніх, розвивальних і виховних завдань спонукає їх до створення нестандартних уроків, структура яких не може бути підведена під алгоритм класичного уроку, що включає організаційну частину, перевірку домашнього завдання, а також традиційних уроків, яких сьогодні виділено шість типів (урок набуття нових знань, урок застосування набутих знань, урок формування практичних умінь і навичок, урок систематизації та узагальнення, урок контролю та комбінований урок). Не вкладаються вони у рамки уроків у системі особистісно зорієнтованого й інтерактивного навчання, які теж мають чітко визначену структуру. Ці уроки одержали назву нестандартних.
Нестандартний урок – це передусім творчість, самобутність і навіть мистецтво вчителя. Такий урок може максимально стимулювати пізнавальну самостійність, творчу активність та ініціативу учнів, їх інтерес до навчання.
Розрізняють такі види нестандартних уроків: інтегровані, між предметні, театралізовані, ігрові, з різновіковим складом учнів та ін. Загалом, за формою організації нестандартні уроки бувають такі: урок-лекція, урок-практикум, урок-залік, урок-КВК, урок-подорож, урок-естафета, урок-гра, урок-аукціон.
Технологія та конкретні розробки нестандартних уроків буде розглянуто нижче.
УРОК-ЛЕКЦІЯ
Врахування психологічних та вікових особливостей учнів, недосконалість шкільних підручників, зменшення часу на вивчення математики зумовлюють необхідність проведення у середніх і особливо у старших класах уроків-лекцій. Вони можуть поєднуватися з іншими уроками. Однак, як свідчить практика, найдоцільніше використовувати вступні та підсумкові (оглядові) лекції. Учитель чітко і стисло з опорою на знання учнів, викладає матеріал, виконує записи на дошці, а учні слухають, слідкують за логікою міркувань учителя, висловлюють свої думки і конспектують матеріал у зошитах.
Вступні лекції доцільно провести на початку вивчення курсів планіметрії та стереометрії. Учитель має можливість широко розкрити мету і завдання курсу, його практичне значення, історію питань, що зацікавить учнів і активізує їх навчально-пізнавальну діяльність.
На вступних лекціях учитель розкриває загальні підходи, основні ідеї, навколо яких групується матеріал. Тим самим, ще на початку вивчення теми створюють об’єктивні можливості для переходу від абстрактного, загального до конкретного, формується теоретичне мислення учнів. Зменшується обсяг інформації необхідний для запам’ятовування, засвоєння матеріалу стає більш цілеспрямованим і міцним.
Інакше може бути побудована лекція в кінці вивчення теми. Її основна мета – систематизувати та узагальнити набуті знання й уміння учнів. Головне завдання учителя-лектора у цьому випадку – повторити вивчений матеріал, показати зв'язок між окремими фактами, згрупувавши їх навколо основних ідей та понять.
Домашнім завданням після уроку-лекції може бути складання конспекта-таблиці чи таблиці опорних сигналів, що відображають зміст теоретичного матеріалу.
Тема. ЧОТИРИКУТНИКИ.
Мета. Узагальнити і систематизувати знання учнів про чотирикутники. Розвивати творче мислення, вчити цінувати думку та працю інших. Розвивати інтерес до математики, вчити етиці та культури спілкування.
Обладнання. Таблиці «Чотирикутники».
Хід уроку.
Лекція.
План лекції.
- Означення чотирикутника. Опуклі і не опуклі чотирикутники.
- Елементи чотирикутника.
- Сума кутів чотирикутника.
- Види чотирикутників.
- Властивості чотирикутників.
- Ознаки чотирикутників.
- Взаємне розміщення чотирикутника і кола.
Матеріал лекції відомий учням. Тому для пожвавлення роботи на уроці до запитань пропонується серія задач-малюнків (таблиць). Ними можна скористатися для ілюстрації того чи іншого положення. Можна поставити перед учнями проблему – встановити, яке означення або математичний факт закодовано на певному малюнку.


УРОК-СЕМІНАР
Най частіше використовують семінари, на яких узагальнюють та систематизують знання, уміння і навички з великої теми чи кількох тем. План підготовки до семінару вчитель повідомляє на початку вивчення теми.
У планах підготовки більшості семінарів доцільно передбачати такі завдання: знати (означення, теореми, алгоритми); вміти (доводити теореми, розв’язувати конкретні задачі); підготувати реферати; виготовити таблиці, моделі; підібрати і розв’язати задачі практичного характеру тощо. Перші два завдання є обов’язковими для всіх учнів. З решти завдань одне вибирається за бажанням самого учня або за рекомендацією вчителя. При цьому враховуються інтереси та здібності кожного учня.
Семінарське заняття з математики має передбачати обов’язкову самоосвітню діяльність кожного учня і колективне обговорення й оцінку її результатів. При підготовці до семінарів можна створити групи по 3-4 учні, які працюватимуть над одним питанням. Вони самостійно визначають доповідача та співдоповідача з даного питання. На семінарських заняттях учні виступають з короткими повідомленнями, які є результатом індивідуальної та групової роботи.
Досвід проведення семінарів дозволяє виділити характерні форми діяльності учнів на самому заняті. Часто семінари розпочинаються з розминки – учні розв’язують усні вправи, що вимагають глибокого розуміння теорії. Цю частину занять можна організувати в ігровій, загальній формі. Реферати на історичні теми учні пишуть невеликі, а на занятті виступають з усними короткими повідомленнями. У кінці уроку-семінару вчитель разом з учнями визначає найцікавіше повідомлення.
На кожному занятті 1-2 учні повинні виступити з серйозними математичними повідомленнями, які носять теоретичний чи світоглядний характер. Такі повідомлення доречно прослухати самому вчителю перед самим семінаром. Якщо учні виготовляли на семінар моделі, прилади, то вони захищають свою роботу, тобто розкривають технологію виготовлення моделі, її особливості та застосування.
На семінарі потрібно вислухати відповіді з основних питань і завдань. При цьому продумати такі форми роботи, щоб учні не були пасивними слухачами, а брали активну участь у роботі. Слід заохочувати таку діяльність учнів як постановка запитань до доповідача, висловлення зауважень, доповнення, пропозиції інших способів розв’язування задачі, уточнення після відповіді, оцінювання результатів роботи тощо.
Тема. ПЛОЩІ МНОГОКУТНИКІВ
Мета. Ознайомити учнів з формулами обчислення площ трикутника, паралелограма, розглянути часткові випадки. Розвивати логічне мислення культуру мовлення, уважність, терпіння.
Обладнання. Таблиця.
Хід уроку.
І. Розминка.
Розв’язування задач за малюнками.
1). S=12см2 2). S-? 3). S-?
![]()

 а - ?
а - ?


а 20 4
ІІ. Повідомлення.
- Обчислення площі трикутника за двома сторонами і кутом між ними. Обчислення площі рівнобедреного і правильного трикутника.
- Герон Олександрійський. Формула Герона.
- Обчислення площ трикутника за сторонами і радіусом вписаного (або описаного) кола. Площа описаного многокутника.
- Обчислення площі паралелограма за його діагоналями. Часткові випадки.
- Площі подібних фігур.
ІІІ. Звіт групи учнів, які працювали над завданням.
1.Виготовлення таблиць.
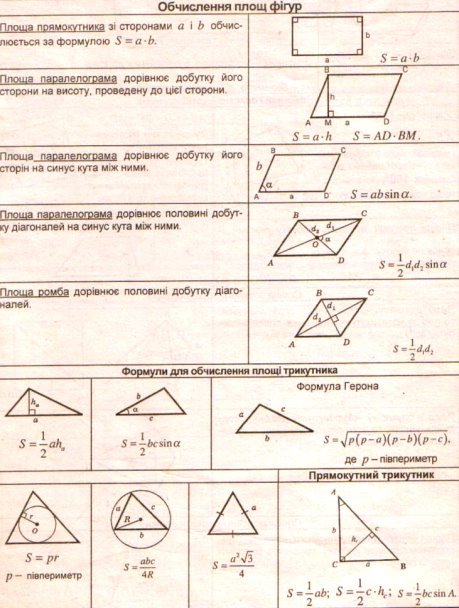
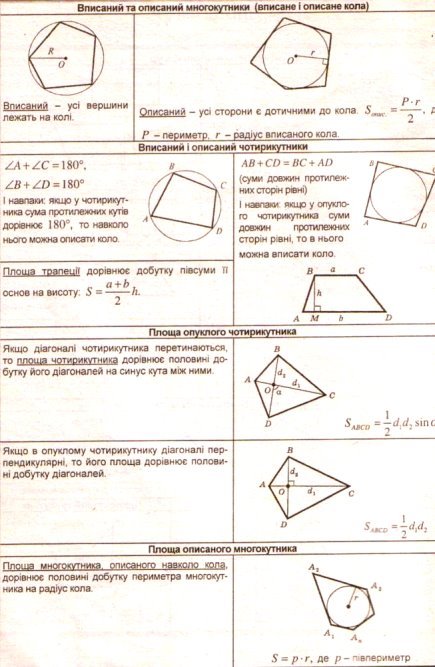
2. Задачі практичного змісту.
- Сад має форму прямокутника зі сторонами 480 м і 275 м. Скільки яблунь у ньому росте, якщо на одне дерево припадає 16 кв. м.?
- Картопляне поле прямокутної форми має розміри 450 х 260 м. Скільки тон картоплі зберуть з цього поля, якщо на одному квадратному росте 4 кущі картоплі й кожен кущ дає 2,2 кг врожаю?
- Скільки треба витратити фарби і оліфи, щоб пофарбувати підлогу в будинку прямокутної форми, розміри якого 12 м х 8,5 м, якщо на один квадратний метр підлоги витрачають 240 г фарби і 160 г оліфи?
- Скільки листів метало-черепиці потрібно, щоб вкрити гараж, дах якого має форму прямокутника з розмірами сторін 24 м х 6,5 м ? Розміри листа метало-черепиці – 1.44 м х 72 см.
- Підлога танцювального майданчика має форму ромба, діагоналі якого 8,4 м і 6,5 м . Скільки потрібно дошок розмірами 6 м х 28 см, щоб настелити підлогу ?
- Земельна ділянка має форму прямокутного трикутника, один катет якого дорівнює 40 м, а другий в 1,75 рази більший. Визначити його площу.
- Ділянка посіву цукрового буряка має форму паралелограма основа якого 1,2 км, а висота 0,8 км. За скільки днів прополе його ланка, якщо щоденно вона прополюватиме по 9,6 га ?
- Самохід косарка «КС-10» має ширину захвату 10 м. Скільки гектарів косарка викосить за 10 год роботи, якщо вона рухається зі швидкістю 4,5 км/год ?
- Тракторна сівалка «Ж-6а» має ширину захвату 6 м і за 8 год викошує 21,6 га. Скільки гектарів вона викошує за 1 год і скільки кілометрів пройде за 8 год ?
- Комбайн за 1 год скошує 2,5 га. Яку відстань він пройде за 8 год ?
- На малюнку зображений план поля. Визначити його площу.
Розміри дані в метрах.

- Підсумок уроку.
Визначення найцікавіших повідомлень і задач.
- Домашнє завдання.
Скласти і розв’язати задачу практичного змісту.
УРОК-ПРАКТИКУМ
Так називають уроки розв’язування задач із однієї чи кількох пов’язаних тем. Основний час на практикумах відводиться на кероване самостійне розв’язування задач. Керівництво роботою може здійснюватись як учителем, так і за допомогою дидактичних матеріалів.
Готуючись до уроків-практикумів учителю треба зробити значну підготовчу роботу. Слід підготовити задачі середнього, достатнього та високого (творчого) рівнів складності, продумати форми їх представлення учням. Підібраний учителем дидактичний матеріал може містити: зразки розв’язування задач; вказівки; задачі з частиною розв’язування; розв’язування з пропусками; плани розв’язування; підказки-малюнки; допоміжні запитання; теоретичні довідки; ідеї та методи розв’язування; задачі з вибіркою відповіді тощо.
Методика проведення уроків-практикумів може бути такою. Учням із достатнім та високим рівнем навчальних досягнень пропонуємо відповідні задачі для самостійного розв’язування . У цей час під керівництвом учителя учні з низьким та середнім рівнем навчальних досягнень аналізують запропоновані задачі, записують розв’язування окремих із них. Далі ці учні переходять до самостійного розв’язування аналогічних задач, а учні разом з учителем аналізують розв’язування задач достатнього рівня, а потім розв’язують творчі завдання.
Біля дошки можуть працювати учні, розв’язуючи задачі різних рівнів складності мовчки. Розв’язування цих задач слід проаналізувати із класом у кінці року. Учні, які правильно розв’язували більшість задач, бажано поставити оцінки.
Тема. ПАРАЛЕЛОГРАМ ТА ЙОГО ВЛАСТИВОСТІ.
Мета. Систематизувати і узагальнити знання учнів по темі «Паралелограм та його властивості». Розвивати практичні уміння і навички при розв’язуванні задач. Виховувати культуру математичного мовлення, самостійність у навчальній праці.
Обладнання. Таблиці із задачами.
Хід уроку.
І. Перевірка домашнього завдання.
Гра «Вибери правильне твердження».
(Учні сигналізують, що твердження правильне сигнальними картками).
1. Чотирикутник, у якого 2 сторони паралельні, паралелограм (неправильне).
2. Чотирикутник, у якого 2 сторони рівні, паралелограм (неправильне).
3. Чотирикутник, у якого протилежні сторони паралельні , паралелограм (правильне).
4. Периметр паралелограма 30 см, а сума 2 сусідніх сторін 16 см(неправильне). А якою має бути сума 2 сусідніх сторін?
5. Чотирикутник, у якого діагоналі точкою перетину діляться пополам, паралелограм (правильне).
ІІ. Розв’язування задач.
- Усні задачі.
1. Чи може один із кутів паралелограма дорівнювати 40°, а другий 50°?
2. Відомо, що в паралелограмі один кут в 2 рази більший від другого. Чи є ці кути протилежними? Чому дорівнює сума цих кутів?
3. Сума двох кутів паралелограма 100°. Чи є ці кути прилеглими до однієї сторони паралелограма? Знайти кути паралелограма.
4. Сторони паралелограма дорівнюють 3 см і 5 см. Знайти його периметр.
5. Периметр паралелограма дорівнює 20 см. знайти його сторони, якщо:
а) одна з них на 2 см більша від другої;
б) вони відносяться як 3 : 7.
2. Задачі за готовим малюнком.
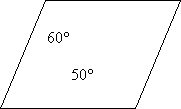
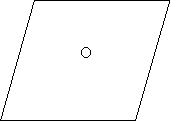
1. Які з чотирикутників, зображені на рисунку є паралелограмами?

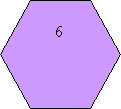
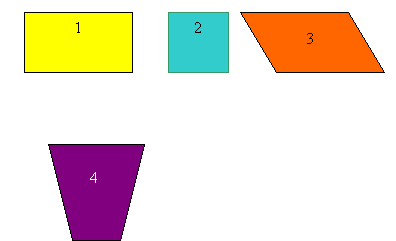
- Знайти кути паралелограма.
 B C
B C
![]() С
С
![]()
![]()
А D

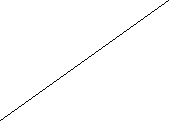 B C
B C
A D
![]() BOC =90°
BOC =90°
![]() OAD:
OAD: ![]() ODC=1:2
ODC=1:2
- Довести, що АВСД – паралелограм.
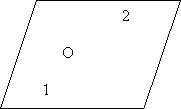

![]() B C
B C
A D
![]() AO=OC
AO=OC
3. Задачі практичного змісту.
1. Проведіть дві паралельні прямі. Відкладіть на одній із них відрізок АД, а на другій прямій – відрізок ВС, що дорівнює АД, так, щоб відрізки АВ і СД не перетиналися. Побудуйте відрізки АВ і СД.
а) Поясніть, чому чотирикутник АВСД є паралелограмом.
б) Позначте точку М так, щоб чотирикутник АВМС був паралелограмом. Чи лежать точки М, С, і Д на доній прямій?
2. Накресліть трикутник АВС і проведіть його медіану ВО. На промені ВО побудуйте відрізок ОД, що дорівнює ВО. Сполучіть точку Д з точками А і С.
а) Поясніть, чому чотирикутник АВСД є паралелограмом.
б) Позначте точку М так, щоб чотирикутник АВДМ був паралелограмом. Чи лежать точки М, С і Д на одній прямій?
4. Творчі завдання.
1. У паралелограма АВСД ВС=12 см, СД=7 см. Бісектриси кутів В і С, перетинаючи сторону АД, ділять її на три частини. Знайдіть кожну з них.
ІІІ. Підсумок уроку.
Оголошуються бали, які учні набрали в процесі розв’язування задач.
ІV. Домашнє завдання.
Знайти цікаві факти про паралелограм.
УРОК-ЛАБОРАТОРНА РОБОТА
Такі уроки є однією з форм організації самостійної навчально-пізнавальної діяльності учнів. Вони дають можливість учням більш повно і свідомо з’ясовувати математичні залежності між величинами, знайти певні закономірності, удосконалити навички вимірювань і обчислень, роботи з таблицями, графіками, діаграмами тощо.
Завдання лабораторної роботи вчитель записує на дошці або використовує графопроектор. Зміст завдань має бути зрозумілим, стислим і вичерпним. Робота може складатися з обв’язкової і додаткової частин. Під час виконання завдань учні записують у зошитах тему, мету і результати виконання роботи.
Основні етапи лабораторних робіт є:
- Актуалізація опорних знань і вмінь.
- Мотивація навчання, повідомлення теми і мети роботи.
- Інструктаж щодо послідовності виконання вимірювань, обчислень, запису результатів роботи.
- Самостійне виконання учнями (кожним, парами, по варіантах, групами) роботи. Спостереження вчителя за роботою учнів.
- Аналіз та оцінювання вчителем результатів роботи учнів.
Тема. ПОДІБНІСТЬ ПРЯМОКУТНИХ ТРИКУТНИКІВ.
Мета. Експериментально визначити висоту дерева використовуючи ознаки подібності трикутників. Розвивати практичні уміння і навички при розв’язуванні задач. Виховувати наполегливість і самостійність у навчальній праці.
Обладнання. Інструкція до лабораторної роботи.
Хід роботи.
І. Актуалізація опорних знань.
Учням пропонуються усні вправи за готовими малюнками. У ході розв’язування цих вправ учні повторюють основні поняття і властивості, вивчені в темі «Подібність трикутників».
Завдання класу.
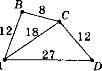
1) Чи подібні трикутники?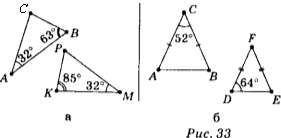
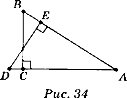
2) Дано: ∆ АВС і ∆ АДЕ – прямокутні трикутники.
Довести: ВС : ДЕ = АВ : АД
3) Учням пропонується розв’язати анаграму і виключити зайве слово.
(У кожному слові анаграми переставлені літери, потрібно відшукати правильну послідовність розміщення літер і прочитати слово)
|
КТУ |
ОСРТНОА |
РИКТТУКИН |
ЕРДАМІТ |
ЗУГАТІНЕПО |
Розв’язання:
|
КУТ |
СТОРОНА |
ТРИКУТНИК |
ДІАМЕТР |
ГІПОТЕНУЗА |
Зайве слово – «діаметр»
ІІ. Мотивація навчання.
Повідомлення теми і мети уроку.
ІІІ. Виконання роботи.
Інструктаж щодо виконання роботи. (Робота виконується в групах).
1) Візьміть мірну стрічку і, знаючи свій ріст та вимірявши тінь, яку даєте ви і дерево, що росте біля школи, знайдіть висоту дерева.
2) Проведіть необхідні вимірювання, по можливості, в сонячну погоду в різний час (в першій половині дня, опівдні, надвечір).
3) Запишіть у зошиті результати вимірювання. Виконайте необхідні обчислення.
До якого висновку ви прийшли? Запишіть його.
|
№ |
Висота учня |
Довжина тіні учня |
Довжина тіні дерева |
Висота дерева |
|
1 учень |
|
|
|
|
|
2 учень |
|
|
|
|
|
3 учень |
|
|
|
|
ІV. Підсумок уроку.
Аналіз та оцінювання вчителем результатів роботи учня.
V. Домашнє завдання.
Протяжність України із заходу на схід наближено 1 270 км, а з півночі на південь – 900 км.
1) Який треба взяти масштаб, щоб намалювати карту України найбільш можливого розміру на аркуші паперу учнівського зошита?
2) При якому масштабі карту України найбільш можливого розміру можна намалювати на аркуші паперу для креслення?
3) Намалюйте наближено кордони України, позначте точки на цій карті міста: Київ, Львів, Рівне.
УРОК-ГРА
Виникнення інтересу до математики в учнів значною мірою залежить від методики її викладання, від того, наскільки вміло буде побудована навчальна робота. Потрібно турбуватися про те, щоб на уроці кожний учень працював активно, захоплено, і використовувати це як відправну точку для виникнення та розвитку допитливості, глибокого пізнавального інтересу. Це особливо важливо робити у підлітковому віці, коли ще тільки формується, а іноді тільки зароджується постійні інтереси та нахили до певного предмета. Саме в цей період учителю треба розкрити притаманні сторони математики.
Важливу роль тут відводиться дидактичним іграм на традиційних уроках математики та урокам-іграм. Сучасна дидактика справедливо вбачає в них можливості ефективної організації взаємодії вчителя і учнів, продуктивної форми їх спілкування з елементами змагання, розкутості, інтересу.
Гра – це творчість, гра – це праця. У процесі гри у дітей формується звичка зосереджуватися, мислити самостійно, розвивається увага, уява, прагнення до знань. Захопившись, учні не замічають, що вчаться: пізнають, запам’ятовують нове, орієнтуються в незвичайних ситуаціях, фантазують. Ігри допомагають виховувати в учнів дисциплінованість, доброзичливість, почуття відповідальності та інші хороші якості.
Ідея змагання закладена в багатьох іграх, які ми із задоволенням дивимось по телебаченню. Це і «КВК», «Брейн-ринг», «Щасливий випадок», «Що? Де? Коли?» і інші. Саме форму організації цих ігор найчастіше використовують учителі при проведенні уроків-ігор з математики. Най традиційними і цікавим для учнів є також урок-казка, урок-вікторина, урок-подорож та інші.
Урок-КВК
Готуючись до уроку-КВК учні обирають двох капітанів команд, а вони почергово набирають команду. Команди придумують свою назву, девіз, готують емблему, коротке представлення і виконують домашнє завдання. Перед уроком учні кожної команди сідають за окремий ряд.
Тема. Квадратні рівняння.
Мета. Через гру формувати в учнів уміння і навички розв’язувати квадратні рівняння; розвивати логічне мислення; виховувати доброзичливість та відповідальність за результати своєї роботи.
Обладнання. Картки із завданнями, таблиця результатів конкурсів.
|
№ з/п |
Назва конкурсу |
Кількість балів І команди |
Кількість балів ІІ команди |
|
1. |
Домашнє завдання |
|
|
|
2. |
Допуск |
|
|
|
3. |
Розминка |
|
|
|
4. |
Естафета рівнянь |
|
|
|
5. |
Математична пісня |
|
|
|
6. |
Конкурс капітанів |
|
|
|
7. |
Конкурс художників |
|
|
|
|
Загальна кількість балів |
|
|
Хід уроку.
І.Організаційна частина.
Продзвенів уже дзвінок,
Всі прийшли ви на урок.
Математика тепер у нас,
Позмагається весь клас.
Сьогодні ж виявим знання
У грі чудовій – КВК.
І перемога тих чекає,
Хто знань побільше має.
ІІ. Основна частина.
- Домашнє завдання.
Виставляється кількість балів за домашнє завдання, слід урахувати:
- математична газета;
- емблема команди;
- привітання суперникам;
- гасло команди
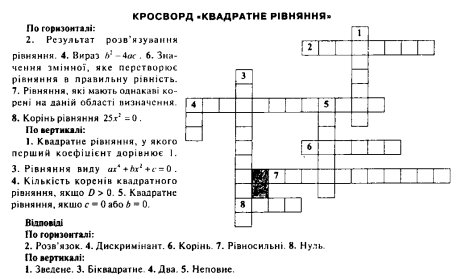
- Допуск.
Розгадати кросворд «Квадратні рівняння». Хто швидше розв’яже, той має найбільшу кількість балів.


- Розминка.
Дибав до Києва сивий дідусь.
І зустрів він 12 бабусь,
По кошику кожна несла,
В кожному кошику кішка була.
12 у кожної з них кошенят,
Ще по четверо держать в зубах мишенят.
І сивий дідусь наш замислився тут:
Скільки кошенят і скільки мишенят
До Києва наші бабусі несуть?
(Ніскільки, бо усі йшли назустріч, а до Києва йшов
він).
1 команда
1. Чи є число -1 коренем рівняння –х2+2х-2=0?
2. При якому значенні k рівняння 16х2+ kх+9=0 має лише один корінь?
3. Скласти зведення квадратне рівняння за його коренями х1=3, х2= -1
2 команда
1. Чи є число -2 коренем рівняння х2+3х+2=0?
2. При якому значенні k рівняння 25х2- kх+1=0 має лише один корінь?
3. Скласти зведення квадратне рівняння за його коренями х1=1, х2= -3.
- «Естафета рівнянь»
На дошці записано для кожної команди записано стільки рівнянь, скільки є учнів.
1 команда 2 команда
а) х2-11х+30=0; а) х2-х-90=0;
б) 3х2-5х+4=0; б) 5х2+4х+7=0;
в) х2-7х+12=0; в)х2+2х-35=0;
г) х2=4х+5; г)х2-8=4-4х;
д) (х+4)2=3х+40; д) (2х-3)2=11-19;
е) 4х2-2 = х(10х-9). е) х2-1 =11(х+1).![]()
3 2
- Математична пісня.
Представники команд по черзі співають куплети пісень, де зустрічаються числа і числівники.
- Конкурс капітанів.
До дошки одночасно виходять обидва капітани і розв’язують відповідні завдання.
1 команда
Один із коренів рівняння х2-5х+с=0 дорівнює 3. Знайдіть другий корінь і вільний член с.
2 команда
Один із коренів рівняння х2+bх-9=0 дорівнює 9. Знайдіть другий корінь і коефіцієнт b.
Члени команд розв’язують завдання своїх капітанів самостійно в зошитах. Якщо капітан не може справитися зі своїм завданням, то просить допомоги у команди. За допомогу знімається половина балів цього конкурсу.
7. Конкурс художників.
Двоє учасників від кожної команди виконують такі завдання:
- одночасно пишуть лівою рукою 9, а правою – 6;
- обома руками пишуть 8;
- не відриваючи крейду від дошки, повинні намалювати лебедя або гусака.
ІІІ. Підсумок уроку.
Цей урок міцніше нас здружив
З цікавою і дивною наукою,
Щоб вогник знань у класі жив –
Він буде запорукою.
Мов естафету, вогник знань
З рук в руки передайте,
Побільше різних запитань
Дорослим задавайте.
Гра закінчена. Учитель підводить підсумки, оголошує команду переможця, «нагороджує» найактивніших учасників КВК оцінками, дає домашнє завдання.
Урок «Свято задачі»
Тема. Розв’язування задач за допомогою квадратних рівнянь.
Мета. Удосконалення вмінь та навичок роз’язування різних типів задач на складання квадратних рівнянь. Нормування вмінь виявляти закономірності, узагальнювати, проводити міркування за аналогією. Розвиток творчого мислення, активності, пізнавальної самостійності. Виховання математичної мови, культури математичних записів на дошці і в зошитах.
Девіз уроку. «Математику не можна вивчити і спостерігати як це роблять інші». А. Нівен
Хід уроку.
І. Організаційна частина.
Хочу всіх вас привітати
Успіху вам побажати, -
Всім, хто вміє задачі розв’язувати,
Любить думати і міркувати,
Правильну відповідь умить відшукати.
ІІ. Вступне слово вчителя.
Могутні крила сучасної науки в нестримному леті підносять нас до вершин пізнання, допомагають осягнути таємниці Всесвіту. Рвуть пута земного тяжіння космічні кораблі, павутиною вкрив земну кулю мобільний зв’язок, працює приручений атом. Те, що вчора було фантастикою, стає сьогодні невід’ємною частиною нашої дійсності. Але з поміж усіх турбот науки найголовнішою залишається одна - людина, найдосконаліше творіння живої природи.
Лише велика попередня праця, напружена робота думки, розуму, інтуїція, творче натхнення ведуть до результатів. Варто згадати слова видатного англійського філософа Френсіса Бекона: «У кожній людині природа проростає або злаками, або бур’яном. Нехай же вона своєчасно поливає перше і знешкоджує друге». Тому слід розвивати свої можливості, в процесі навчання вдосконалювати свої задатки. Якщо до цього додати наполегливість, силу волі, працелюбство, то з кожного учня з часом сформулюється особистість, яка зможе досягнути висот у певному виді діяльності. працюючи активно сьогодні на уроці ви збагатите свої знання з математики.
Завдання нашого уроку – користуючись основними властивостями рівнянь, знайти загальні методи і прийоми розв’язування задач на складання квадратних рівнянь. Сьогодні у нас «Свято задачі» Розпочнемо його.
ІІІ. Актуалізація опорних знань.
Гра «Закінчіть речення».
- Рівність , яка містить невідоме число, позначене буквою, називається …
- Значення змінної, що перетворює рівняння в правильну рівність, називається …
- Квадратним рівнянням називається рівняння виду …
- Дискримінант квадратного рівняння обчислюється за формулою …
- Формула коренів квадратного рівняння має вид …
- Якщо ми розв’язуємо задачу на складання рівняння, то:
1) треба позначити за Х …
2) виразити через Х …
3) скласти …
4) пояснити …
ІV. Розв’язування задач.
 На сьогоднішнє свято до нас завітали казкові герої. У кожного із них для нас подарунок-задачка, яку ми повинні розв’язати. Якщо у нас виникнуть труднощі, то герої допоможуть
На сьогоднішнє свято до нас завітали казкові герої. У кожного із них для нас подарунок-задачка, яку ми повинні розв’язати. Якщо у нас виникнуть труднощі, то герої допоможуть
№1. (задача від Попелюшки) На середині відстані між нашим будинком і королівським замком, моя карета затрималась на 20 хв. Щоб ліквідувати запізнення на бал, кучер збільшив швидкість на 10 км/год. Потрібно відшукати початкову швидкість карети, якщо відстань між пунктами 200 км.
 №2. (задача від Чародія) Я задумав три послідовні цілі числа. Сума квадратів цих чисел дорівнює 194. Відгадайте, будь-ласка, ці числа.
№2. (задача від Чародія) Я задумав три послідовні цілі числа. Сума квадратів цих чисел дорівнює 194. Відгадайте, будь-ласка, ці числа.
Відпочинок.
Відгадай загадку.
Загадкове, нам знайоме,
В ньому є щось невідоме.
Його треба розв’язати,
Тобто корінь відшукати.
Кожен легко, без вагання
Відповість, що це …
(Рівняння)
Ми ділили, додавали,
Там де треба знак міняли,
Різні спрощення робили,
Корені знайти зуміли
Ось і зроблено завдання –
Розв’язали ми …
(Рівняння)
Їх в підручнику багато,
Кожну треба розв’язати.
Не будьте ви ледачі,
Розв’язуйте …
(Задачі)
Нам вірний та надійний друг,
Без нього дехто – як без рук.
І кнопки, і екран він має,
Нам результат доповідає.
Обчислень він організатор,
Чудовий прилад …
(Калькулятор)

№3. (задача від жителів країни Чудес) Жителі нашого містечка обмінялись своїми SMS-повідомленнями. Відгадайте скільки жителів у містечку, якщо для обміну потрібно було 600 SMS-повідомлень.
 №4. (задача від Шпунтика і Гвинтика) Ми двоє, працюючи разом, можемо виконати деяку роботу за 3 год 36 хв, а працюючи окремо, половину цієї самої роботи Шпунтик виконує на 1,5 год швидше, ніж Гвинтик. За який час може виконати цю роботу кожен із нас, працюючи окремо?
№4. (задача від Шпунтика і Гвинтика) Ми двоє, працюючи разом, можемо виконати деяку роботу за 3 год 36 хв, а працюючи окремо, половину цієї самої роботи Шпунтик виконує на 1,5 год швидше, ніж Гвинтик. За який час може виконати цю роботу кожен із нас, працюючи окремо?
V.Підсумок уроку.
Виберіть рівняння, що задовольняє умову задачі.
Знайдіть катети прямокутного трикутника, коли відомо, що один із катетів на 2см менший від другого, а гіпотенуза дорівнює 10см.
- х2+(х-2)2=(10-2)2
- х2+(2-х)2=102
- х2+(2х)2=102
- х2+(х+2)2=102
Урок з елементами гри.
Тема. Стандартний вигляд числа.
Мета. Формувати уміння перетворювати вирази із степенями з цілим показником, дати уяву про стандартний вигляд числа.
Обладнання. Плакат із кросвордом, таблиця із задачею.
Хід уроку.
І. Перевірка домашнього завдання.
- Наявність письмового завдання перевіряють чергові або консультант.
2) Інтелектуальна гра «Мозковий штурм»
Швидко відповісти на запитання
- Подайте у вигляді добутку дріб:
1,3 ; а6 ; y ;
х b7 (x+9)2
2) Подайте у вигляді степеня з від’ємним показником:
1 ; 1 ; 1 .
23 34 8а3
3) Спростити вираз:
m-7:m-5; (a-1b4)-2; y-5xy3
4) Знайти значення виразу:
(-3)-4; (1,7)2х(1,7)-2
ІІ. Повторення вивченого.
 Загадка-кросворд (плакат)
Загадка-кросворд (плакат)
|
|
2. |
|
||||||||
|
|
||||||||||
|
1. |
|
|
|
|
|
3. |
|
|
5. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
||||||||
|
|
|
|
||||||||
|
|
|
|
||||||||
|
4. |
|
|
|
|
|
|
||||
|
|
|
|
||||||||
|
|
||||||||||
|
|
||||||||||

1. Коли друзів є багато,
І усі у справі,
Тоді мене складеним
Вони називають.
Якщо друг лиш одиниця,
То простим всі кличуть.
Тож скажіть, будь ласка, любі,
Як же звуться мої друзі?
(дільники)
2. Чи базис, чи фундамент, чи основа,
Яке до степеня ви доберете слово?
(основа)
3. Більше я, ніж число,
В певну кількість раз.
Я не він, не вона,
А воно щораз!
(кратне)
4. Я показник плюс основа,
Назвіть мене одним словом.
(степінь)
5. Маленьким мене пишуть
В горі біля основи,
Та сил багато маю.
Я множу знову й знову
Основу на основу.
(показник)
ІІІ. Пояснення нового матеріалу.
Бесіда вчителя.
У науці та техніці зустрічаються великі числа (наприклад, відстань від Землі до Сонця 150 000 000 км) та дуже малі числа (діаметр молекули води 0, 0 000 000 003 м).
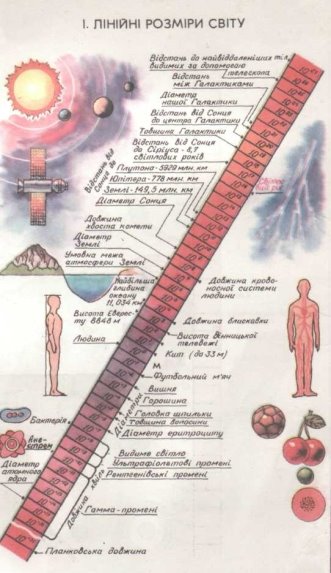
Над такими числами незручно проводити дії, їх незручно читати і записувати. У такому разі зручно користуватися стандартним записом числа: це запис ах10n ,де п – ціле число, 1 ≤ а < 10.
Число п називають порядком числа.
1 083 000 000 000 = 1,083х1012
0,000 000 003 = 3х10-9
Порядок числа дає уявлення про те, велике чи мале число.
Великий додатний порядок означає, що число дуже велике. Так, у першому випадку порядок дорівнює 12. Це число велике. Порядок (- 10) у другому випадку означає, що число дуже мале.
Приклади.
- Подати у стандартному вигляді числа:
а = 6 275 000 000;
в = 0,000 804.
ІV. Розв’язування вправ.
Взаємоконтроль при виконанні вправ
Учні працюють у парах: один – «спеціаліст», другий – «рецензент». Потім міняються ролями. У ролі арбітру – вчитель.
Завдання.
Учень А Учень Б
1. Назвіть порядок числа, яке подане в стандартному вигляді:
1,2х109 3,6х103
2,7х10-3 6,3х10-1
2. Запишіть у стандартному вигляді числа:
52 000 000 2 180 000
0,002 81 0, 000 035
3. Знайти значення виразу:
125-1х52 16-3 х 46
(62)6:614 120 х (12-1)2
3,2х-1у-5 х 5 ху 0,6с2d4 х 1с-2d-4
8 3
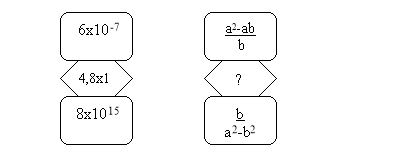
- Підсумки уроку
Учитель ще раз підкреслює важливість теми, що вивчається, для практичного застосування у фізиці, хімії, астрономії. Пропонує учням знайти невідомий вираз:
Урок-подорож.
Тема. Квадратний корінь.
(Степінь… корінь – дивись в корінь)
Мета. Через гру закріпити вміння учнів виконувати дії з квадратними коренями, розвивати в учнів інтелектуальні та творчі здібності; виховувати дисциплінованість, відповідальність, почуття прекрасного.
Обладнання. Картки із завданнями.
На дошці напис: «Саме на подоланні труднощів росте і розвивається математик».
О. Хінчин
Хід уроку.
І. Організаційна частина.
Сьогодні у нас незвичайний урок.
Сьогодні ми зробимо ще один крок
В країну зіркову, в країну чудову,
Що нас так чекає й збагачує розум.
Щоб нам швидше до неї потрапить,
Потрібно екзамен кмітливості скласти.
Тож сядьте рівненько, стежте уважно,
Щоб здогадатись вам було неважко.
ІІ. Подорож.
Сьогодні ми вирушаємо у мандрівку. А куди , ви дізнаєтесь, коли розв’яжете приклади. А потім усі відповіді розташуєте в порядку зростання.
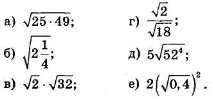
Підпишіть під числами відповідні букви і прочитайте, куди ми мандруємо.
К О С М О С
Отже, ми вирушаємо у мандрівку в космос, де побував і наш український космонавт Л. Каденюк на американському кораблі «Шаттл».
При мандрівці в космосі весь час потрібно робити обчислення, щоб визначити місце знаходження корабля, його прибуття. А в цій мандрівці перевіримо ваше вміння знаходження раціональних способів розв’язування вправ, логічно мислити, виконувати дії додавання, віднімання, множення виразів, що містять квадратні корені; скорочувати дроби.
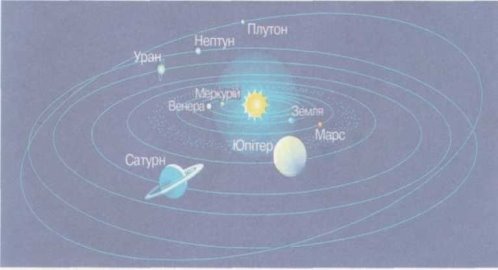
наша математична подорож буде далека і цікава і проходитиме по планетах Сонячної системи.
Модель Сонячної системи представлена на малюнку-схемі. Всі планети Сонячної системи (Меркурій, Венера, Земля, Марс, Юпітер, Сатурн, Уран, Нептун, Плутон) обертаються навколо Сонця, а також навколо своєї осі.
Наша планета Земля має єдиний природній супутник – Місяць, який обертається навколо Землі. Нам потрібно розв’язати деякі приклади щоб попасти на Місяць.

Розрахунок ми зробили правильно і успішно прибули на Місяць. В космічний порт Місяця пропускають лише тих, хто правильно вміє розв’язувати рівняння.
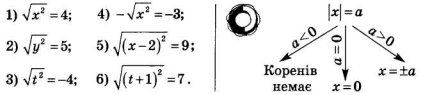
Молодці! Рівняння розв’язані добре. З Місяця ми вилітаємо на Марс, але, щоб вилетіти, потрібно порівняти величини.
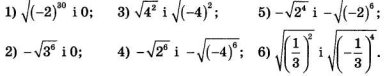
При посадці на Марс в командира корабля виникла проблема, йому потрібно розв’язати деякі завдання.

А щоб повернутися на Землю ми повинні з вами подолати ще трохи труднощів. Повинні справитись із наступними завданнями

ІІІ. Підсумок уроку
Вітаю всіх на нашій планеті Земля!
Визначте, яке число треба записати замість «?»
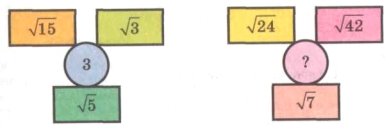
Список використаної літератури:
- М. В.Підручна, Г. М Янченко. Позакласна робота 8-9 класи.
- М. В Підручна, Г. М Янченко. Позакласна робота 5-7 класи.
- М. Дзюбинська та інші. Математика після уроків 5-11 класи.
- С. Вихор. Нестандартні уроки математики 5-6 класи.
- В.М. Козира. Технологія уроку з математики 5-11 класи.
- Л.В. Колесникова. Алгебра плани-конспекти уроків 8 клас.
- Г.М. Будняк та інші. Уроки геометрії в 8 класі.
- Л.С. Карнацевич та інші. Геометрія. Плани-конспекти уроків 9 клас.

1


про публікацію авторської розробки
Додати розробку
