Невизначений інтеграл, його властивості та методи обчислення

Дистанційне навчання

 

Дисципліна «ВИЩА МАТЕМАТИКА»

 

ЛЕКЦІЯ

 

Тема: Невизначений інтеграл, його властивості та методи обчислення.

Мета: пригадати зі ШКМ що називається первісною функції, які її властивості; ознайомитись з поняттям невизначеного інтеграла, його властивостями, геометричним змістом, таблицею основних інтегралів; дізнатись як обчислюються невизначені інтеграли безпосереднім інтегруванням, методом заміни змінної, інтегруванням частинами.

Ключові поняття і терміни:

 первісна функції;

 властивості первісної;

 операція інтегрування;

 невизначений інтеграл;

 геометричний зміст невизначеного інтеграла;

 властивості невизначеного інтеграла;

 методи інтегрування.

План лекції

1.Поняття первісної. Властивості первісної.

2.Задача інтегрування. Невизначений інтеграл.

3.Властивості невизначеного інтеграла.

4.Таблиця основних інтегралів (формули інтегрування).

5.Методи інтегрування (безпосереднє інтегрування, інтегрування заміною змінної, інтегрування за частинами).

 

Завдання для виконання

1. Ознайомитись з новим матеріалом. Розібрати приклади, зробити конспект.
2. Відповісти на контрольні питання (усно).
3. Обчислити невизначені інтеграли:

а) беспосереднім інтегруванням:

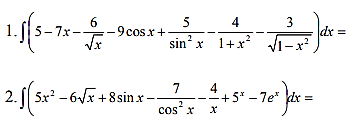
б) інтегруванням заміною змінної:

в) інтегруванням за частинами:

.

Рекомендована література

1. Павліщев В.І. Вища математика. Невизначений інтеграл (у прикладах і задачах) навч.посіб. – Д.: НГУ, 2015. – 71 с. http://ir.nmu.org.ua/bitstream/handle/123456789/146945/%D0%9D%D0%B5%D0%BE%D0%BF.%D0%B8%D0%BD.%D0%BF%D0%BE%D0%BB%D0%BD%20%D0%BA%D0%BD%D0%B8%D0%B3%D0%B0_%D0%A3%D0%9A%D0%A0_29_05_2015.pdf?sequence=1&isAllowed=y
2.     Барковський В.В. Барковська Н.В. Математика для економістів: Вища математика. -К.: НАУ, 2005.-397с.
3.     Вища математика в прикладах і задачах: Навчальний посібник/ Л.І. Турчанінова, О.В. Доля. –  Київ: Ліра - К- 2018. – 348 с.
4.     Пасічник Я.А. Математика для економістів: Підручник.-Острог: видавництво Національного університету «Острізька академія», 2010.-432с.

 

МАТЕРІАЛ ЛЕКЦІЇ

1. Поняття первісної. Властивості первісної.

 

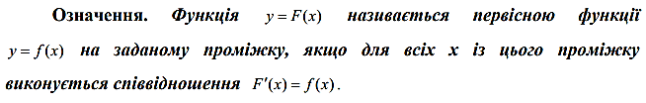
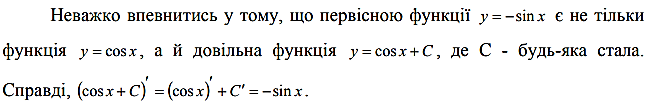
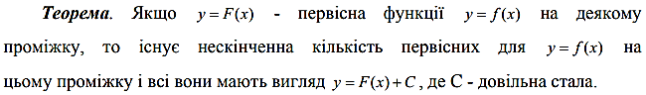
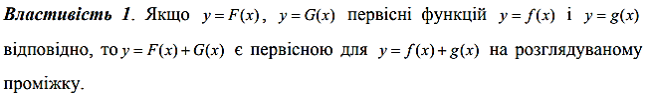
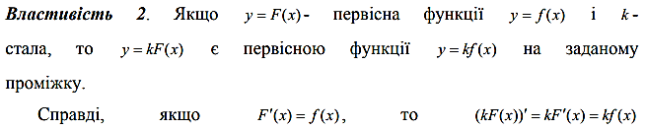
2. Задача інтегрування. Невизначений інтеграл.

Означення. Операція знаходження первісних для функції f(x) називається інтегруванням f(x).

Задача інтегрування функції на проміжку полягає у тому, щоб знайти всі первісні функції на цьому проміжку, або довести, що функція не має первісних на цьому проміжку.

Для розв’язування задачі інтегрування функції достатньо знайти одну будь-яку первісну на розглядуваному проміжку, наприклад F(x), тоді (за теоремою про множину первісних) F(x) + С — загальний вигляд всієї множини первісних на цьому проміжку.

Означення. Функція F(x) + С, що являє собою загальний вигляд всієї множини первісних для функції f(x) на проміжку І, називається невизначеним інтегралом від функції f(x) на проміжку І і позначається

 , ,  (1)

де — знак невизначеного інтеграла;

f(x) — підінтегральна функція;

f(x)dx — підінтегральний вираз;

dx — диференціал змінної інтегрування.

Геометричний зміст невизначеного інтеграла полягає в тому, що функція є рівняння однопараметричної сім’ї кривих, які утворюються одна з одної паралельним перенесенням уздовж осі ординат (рис. 1).

Теорема  (Коші). Для існування невизначеного інтеграла для функції f(x) на певному проміжку достатньо, щоб f(x) була неперервною на цьому проміжку.

Зауваження. Виявляється, є такі невизначені інтеграли від елементарних функцій, які через елементарні функції не виражаються, наприклад:

, , ,

існують у кожному із проміжків області визначення, але записати їх через основні елементарні функції не можна; в такому розумінні ці інтеграли називають «неінтегровними».

3. Властивості невизначеного інтеграла.

а) Властивості, що випливають із означення (1).

І. Похідна від невизначеного інтеграла дорівнює підінтегральній функції .

ІІ. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу.

ІІІ. .

б) Властивості, що відображають основні правила інтегрування.

IV. Сталий множник, що не дорівнює нулю, можна виносити з-під знака інтеграла, тобто

 

V. Невизначений інтеграл від суми функцій дорівнює сумі невизначених інтегралів від цих функцій, якщо вони існують, тобто

 

4. Таблиця основних інтегралів (формули інтегрування).

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;  

8. ;

9. ; 

10. ;

11. ; 

12. ;

13. ; 

14. ;

15.          ;

16.          ;
17.          ;
18.          ;
19.          ;
20.          ;
21.          .

 

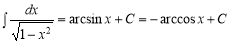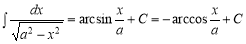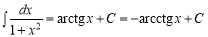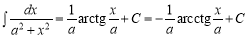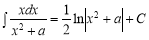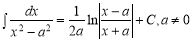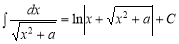В економіці часто застосовують такі функції, як y=lnx та y=1-e^-x. Інтеграли від цих функцій:

    ;

   

 

5. Методи інтегрування (безпосереднє інтегрування, інтегрування заміною змінної, інтегрування за частинами)

Таблицю невизначених інтегралів необхідно доповнити способами або методами інтегрування. Одним з основних методів є безпосереднє інтегрування: після перетворення підінтегрального виразу виявляються табличні інтеграли.

Другий ефективний спосіб інтегрування – заміна змінної або підстановка. Третім основним методом є інтегрування за частинами. Суть кожного методу – звести інтеграл до табличного вигляду.

Приклади безпосереднього інтегрування (за таблицею та основними правилами інтегрування):

. Справді, .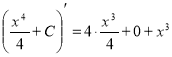

 

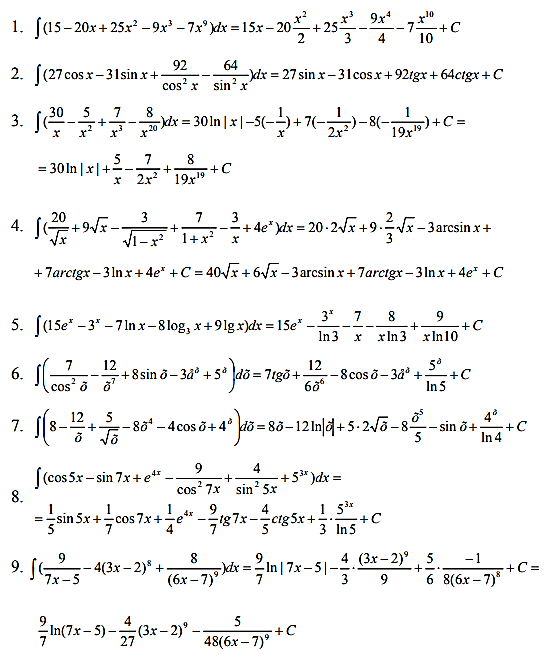
Із означення невизначеного інтеграла випливають такі властивості інтегрування:

(метод заміни змінних, метод підстановки);

             (інтегрування частинами).

Приклади (метод заміни змінних, метод підстановки)

1.   Знайти 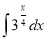. Виконуємо заміну (підстановку) x/4=t.

      Тоді dx=4dt, отже,

             

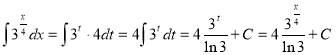
2. Знайти  .    Виконуємо заміну 2x=t, звідки  2dx=dt. Тепер

           

3. Знайти . При заміні x=t³-1 маємо x+1=t³ , dx=3t²dt   і далі

           

                         

4. Знайти    (заміна  4x=t).

5. Знайти    (заміна 6x-5=t).

Інтегрування частинами потребує певних навиків. Розглянемо цей спосіб на прикладах.

Приклади.

1. Знайти інтеграл . Позначимо вираз lnx через u, а вираз x³dx через dv. Знаходимо  du та v:

                    

Отже,

.

2.   Знайти . Позначимо u=x, dv=e^2xdx. Звідси  du=dx, v=(1/2)e^2x. Тоді

           .

ЗАУВАЖЕННЯ:

8. З якими методами інтегрування ви познайомились? У чому полягає суть кожного методу?