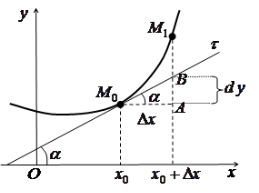Диференціал функції. Застосування диференціального числення до дослідження функцій та побудови графіків.
Дистанційне навчання
Дисципліна «ВИЩА МАТЕМАТИКА»
ЛЕКЦІЯ
Тема: Диференціал функції. Застосування диференціального числення до дослідження функцій та побудови графіків.
Мета: Ознайомитись з поняттям диференціала функції та його застосуванням для наближених обчислень; дізнатися як диференціальне числення застосовують до дослідження функцій та побудови графіків.
План
1. Диференціал функції та його застосування до наближених обчислень.
2. Застосування диференціального числення до дослідження функцій та побудови графіків.
2.1. Область визначення, парність, періодичність, монотонність функції.
2.2. Ознаки зростання та спадання функції.
2.3. Точки екстремуму і екстремуми функції.
2.4. Найбільше та найменше значення функції на проміжку.
2.5. Опуклість вгору і вниз функції. Точки перегину. Асимптоти графіка функції.
2.6. Загальна схема дослідження функції та побудова її графіка.
Рекомендовані інформаційні джерела
- https://www.youtube.com/watch?v=YGPggnLqzAU Диференціал функції та його застосування для наближених обчислень.
- http://matan.kpi.ua/public/files/Konspekt%20Dyferencialne%20ta%20integralne%20chyslenia.pdf Диференціальне та інтегральне числення функцій однієї змінної. Конспект лекцій. (І курс І семестр) / В.О.Гайдей, Л.Б.Федорова, І.В.Алєксєєва, О.О.Диховичний. — К: НТУУ «КПІ», 2013. — 104 с.
Диференціальне числення – розділ математики, в якому розглядається дослідження функцій за допомогою похідних та диференціалів.
1. ДИФЕРЕНЦІАЛ ФУНКЦІЇ ТА ЙОГО ЗАСТОСУВАННЯ.
 (*)
(*)
Геометричний зміст диференціала
Нехай ![]() ,
, ![]() та існує
та існує ![]() . За означенням диференціала
. За означенням диференціала ![]() .
.
|
|
Скористаємося геометричним змістом похідної:
З трикутника
Отже, диференціал функції |
Застосування диференціала в наближених обчисленнях:
Формула (*) дозволяє знаходити значення функції ![]() в точці
в точці ![]() , якщо відомі значення
, якщо відомі значення ![]() і
і ![]() , з точністю
, з точністю ![]() .
.

![]()
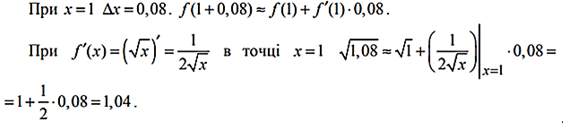
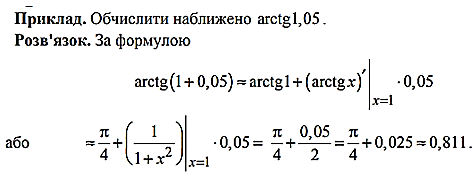
Більш детально матеріал «Диференціал функції та його застосування до наближених обчислень» поданий у відео: https://www.youtube.com/watch?v=YGPggnLqzAU
Правила знаходження диференціалів
З правил знаходження похідної випливають правила знаходження диференціала.
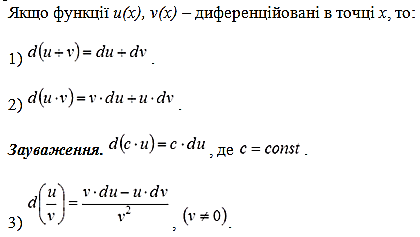
ІІ. ЗАСТОСУВАННЯ ДИФЕРЕНЦІАЛЬНОГО ЧИСЛЕННЯ ДО ДОСЛІДЖЕННЯ ФУНКЦІЙ ТА ПОБУДОВИ ГРАФІКІВ
Дослідити функцію, задану аналітичним виразом y=f(x), означає визначити такі її характеристики: область визначення; парність чи непарність; періодичність; монотонність; екстремуми; найбільше і найменше значення в заданому відрізку. Якщо є точки розриву функції, то необхідно дослідити її поведінку поблизу цих точок.
Для графічного зображення функції необхідно додатково визначити: точки перетину графіка з осями координат; опуклість його; точки перегину; асимптоти.
2.1. Область визначення функції, парність, періодичність, монотонність функції.
Означення. Якщо кожному значенню x з деякої числової множини X за певним правилом поставлене у відповідність єдине число y , то кажуть, що y є функція від x і записують y = f (x) .
Означення. Сукупність значень x, при яких функція y існує, називається областю визначення функції.
Означення. Нехай функція y = f (x) визначена в області, симетричній відносно початку координат. Тоді, якщо f (x ) = - f (x) , то функція називається непарною, а при f (x ) = f (-x) – парною.
Означення. Функція називається періодичною, якщо існує таке дійсне число l≠0 , що, при будь-яких значеннях аргументу x із області визначення
f (x) = f (x + kl) ,
де k – ціле число, l – період.
Означення. Якщо для двох будь-яких різних значень аргументу x1 і x2 з області визначення із нерівності x1 < x2 виконуються нерівності:
f (x1 ) < f (x2 ) , то функція називається зростаючою,
f (x1 ) ≤ f (x2 ) , то – не спадною,
f (x1 )> f (x2 ), то – спадною,
f (x1 )≥ f (x2 ), то – не зростаючою.
Зростаючі, спадні, не зростаючі, не спадні функції називаються монотонними.
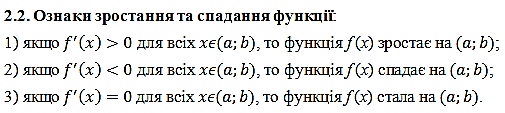
- Точки екстремуму і екстремуми функції
Точку x0 називають точкою локального максимуму ( або мінімуму) функції f(x), якщо існує такий окіл ![]() точки x0, який належить області визначення функції, і для всіх x0 з цього околу виконується нерівність
точки x0, який належить області визначення функції, і для всіх x0 з цього околу виконується нерівність
![]()
![]()
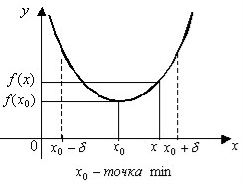
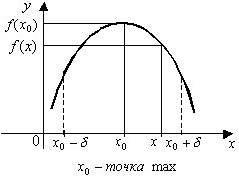
Геометричний зміст означення зрозумілий з рисунків.

Точки, в яких похідна дорівнює нулю, називають стаціонарними.
Точки, в яких похідна дорівнює нулю або не існує, називають критичними. Критичні точки – це точки можливого екстремуму.

Іншими словами, якщо при переході зліва направо через критичну точку x0 знак похідної ![]() змінюється з плюса на мінус, то x0 – точка локального максимуму; якщо знак похідної змінюється з мінуса на плюс, то x0 – точка локального мінімуму; якщо похідна не змінює знак, то в точці x0 екстремум відсутній.
змінюється з плюса на мінус, то x0 – точка локального максимуму; якщо знак похідної змінюється з мінуса на плюс, то x0 – точка локального мінімуму; якщо похідна не змінює знак, то в точці x0 екстремум відсутній.
Приклад 1
Знайти інтервали зростання та спадання функції
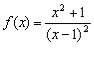
Розв’язання
Область визначення ![]() . Знайдемо похідну
. Знайдемо похідну
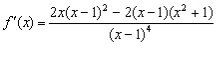
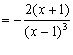 .
.
Похідна ![]() дорівнює нулю при х=-1 і не існує при х=1.
дорівнює нулю при х=-1 і не існує при х=1.
Відмічаємо ці точки на числовій прямій ( при цьому пам’ятаємо про область визначення функції) і визначаємо знак похідної на кожному з інтервалів: 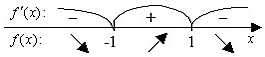
Таким чином, функція спадає , якщо ![]() , і зростає на інтервалі
, і зростає на інтервалі ![]() .
.
- Найбільше та найменше значення функції на проміжку
Не слід плутати локальний максимум (мінімум) з найбільшим (найменшим) значенням функції, якого вона досягає на відрізку. Локальних максимумів і мінімумів функція може мати декілька, тоді як найбільше значення (його ще називають абсолютним максимумом), якщо воно існує, єдине. Це саме стосується і найменшого значення (абсолютного мінімуму) функції.
Щоб знайти найбільше і найменше значення функції ![]() на проміжку
на проміжку ![]() , потрібно:
, потрібно:
1) знайти похідну ![]() і визначити критичні точки даної функції;
і визначити критичні точки даної функції;
2) обчислити значення функції в тих критичних точках, що належать інтервалу (a;b), а також в точках a і b;
3) серед одержаних значень вибрати найбільше і найменше.
Приклад 2.
Знайти найбільше та найменше значення функції ![]() на відрізку
на відрізку ![]() .
.
Розв’язання.
Знайдемо похідну
![]() .
.
Оскільки функція визначена при ![]() , то критичну точку знаходимо з умови
, то критичну точку знаходимо з умови ![]() , тобто
, тобто
![]() .
.
Ця точка не належить проміжку ![]() . Тому обчислюємо лише значення функції на кінцях відрізка.
. Тому обчислюємо лише значення функції на кінцях відрізка.
Маємо ![]() ,
, ![]() .
.
Таким чином,
![]() ,
, ![]() .
.
- Опуклість вгору і вниз функції. Точки перегину. Асимптоти графіка функції.
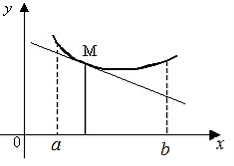
Крива ![]() називається опуклою на інтервалі (a;b), якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі.
називається опуклою на інтервалі (a;b), якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі.
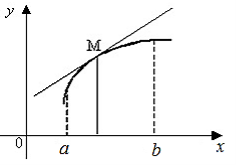
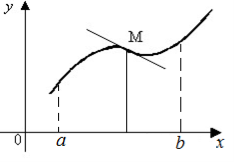
Крива ![]() називається вгнутою на інтервалі (a;b), якщо всі її точки, крім точки дотику, лежать вище довільної її дотичної на цьому інтервалі.
називається вгнутою на інтервалі (a;b), якщо всі її точки, крім точки дотику, лежать вище довільної її дотичної на цьому інтервалі.
Точкою перегину називається така точка кривої, яка відділяє її опуклу частину від вгнутої .

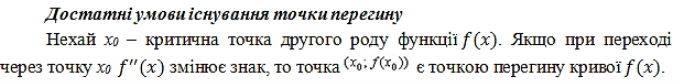
Приклад 3.
Знайти інтервали опуклості і вгнутості та точки перегину кривої ![]() .
.
Розв’язання
Знаходимо похідні
![]()
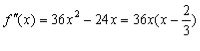
Розв’язуємо рівняння
![]()
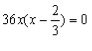
![]()
![]()

Асимптотою кривої ![]() називають пряму, до якої необмежено наближається точка кривої при необмеженому віддаленні її від початку координат.
називають пряму, до якої необмежено наближається точка кривої при необмеженому віддаленні її від початку координат.
Існує три типи асимптот: вертикальні, похилі та горизонтальні.
Пряма ![]() – вертикальна асимптота , якщо
– вертикальна асимптота , якщо
![]() або
або ![]() .
.
Пряма ![]() є похилою асимптотою, якщо існують скінченні границі
є похилою асимптотою, якщо існують скінченні границі
![]() (
(![]() ),
), ![]() .
.
При цьому зауважимо, що потрібно розглядати випадки як ![]() так і
так і ![]() .
.
Горизонтальною асимптотою графіка функції ![]() при
при ![]() називають пряму
називають пряму ![]() , коли
, коли
![]() (
(![]() ).
).
Зрозуміло, що горизонтальна асимптота є окремим випадком похилої асимптоти (![]() ).
).
- Загальна схема дослідження функції та побудова її графіка
Щоб дослідити функцію та побудувати її графік, треба:
1) знайти область існування (область визначення) функції;
2) знайти (якщо це можливо ) точки перетину графіка з осями координат;
3) дослідити функцію на періодичність, парність і непарність. Зауважимо, що графік парної функції симетричний відносно осі ординат, а графік непарної функції симетричний відносно початку координат;
4) знайти точки розриву та встановити їх характер;
5) за першою похідною знайти інтервали монотонності, точки локальних екстремумів та значення функції в цих точках;
6) за другою похідною знайти інтервали опуклості, вгнутості та точки перегину;
7) знайти асимптоти кривої;
8) дослідити поведінку функції в нескінченно віддалених точках;
9) обчислити в разі необхідності значення функції в кількох контрольних точках;
10) побудувати графік функції з врахуванням результатів попередніх пунктів.
Приклад 4
Дослідити функцію ![]() та побудувати її графік.
та побудувати її графік.
Розв’язання
1) Область існування – вся числова пряма, крім точки ![]() , тобто
, тобто ![]() .
.
2) Графік функції ![]() перетинає вісь ординат (якщо це можливо) в точці
перетинає вісь ординат (якщо це можливо) в точці ![]() . Знаходимо
. Знаходимо ![]() , отже
, отже ![]() – точка перетину кривої з віссю Oy. Щоб знайти точки перетину графіка з віссю Ox, потрібно розв’язати рівняння y=0, тобто
– точка перетину кривої з віссю Oy. Щоб знайти точки перетину графіка з віссю Ox, потрібно розв’язати рівняння y=0, тобто
![]() .
.
Це рівняння не має дійсних коренів, тому дана функція не перетинає вісь абсцис.
3) Функція неперіодична. Розглянемо вираз
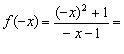
![]()
Таким чином, ![]() і
і ![]() . Це означає, що дана функція не є ні парною, ні непарною, тобто є функцією загального виду.
. Це означає, що дана функція не є ні парною, ні непарною, тобто є функцією загального виду.
4) Функція в точці х=1 має розрив другого роду, причому
![]() ,
, ![]() .
.
В усіх інших точках функція неперервна.
5) Знайдемо похідну
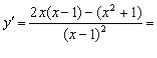
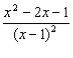
і розв’яжемо рівняння ![]() , тобто
, тобто
![]()
![]() ,
, ![]() – стаціонарні точки. Крім того, похідна невизначена при х=1. Отже,
– стаціонарні точки. Крім того, похідна невизначена при х=1. Отже, ![]() ,
, ![]() ,
, ![]() – критичні точки або точки можливого екстремуму. Ці точки розбивають числову пряму на чотири інтервали
– критичні точки або точки можливого екстремуму. Ці точки розбивають числову пряму на чотири інтервали
![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
На кожному з цих інтервалів похідна ![]() має певний знак, який можна встановити за методом інтервалів або обчислення значень похідної в окремих точках ( по одній точці з кожного інтервалу ). На інтервалах
має певний знак, який можна встановити за методом інтервалів або обчислення значень похідної в окремих точках ( по одній точці з кожного інтервалу ). На інтервалах ![]() ,
, ![]() похідна додатна, отже функція зростає; якщо
похідна додатна, отже функція зростає; якщо ![]() то функція спадає, бо на цих інтервалах похідна від’ємна. При переході через точку
то функція спадає, бо на цих інтервалах похідна від’ємна. При переході через точку ![]() ( рух відбувається зліва направо) похідна змінює знак з плюса на мінус, отже, в цій точці досягається локальний максимум, знайдемо
( рух відбувається зліва направо) похідна змінює знак з плюса на мінус, отже, в цій точці досягається локальний максимум, знайдемо
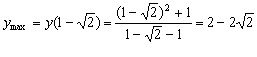 .
.
При переході через точку ![]() похідна змінює знак з мінуса на плюс, отже, в цій точці існує локальний мінімум, причому
похідна змінює знак з мінуса на плюс, отже, в цій точці існує локальний мінімум, причому
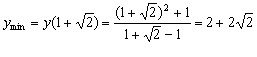 .
.
Точка x=1 не є точкою екстремуму ( в цій точці функція невизначена).
6) Знайдемо другу похідну
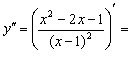
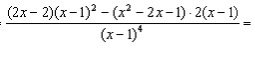
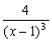 .
.
На інтервалі ![]()
![]() , отже, на цьому інтервалі крива опукла; якщо
, отже, на цьому інтервалі крива опукла; якщо ![]() , то
, то ![]() – крива вгнута. В точці x=1 функція невизначена, тому ця точка не є точкою перегину.
– крива вгнута. В точці x=1 функція невизначена, тому ця точка не є точкою перегину.
7) З результатів п.4 випливає, що пряма x=1 – вертикальна асимптота кривої.
Оскільки
![]() ,
, ![]() , то горизонтальні асимптоти відсутні.
, то горизонтальні асимптоти відсутні.
Знайдемо границі
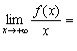
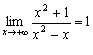 ,
, 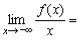
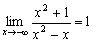 .
.
Отже, ![]() , тоді
, тоді
![]()
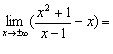
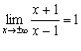 .
.
Таким чином, пряма ![]() – похила асимптота даної кривої. Інших асимптот немає.
– похила асимптота даної кривої. Інших асимптот немає.
8) Враховуючи проведені дослідження, будуємо графік.
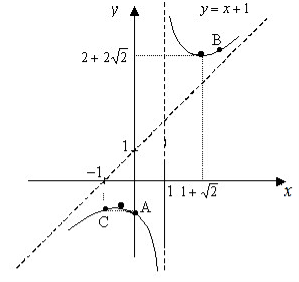
Що повинен знати та вміти студент
Знати необхідні та достатні умови монотонності функції, її локальних екстремумів.
Вміти знаходити інтервали монотонності, локальний та глобальний екстремум.
Вміти знаходити інтервали опуклості, точки перегину, асимптоти.
Вміти будувати графіки функцій за загальною схемою дослідження функцій.


про публікацію авторської розробки
Додати розробку