Знаходження диференціалів функцій. Наближені обчислення.

Дистанційне навчання

Дисципліна «ВИЩА МАТЕМАТИКА»

 

ПРАКТИЧНЕ ЗАНЯТТЯ

Тема: Знаходження диференціалів функцій. Наближені обчислення.

Мета: Сформувати вміння знаходити диференціали функцій, обчислювати наближено значення функцій за допомогою диференціала; застосовувати похідну та диференціал функції до розв’язування економічних задач.

Хід заняття

 

І. ПОВТОРІТЬ ТЕОРЕТИЧНИЙ МАТЕРІАЛ, ЯКИЙ ЗНАДОБИТЬСЯ ПРИ ВИКОНАННІ ЗАВДАНЬ:

 

1.1.Таблиця похідних деяких функцій.

1.2.Основні правила диференціювання

Теорема 1. Похідна сталої дорівнює нулю, тобто якщо у = с, де с = const, то y^/=0.

Теорема 2. Похідна алгебраїчної суми скінченої кількості диференційованих функцій дорівнює алгебраїчній сумі похідних цих функцій:

.

Теорема 3. Похідна добутку двох диференційовних функцій дорівнює добутку першого множника на похідну другого плюс добуток другого множника на похідну першого:

.

Теорема 4. Сталий множник можна виносити за знак похідної:

, де  .

Теорема 5. Якщо чисельник і знаменник дробу диференційовані функції (знаменник не перетворюється в нуль), то похідна дробу також дорівнює дробу, чисельник якого є різницею добутків знаменника на похідну чисельника і чисельника на похідну знаменника, а знаменник є квадратом знаменника початкового дробу

.

.

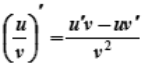1.3.Застосування диференціала в наближених обчисленнях:

.                (*)

Формула (*) дозволяє знаходити значення функції  в точці , якщо відомі значення  і , з точністю .

1.4. Застосування похідної та диференціала до розв’язування задач з економіки

Диференціальне числення дає змогу розв’язувати великий спектр задач економічного змісту, досліджувати економічні процеси, явища.

Продуктивність праці

ІІ.РОЗБЕРІТЬ РОЗВ’ЯЗАННЯ НАВЕДЕНИХ ПРИКЛАДІВ

 

2.1. Знаходження диференціалів функцій

 

Приклад 1. Знайти диференціал функції

Розв’язання. Знайдемо похідну за правилом похідної добутку функцій

та підставимо у формулу диференціалу

Ось і всі розрахунки

Приклад 2. Знайти диференціал функції

 

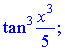
Розв’язання. Знаходимо похідну від тангенса, як від складеної функції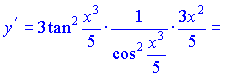

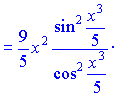
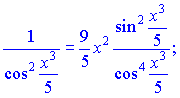
Обчислення непрості, спочатку беремо похідну від показника, далі від тангенса і вкінці від x³/5.
Записуємо диференціал функції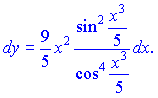

В знаменнику можна виділити квадрат косинуса і разом з чисельником записати як тангенс відповідного аргументу, а можна і залишити в такому вигляді.

Приклад 3. Знайти диференціал функції

Розв’язання. Диференціюємо арккосинус та підставляємо в формулу

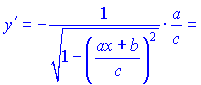
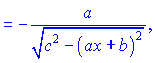
В результаті прийдемо до запису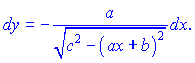
 

Приклад 4. Знайти диференціал функції

.

Розв’язання. Знаходимо похідну від заданої функції:

;

.

 

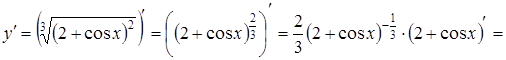
2.2. Наближені обчислення

Приклад 1. Наближено обчислити значення .

Розв’язання. В даному випадку , . Покладемо , що відповідає  в градусній мірі;

.

 

За формулою (*), отримаємо:

 

,

 

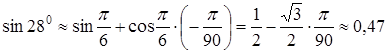тобто .

 

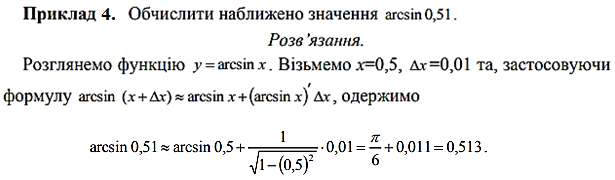
2.3. Застосування похідної та диференціала до розв’язування задач з економіки

 

 

Приклад 3. Залежність між витратами виробництва фірми С (умов. грош. од.) та обсягом випуску продукції х (од.) виражається функцією. Визначити середні й граничні витрати виробництва, якщо обсяг випуску продукції х=10 од.

Розв’язання.

Функція середніх витрат виражається формулою .

При х=10 середні витрати виробництва становлять (умов. грош. од.). Граничні витрати виробництва є похідна від функції витрат. При х=10 граничні витрати виробництва становлять (умов. грош. од.).

Отже, якщо, середні витрати виробництва становлять 45 умов. грош. од., то граничні витрати виробництва, тобто додаткові затрати на виготовлення додаткової одиниці продукції при даному рівні виробництва (обсяг випуску продукції х=10 од.), складають 35 умов. грош. од.

 

ІІІ.ВИКОНАЙТЕ ЗАВДАННЯ

(За варіантами! Викладач вказує прізвище і номер варіанта студента).

 

 

 

3. Розв’язати економічні задачі на застосування похідної та диференціала функції.

 

Варіант 1,4,7

А) Фірма реалізує свою продукцію за ціною р=40 умов. грош. од. за одиницю, а витрати виробництва при цьому визначаються функцією  . Знайти оптимальний для фірми обсяг випуску продукції та відповідальний йому прибуток.

Б) Залежність між витратами виробництва фірми С (умов. грош. од.) та обсягом випуску продукції х (од.) виражається функцією. Визначити середні й граничні витрати виробництва, якщо обсяг випуску продукції х=5 од.

 

Варіант 2,5,8

А) Фірма реалізує свою продукцію за ціною р=4 умов. грош. од. за одиницю, а витрати виробництва при цьому визначаються функцією  . Знайти оптимальний для фірми обсяг випуску продукції та відповідальний йому прибуток.

Б) Залежність між витратами виробництва фірми С (умов. грош. од.) та обсягом випуску продукції х (од.) виражається функцією. Визначити середні й граничні витрати виробництва, якщо обсяг випуску продукції х=10 од.

 

Варіант 3,6,9

А) Фірма реалізує свою продукцію за ціною р=28 умов. грош. од. за одиницю, а витрати виробництва при цьому визначаються функцією  . Знайти оптимальний для фірми обсяг випуску продукції та відповідальний йому прибуток.

Б) Залежність між витратами виробництва фірми С (умов. грош. од.) та обсягом випуску продукції х (од.) виражається функцією. Визначити середні й граничні витрати виробництва, якщо обсяг випуску продукції х=10 од.

 

Методичні вказівки до завдання А

Для знаходження оптимального для фірми обсягу випуску продукції обсяг продукції позначають змінною х і записують функцію прибутку фірми в разі виробництва х одиниць продукції:

,

де - доход від реалізації продукції, , де р – ціна за одиницю продукції.

Далі необхідно знайти похідну від функції прибутку та стаціонарні точки першого роду. Використовуючи теореми диференціального числення встановлюють, в якій зі стаціонарних точок функція прибутку буде мати максимум, це і буде оптимальний для фірми обсяг випуску продукції.

Щоб знайти прибуток, який відповідає оптимальному обсягу випуску продукції, отримане значення оптимального обсягу випуску продукції підставляють у функцію прибутку.

 

Методичні вказівки до завдання Б

Функція середніх витрат виражається формулою

.

Потім у функцію середніх витрат підставляють числове значення обсягу випуску продукції.

Граничні витрати виробництва є похідна від функції витрат

.

У функцію граничних витрат також  підставляють числове значення обсягу випуску продукції.

На підставі отриманих результатів роблять висновки.