Обернені тригонометричні функції
В моїй науково-дослідницькій роботі розглядаються обернені тригонометричні функції та приклади розв'язування завдань на обернені тригонометричні функції. Останнім часом на математичних олімпіадах пропонуються завдання на тригонометричні функції та обернені тригонометричні функції. Але ця тема не достатньо розглядається у курсі шкільної математики, тому школярам-учасникам математичних олімпіад потрібно самостійно опановувати елементи цього курсу математики.
Обернені тригонометричні функції також знайшли практичне застосування в інших точних науках. Наприклад, у шкільному курсі фізики при розв'язуванні задач на закони заломлення та відбивання світла.
Отже, моя науково-дослідницька робота буде корисною при підготовці до математичних олімпіад, а також зовнішнього незалежного оцінювання.
Обернені тригонометричні функції
Розвиток творчого потенціалу учнів шляхом удосконалення математичного мислення
Той, для кого двічі по два чотири – само собою
зрозуміле, ніколи не стане великим математиком.
Б. Брехт
Логіка розвитку сучасної цивілізації ставить перед освітою завдання, для виконання яких необхідно формулювати нові концептуальні ідеї навчання, що органічно поєднують елементи традицій та інновацій. Особливістю сучасності є те, що людина, щоб реалізуватися в суспільстві, повинна визначитися не стільки з тим, що вона знає і чого навчилася в школі, скільки зі здібностями і вміннями здобувати нові знання та використовувати їх у нових умовах. Отже, сучасному суспільству потрібна творча особистість. Тому у методичному банку сучасного вчителя поряд із традиційними формами повинні бути наявні й інноваційні технології. На мою думку, використання особистісно орієнтованих технологій дає можливість вчителю розвивати активну пізнавальну діяльність учнів. При такій системі навчання вчитель повинен бути не лише джерелом знань, а й компетентним консультантом і помічником учнів.
Особистісно зорієнтовані технології навчання передбачають по суті диференційований підхід до навчання з урахуванням рівня розвитку школяра, а також його підготовки з предмету, його здібностей і задатків. Серед технологій особистісно зорієнтованої педагогіки ключовими є технологія різнорівневого навчання, технологія інтерактивного навчання та проектна технологія. Я використовую саме ці технології з двох причин:
по–перше, в умовах класно–урочної системи вони найбільш легко вписуються у навчальний процес, дають змогу при інтеграції у реальний навчально – виховний процес досягти мети відповідно до будь – якої програми, стандартів освіти;
по–друге, вони гуманістичні, забезпечують не тільки успішне засвоєння навчального матеріалу всіма учнями, але й інтелектуальний і моральний розвиток дітей, їх самостійність, комунікабельність, бажання допомогти іншим. Це найбільш популярні у всіх розвинутих країнах світу технології, їх називають технологіями ХХІ ст.
Оскільки в кожному класі є діти з різним мисленням, увагою, властивістю пам’яті, то на деяких етапах уроку я використовую технологію різнорівневого навчання. Цей підхід ґрунтується на психолого–педагогічних відмінностях учнів. Учні умовно поділяються на групи, у залежності від досягнутого ними рівня підготовки. Учень може самостійно оцінити свої можливості і вибрати для себе той рівень, який відповідає його знанням на даний момент часу. Орієнтація на обов’язкові результати навчання постійно тримає підготовку учня на середньому рівні. Це дозволяє учневі при можливості перейти на більш високий рівень на будь – якому етапі навчання. Все це є гарантією оперативності, мобільності, гнучкості диференціації, створює в класі атмосферу взаємної довіри між вчителем і класом, дає можливості для розвитку творчої особистості.
Інтерактивне навчання – це спеціальна форма організації пізнавальної діяльності, яка має конкретну, передбачувану мету – створити комфортні умови навчання, за яких кожен учень відчує свою успішність, інтелектуальну спроможність. Суть інтерактивного навчання у тому, що навчальний процес відбувається за умови постійної, активної взаємодії всіх учнів. Це співнавчання, взаємонавчання (колективне, групове, навчання у співпраці), де учень і вчитель є рівноправними, рівнозначними суб’єктами навчання, розуміють, що вони роблять, рефлектують із приводу того, що вони знають, вміють і здійснюють. Організація інтерактивного навчання передбачає моделювання життєвих ситуацій, використання рольових ігор, спільне вирішення проблеми, аналіз обставин та відповідної ситуації. Воно ефективно сприяє формуванню навичок і вмінь, виробленню цінностей, створенню атмосфери співробітництва, взаємодії, дає змогу педагогу стати справжнім лідером дитячого колективу.
В інтерактивному навчанні не є визначальною форма роботи, а методи педагогічного впливу на пізнавально – навчальну діяльність учнів, на розвиток їх мислення, пізнання власних нахилів і здібностей. Груповій формі організації інтерактивного навчання повинні передувати індивідуальні інтерактивні підготовчі завдання, а самій роботі обов’язкова наявність спільної мети. Продукт індивідуальної праці використовується за роботи в групі для внесення коректив, змістовного доповнення, уточнення, вироблення спільної думки, формування висновків та інше. Тому у своїй діяльності на різних етапах уроку я практикую роботу дітей в парах, в групах та індивідуальну роботу. Колективна форма навчальної діяльності учнів – це форма організації навчання у малих групах учнів, об’єднаних спільною навчальною метою. Цей вид навчання відкриває для учнів можливості співпраці зі своїми ровесниками, дозволяє реалізувати природне прагнення людини до спілкування, сприяє досягненню учнями високих результатів засвоєння знань та формуванню вмінь. Коли діти навчаються разом з іншими у групі, вони відчувають істотну емоційну та інтелектуальну підтримку, яка дає їм можливість вийти далеко за рамки їхнього нинішнього рівня знань і вмінь. Така модель легко поєднується з традиційними формами і методами навчання і може застосовуватися на різних етапах навчання.
Співробітництво – спільна діяльність для досягнення загальних цілей. У межах спільної діяльності індивідууми прагнуть одержати результати, що є вигідними для них самих і для всіх інших членів групи. Ідея проста: одержавши інструкції від учителя, учні об’єднуються у невеликі групи. Потім вони виконують отримане завдання, поки всі члени групи не зрозуміють і не виконають його успішно. Спільні зусилля приводять до того, що усі члени групи прагнуть до взаємодії. У результаті виграють усі, успіхи кожного визначаються не тільки ними самими, а й зусиллями товаришів. Усі члени групи пишаються успіхами один одного і разом святкують перемогу.
Проектна технологія – це така організація навчання, за якої учні отримують знання у процесі планування та виконання практичних завдань. Метод проектів - це метод пошуку. Основні вимоги до даного методу:
- наявність проблеми (завдання), яка потребує інтегрованих знань, дослідницького пошуку для її вирішення;
- практична, теоретична, пізнавальна значущість запропонованих результатів;
- самостійна (індивідуальна, парна, групова) діяльність учнів;
- використання дослідницьких методів: визначення дослідницьких завдань, які випливають з обраної проблеми; висування гіпотези їх розв’язання, обговорення методів дослідження, оформлення результатів, аналіз отриманих даних, підбиття підсумків, коректування, висновки.
У своїй роботі я використовую різні типи проектів: дослідницькі, творчі, ігрові, інформаційні, практичні.
Використання цих технологій дозволяє різко збільшити відсоток засвоєння матеріалу, оскільки впливає не тільки на свідомість учня, а й на його почуття, волю. Дослідження, проведені сучасними психологами показали, що найменших результатів можна досягти за умов пасивного навчання, а найбільших – за умов інтерактивного навчання. За їхніми оцінками, школяр може, читаючи очима запам’ятати 10% інформації, слухаючи – 26%, розглядаючи – 30%, слухаючи і розглядаючи – 50%, обговорюючи – 70%, особистий досвід – 80%, спільна діяльність з обговоренням – 90%, навчання інших – 95%.
Отже, процес навчання потребує напруженої розумової праці дитини і її власної участі в усьому процесі. Стійких знань можна досягти тільки за умов активного навчання. Для підвищення активності, зацікавленості учнів до предмету, розвитку уваги, мислення, здібностей, творчості дітей у своїй роботі я використовую різні форми парної та колективної роботи, а саме: естафети, рольові ігри, шаради, ланцюгові вправи, конкурси команд: «спина до спини», «покажи на міміці», «загадковий кубик», «знайди відповідь», «розсипане твердження», «знайди зайве», «виправ мене», «правда, неправда» та інші.
Особистісно орієнтоване навчання має значні переваги над традиційним. Традиційна форма навчання орієнтована на наслідування, а активна – на перетворення самих себе у процесі різних способів взаємодії з учнями, вчителем. При цьому включення у сумісну діяльність відбувається з урахуванням індивідуального рівня розвитку кожної дитини. Таке навчання дозволяє сформувати в особистості вміння, навички самостійно вивчати певні явища, процеси, користуючись інформацією, вміння знаходити способи розв’язання проблеми, активно включатися у процес самостійної діяльності, працювати у колективі; виховує повагу, терпимість до іншої думки, толерантні стосунки між членами колективу.
Отже, така форма роботи дозволяє сформувати особистість, колектив. Саме у цих творчих колективах я організовую цікаві уроки та позакласні заходи. На уроках багато використовую задач практичного змісту. Це сприяє тому, що діти вчаться дивитися на деякі побутові проблеми поглядом людини, для якої математика є не сухою, абстрактною наукою, а потужним інструментом у розв’язанні деяких життєвих задач; і формує людину, яка може повністю застосувати вивчене на практиці. Часто в практиці я використовую нетрадиційні уроки: уроки-змагання, уроки-подорожі, урок-ділова гра, урок-КВК, інформаційно-дослідницькі проекти, інтегровані уроки, що значно підвищує інтерес учнів до вивчення математики.
В моїй науково-дослідницькій роботі розглядаються обернені тригонометричні функції та приклади розв’язування завдань на обернені тригонометричні функції. Останнім часом на математичних олімпіадах пропонуються завдання на тригонометричні функції та обернені тригонометричні функції. Але ця тема не достатньо розглядається у курсі шкільної математики, тому школярам-учасникам математичних олімпіад потрібно самостійно опановувати елементи цього курсу математики.
Обернені тригонометричні функції також знайшли практичне застосування в інших точних науках. Наприклад, у шкільному курсі фізики при розв’язуванні задач на закони заломлення та відбивання світла.
Отже, моя науково-дослідницька робота буде корисною при підготовці до математичних олімпіад, а також зовнішнього незалежного оцінювання.
Вступ.
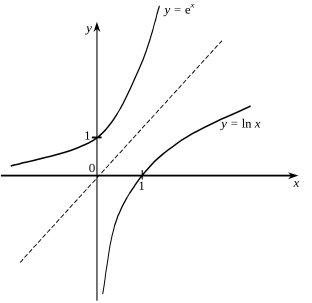
Нехай функція у = f(х) неперервна і монотонна на інтервалі (а,в) і при цьому змінна у набуває значень на інтервалі (с,d) . Розв’язавши рівняння у = f(х) відносно х, знайдемо розв’язок х = g(у).
Функція у= g(х) називається оберненою до функції у = f(х).
За зазначених умов обернена функція у= g(х) існує і неперервна при хє(с,d) . При цьому виконуються рівності:
g(f(х)) = х, хє(а,в); (1)
f(g(х)) = х, хє(с,d) .
Графіки функцій у = f(х) і у= g(х) симетричні відносно бісектриси першого координатного кута.
Наприклад, функція у = ![]() , -∞ < х < ∞, визначає залежність між змінними х і у, яку можна також подати рівнянням х =
, -∞ < х < ∞, визначає залежність між змінними х і у, яку можна також подати рівнянням х = ![]() , у > 0. Скориставшись позначеннями f(х) =
, у > 0. Скориставшись позначеннями f(х) = ![]() , g(х) =
, g(х) =![]() подамо рівності (1) у вигляді:
подамо рівності (1) у вигляді:
g(f(х)) = ![]() = х, -∞ < х < ∞, ; (2)
= х, -∞ < х < ∞, ; (2)
f(g(х)) = ![]() = х, х > 0.
= х, х > 0.
Графіки функцій у = ![]() , у =
, у =![]() симетричні відносно бісектриси першого координатного кута
симетричні відносно бісектриси першого координатного кута
(див. рисунок).
1. Графік і властивості функції y = arcsin x.
Функція у = ![]() неперервна і монотонна при х є
неперервна і монотонна при х є ![]() . Обернена до неї функція
. Обернена до неї функція
y = arcsin x , х є ![]() , називається арксинусом (див. рисунок).
, називається арксинусом (див. рисунок).
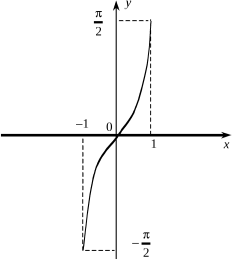
Функція y = arcsin x монотонно зростає на відрізку ![]() і задовольняє такі нерівності:
і задовольняє такі нерівності:![]() ≤ arcsin x
≤ arcsin x ![]() . (1)
. (1)
Арксинусом х (arcsin x) називається кут, що задовольняє нерівності (1) і синус якого дорівнює х:![]() ,
, ![]() . (2)
. (2)
Наведемо деякі числові значення функції arcsin x :![]() ;
; ![]() ;
; ![]() ; (3)
; (3)![]() ;
; ![]() .
.
Функція y = arcsin x — непарна, тобто![]() . (4)
. (4)
Корисно запам’ятати такі формули:![]() ,
, ![]() ;
;![]() ,
, ![]() ; (5)
; (5)![]() ,
, ![]() ;
;![]() ,
, ![]() ,
, ![]() .
.
2. Графік і властивості функції y = arccos x.
Функція y ![]() неперервна і монотонна при х є
неперервна і монотонна при х є ![]() . . Обернена до неї функція
. . Обернена до неї функція
y = arccos x , х є ![]() , називається арккосинусом (див. рисунок).
, називається арккосинусом (див. рисунок).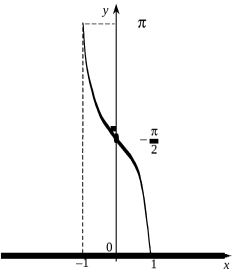
Функція y = arccos x монотонно спадає на відрізку ![]() і задовольняє такі нерівності:
і задовольняє такі нерівності:
0![]()
Арккосинусом x (arccos x) називається кут, що задовольняє нерівності (1) і косинус якого дорівнює х:![]()
![]() . (2)
. (2)
Із симетрії графіка відносно точки![]() випливає рівність:
випливає рівність:![]() ,
,
звідки знаходимо формулу![]() . (3)
. (3)
Порівнюючи графіки функцій y = arcsin x і y = arccos x , дістаємо:![]() ,
, ![]() . (4)
. (4)
Наведемо деякі числові значення arccos x :![]() ;
; ![]() ;
; ![]() ;
;![]() ;
; ![]() . (5)
. (5)
Корисно запам’ятати такі формули:![]() ,
, ![]() ;
;![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() . (6)
. (6)
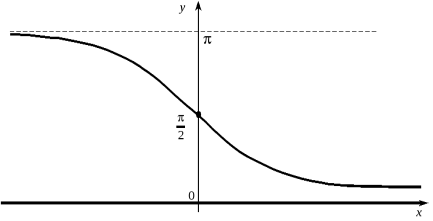
3. Графік і властивості функції y = arctg x.
Функція у = tg х неперервна і монотонна при х є ![]() . Обернена до неї функція
. Обернена до неї функція
y = arctg x , х є ![]() , називається арктангенсом (див. рисунок).
, називається арктангенсом (див. рисунок).

Функція y = arctg x монотонно зростає, непарна і задовольняє нерівності:![]() . (1)
. (1)
При цьому виконуються граничні співвідношення:![]() ,
, ![]() . (2)
. (2)
Арктангенсом x (![]()
![]() ,
, ![]() . (3)
. (3)
Функція y = arctg x набуває таких значень:![]() ,
, ![]() ,
, ![]() ; (4)
; (4)![]() ,
, ![]() .
.
Корисно запам’ятати деякі формули:![]() ;
; ![]() ,
,![]() ;
; ![]() , (5)
, (5)![]() ;
; ![]() ,
,![]() ;
; ![]() ,
, ![]() .
.
4. Графік і властивості функції y = arcctg x.
Функція у = сtg х неперервна і монотонна на проміжку![]() . Обернена до неї функція y = arcctg x, х є
. Обернена до неї функція y = arcctg x, х є ![]() , називається арккотангенсом (див. рисунок).
, називається арккотангенсом (див. рисунок).
Функція y = arcctg x монотонно спадає і задовольняє нерівності:![]()
При цьому виконуються граничні співвідношення:![]()
![]() . (2)
. (2)
Арксотангенсом x (arcctg x) називається кут, що задовольняє нерівності (1) і котангенс якого дорівнює х:![]() ,
, ![]() . (3)
. (3)
Розглядаючи графіки арктангенса і арккотангенса, доходимо висновку, що завжди виконуються рівності:![]() ; (4)
; (4)![]() . (5)
. (5)
Наведемо табличні значення арккотангенса:![]() ;
; ![]() ;
; ![]() ;
;![]() ;
; ![]() . (6)
. (6)
Корисно запам’ятати такі формули:![]() ,
, ![]() ,
,![]() ,
, ![]() , (7)
, (7)![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() .
.
5. Співвідношення другого роду між аркфункціями.
Спочатку розглянемо пару аркфункцій, значення яких знаходяться в однакових межах, а саме візьмемо arcsin x і arctg x. Зачення обох цих функцій знаходяться у проміжку від -![]() до
до ![]() , на цьому проміжку дуга визначена, якщо дано зачення її синуса чи тангенса. Нехай у = arcsin x , тоді
, на цьому проміжку дуга визначена, якщо дано зачення її синуса чи тангенса. Нехай у = arcsin x , тоді
tg(arcsin x) =![]() , ( х ≠ -1;1) (1),
, ( х ≠ -1;1) (1),
Дуга arctg ![]() , за визначенням арктангенса, має тангенс, що дорівнює
, за визначенням арктангенса, має тангенс, що дорівнює ![]() і розташована в проміжку
і розташована в проміжку ![]() .
.
Враховуючи рівність (1), дуга arcsin x має такий же тангенс і розташована в тому ж інтервалі ![]() . Звідки отримаємо рівність:
. Звідки отримаємо рівність:
arcsin x = arctg ![]() , (
, ( ![]() < 1) . (2)
< 1) . (2)
Рівність (2) випливає з формули елементарної тригонометрії, що виражає тангенс через синус.
Таким же чином з рівності
![]() arctg x) =
arctg x) = ![]()
випливає рівність
arctg x = arcsin ![]() . (3)
. (3)
Аналогічно виконується перетворення арккосинуск в арккотангенс. На проміжку ( 0; ![]()
![]() arсctg x) =
arсctg x) = ![]() і сtg(arccos x) =
і сtg(arccos x) = ![]()
випливають рівності:
![]()
![]() і arccos x =
і arccos x = ![]() . (4)
. (4)
Інакше перетворюються одна в іншу аркфункції, значення яких розташовуються в різних проміжках. Розглянемо перетворення функції у = arcsin x у арккосинус.
Для значень 0 ≤ х ≤1 маємо 0 ≤ arcsin x ≤ ![]() .
.
Дуга у має косинус, що дорівнює ![]() і тому
і тому
arcsin x = arccos ![]() .
.
Якщо -1 ≤ х ≤ 0, то ![]() 0, для функції arccos
0, для функції arccos ![]() маємо 0 ≤ arccos
маємо 0 ≤ arccos ![]() ≤ π.
≤ π.
Звідси видно,що при від’ємних значеннях х написана вище рівність виконуватися не може, оскільки дуги arcsin x і arccos ![]() розташовані в різних проміжках. Дійсно, при від’ємних значеннях х дуга arcsin x міститься в четвертій чверті, дуга arccos
розташовані в різних проміжках. Дійсно, при від’ємних значеннях х дуга arcsin x міститься в четвертій чверті, дуга arccos ![]() - в першій чверті, оскільки аргумент арккосинуса є арифметичний квадратний корінь, отже число додатне.
- в першій чверті, оскільки аргумент арккосинуса є арифметичний квадратний корінь, отже число додатне.
Розташування цих дуг пояснюється малюнком:
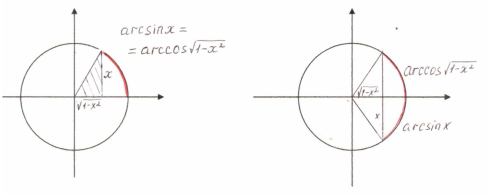
При від’ємних значеннях х маємо: х < 0, звідки –х > 0 і
![]()
![]()
![]() .
.
Таким чином:
![]()
![]() (5)
(5)
Розглянемо функцію у = arccos ![]() . Областю її визначення є проміжок
. Областю її визначення є проміжок ![]() . Відповідно до рівності (5) закон відповідності можна записати у вигляді:
. Відповідно до рівності (5) закон відповідності можна записати у вигляді:
arccos ![]() =
= ![]()
Аналогічно, якщо х ≥ 0, маємо:
arccos х = ![]() ,
,
якщо -1 ≤ х ≤ 0, то
arccos х = π – arccos(- х) = π - ![]() .
.
Отже,
arccos х = ![]() (6)
(6)
Із співвідношення ![]() arctg x) =
arctg x) = ![]() якщо х ≥ 0 маємо:
якщо х ≥ 0 маємо:
arctg x = arccos ![]() ,
,
якщо х< 0, то
arctg x = - arctg(- x) = - arccos ![]() .
.
Таким чином,
arctg x = 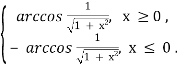
Аналогічно, якщо 0 < х ≤ 1, то
arccos х = arctg![]() ,
,
якщо ![]()
arccos х = π – arctg![]() ) = π + arctg
) = π + arctg![]() .
.
Отже,
arccos х = 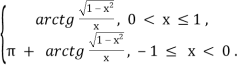
Аналогічно отримаємо рівності:
arctg x = 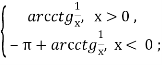
![]()
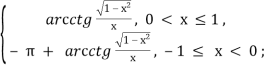
arсctg x =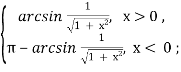
arсctg x =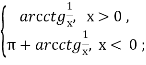
6. Приклади
- Перевірити справедливість рівностей:
а) ![]()
![]()
Розв’язання:
![]() =
=![]()
![]() =
= ![]() ∙
∙ ![]() -
- ![]()
![]() = =
= = ![]() .
.
Отже, ![]()
![]() .
.
б) tg( 2arcsin x ) = ![]()
Розв’язання:
tg( 2arcsin x ) = ![]() =
= ![]() =
= ![]() =
= ![]() .
.
Отже, tg( 2arcsin x ) = ![]() .
.
в) tg( arcsin x - ![]()
![]()
Розв’язання:
tg( arcsin x – ![]()
![]()
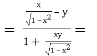
![]() .
.
Отже, tg( arcsin x - ![]()
![]() .
.
г) ![]() - arcsin
- arcsin ![]() ) = 2
) = 2![]()
Розв’язання:
![]() - arcsin
- arcsin ![]() ) =
) = ![]() ) ∙
) ∙![]()
![]() )+ +
)+ + ![]() ) ∙
) ∙ ![]() =
=
= ![]() ∙
∙![]() +
+ ![]() =
=
= ![]() ∙
∙ ![]() = 2
= 2![]() .
.
Отже, ![]() - arcsin
- arcsin ![]() ) = 2
) = 2![]() .
.
д) ![]() ) =
) =![]()
Розв’язання:
![]()
+ ![]() +
+
+![]() =
=![]() .
.
Отже, ![]() ) =
) =![]() .
.
- Довести, що х + у + z = xyz за умови
![]()
Доведення:
Скористаємося формулою: tg( α + β + γ ) = ![]() .
.
Згідно з умовою маємо: tg(![]()
Тоді ![]() = 0, отже х + у + z = xyz, що і треба було довести.
= 0, отже х + у + z = xyz, що і треба було довести.
-
Показати, що сtg(
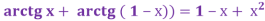 .
.
Доведення:
сtg(![]() =
= ![]() =
=
=![]() .
.
Отже, сtg(![]() .
.
- Записати у вигляді многочлена:
а)![]() )
)
Розв’язання:
![]() ) =
) = ![]() +
+ ![]()
=![]() )
)![]() )–
)– ![]() х ∙ ( 2
х ∙ ( 2![]() ) – 1) –
) – 1) –
![]() ∙ 2
∙ 2![]() х ∙ ( 2х2 – 1 ) –
х ∙ ( 2х2 – 1 ) –
![]() ∙ 2 ∙
∙ 2 ∙![]() ∙ х = 2х3 – х - ( 1 – х2 ) ∙ 2х = 2х3 – х – 2х +
∙ х = 2х3 – х - ( 1 – х2 ) ∙ 2х = 2х3 – х – 2х +
+ 2х3 = 4х3 – 3х.
б) ![]()
Розв’язання:
![]() = 2
= 2![]() ) – 1 = 2( 2
) – 1 = 2( 2![]() ) – 1)2 – - 1 = 2( 2х2 – 1 )2 - 1 = 2( 4х4 – 4х2 + 1) -1 = 8х4 – 8х2 + 1.
) – 1)2 – - 1 = 2( 2х2 – 1 )2 - 1 = 2( 4х4 – 4х2 + 1) -1 = 8х4 – 8х2 + 1.
- Записати у вигляді алгебраїчних функцій:
а) tg(![]()
Розв’язання:
tg(![]()
![]()
![]() =
=
=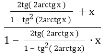 =
= ![]() =
=
=  =
= 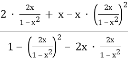 =
=
= 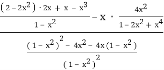 =
= ![]() =
=
=![]() =
= ![]() =
= ![]() .
.
б) ![]()
Розв’язання:
![]() = 2
= 2![]() cos
cos![]() =
=
= 2∙ (2![]() ∙cos
∙cos![]() ) ∙(
) ∙(![]() -
- ![]() ) =
) =
= 2(2х![]() )((1 -
)((1 - ![]() ) -
) - ![]() ) = 4х
) = 4х![]() ∙ (1 - 2
∙ (1 - 2![]() ).
).
в)![]()
![]()
Розв’язання:
![]()
![]()
![]()
= ![]()
![]()
![]()
![]()
![]()
![]() ∙
∙ ![]()
![]()
![]()
![]() ) –
) –
- 1 ) ∙ ![]() =
= ![]() ∙
∙ ![]() ∙
∙ ![]() +
+ ![]() =
=
= ![]() +
+ ![]() =
= ![]() .
.
-
Довести, що

 =
= 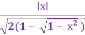 .
.
Доведення:
![]()
![]() =
= ![]() =
= ![]() =
= ![]() = =
= = ![]() .
.
( в чисельнику записуємо ![]()
![]()
![]() > 0 ).
> 0 ).
Отже, ![]()
![]() =
= ![]() , що і треба було довести.
, що і треба було довести.
-
Довести, що

 =
= 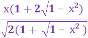 .
.
Доведення:
![]()
![]()
![]()
![]()
![]() + ( 1 –
+ ( 1 –
- 2![]() = 2
= 2![]()
![]() ) +
) + ![]()
![]() ) = 3
) = 3![]()
![]() ;
;
![]()
![]() =
= ![]()
![]() – 4
– 4![]()
![]() - 4 ∙
- 4 ∙ ![]() - -
- - ![]() =
= ![]() ∙ ( 3 – 1 +
∙ ( 3 – 1 + ![]() ) =
) =
= ![]() ∙ ( 2 +
∙ ( 2 + ![]() ) =
) = ![]() (2 +
(2 +![]() ) =
) =
![]() .
.
Отже, ![]()
![]() =
= ![]() , що і треба було довести.
, що і треба було довести.
-
Показати, що
 =
= 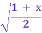 ∙ (2х - 1).
∙ (2х - 1).
Доведення:
![]()
![]()
![]()
![]() -
- ![]()
![]() ∙
∙![]()
= 2![]() –
– ![]()
![]()
![]() ) = 2
) = 2![]() –
– ![]()
![]()
![]() = 4
= 4![]() –3
–3![]()
![]() = 4 ∙
= 4 ∙![]() 3 ∙
3 ∙ ![]() =
=
= 4 ∙ ![]() - 3 ∙
- 3 ∙ ![]() =
= ![]() ∙
∙ ![]() =
= ![]() ∙ (2х - - 1).
∙ (2х - - 1).
Отже, ![]() =
= ![]() ∙ (2х - 1).
∙ (2х - 1).
-
Довести рівність tg(
 =
= 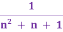 .
.
Доведення:
tg(![]() =
= =
= ![]() =
=
= ![]() =
= ![]() .
.
Отже, tg(![]() =
= ![]() , що і треба було довести.
, що і треба було довести.
- Обчислити:
а) 2![]()
![]()
![]()
Розв’язання:
2![]()
![]() =
= ![]() + π +
+ π + ![]() = π
= π ![]() +
+
+ 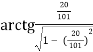 = π +
= π + ![]()
![]() = π .
= π .
б) 4![]()
![]()
Розв’язання:
4![]()
![]() = 2
= 2![]()
![]() = 2
= 2![]()
![]() = 2
= 2![]()
![]() =
= ![]() =
=
= ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]() =
= ![]()
11. Довести:
а) ![]() х =
х = ![]()
Доведення:
Зазначимо, що ![]() <
< ![]() , оскільки ∣х∣ ≤ 1 ,
, оскільки ∣х∣ ≤ 1 ,
![]() = 2 ∙
= 2 ∙ ![]() ∙
∙ ![]() =
=
= ![]() =
=
= ![]() =
= ![]() =
=
= ![]() =
= ![]()
Отже, ![]() х =
х = ![]() , що і треба було довести.
, що і треба було довести.
б) ![]() х =
х = ![]()
Доведення:
Оскільки ![]() , то
, то ![]() < 1.
< 1.
![]() = 2 ∙
= 2 ∙ ![]() ∙
∙ ![]() =
= ![]()
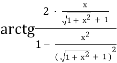 =
=
=![]()
![]()
![]() =
=
= ![]()
![]() =
= ![]()
![]() =
=
= ![]() х.
х.
Отже, ![]() х =
х = ![]() , що і треба було довести.
, що і треба було довести.
в) ![]() =
=![]()
Доведення:
![]() =
= ![]() =
= ![]()
![]() =
= ![]() ,
,
зазначимо, що 0 ≤ ![]() ≤ 1, оскільки ∣х∣ ≤ 1.
≤ 1, оскільки ∣х∣ ≤ 1.
Отже, ![]() =
=![]() , що і треба було довести.
, що і треба було довести.
г) 2![]()
![]()
Доведення:
4![]() = 4
= 4![]() = 4
= 4![]() = 2π –
= 2π –
![]()
![]() = π +2
= π +2![]()
Отже, 2![]()
![]() , що і треба було довести.
, що і треба було довести.
12. Обчислити:
а) ![]()
Розв’язання:
![]()
![]() = 0.
= 0.
б) ![]()
Розв’язання:
![]()
![]() =
= ![]() = 0,6.
= 0,6.
в) ![]()
Розв’язання:
![]() ) = 2
) = 2![]() )
)![]() ) = 2
) = 2![]() ∙
∙ ![]() = =
= = ![]() ∙
∙ ![]() =
= ![]() .
.
7. Вправи для самостійногорозв’язування.
- Обчислити:
-
tg (
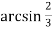 ) ;
) ;
-
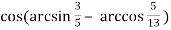 ;
;
-
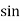
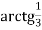 ) ;
) ;
-
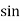
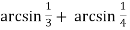 ) ;
) ;
-
tg (2
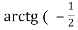 ) ) ;
) ) ;
-
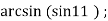
-
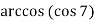 ;
;
-
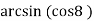 ;
;
-
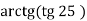 ;
;
![]() ;
;
11)![]() .
.
- Довести:
-
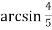 =
= 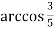 =
= 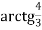 =
= 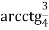 ;
;
-
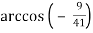 = π
= π 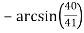 ;
;
-
 =
= 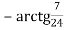 ;
;
-
2
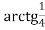 +
+ 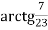 =
=  ;
;
-
π
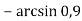
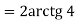
-
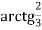 +
+ 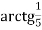 =
=  ;
;
-
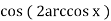
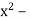 1, де ∣х∣ ≤ 1;
1, де ∣х∣ ≤ 1;
-
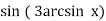 = 3х – 4х3, де ∣х∣ ≤ 1;
= 3х – 4х3, де ∣х∣ ≤ 1;
-
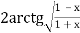 =
= 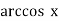 ;
;
-
3
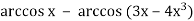 = π
= π
-
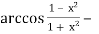 2
2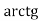
- Обчислити суму:
-
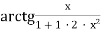 +
+  + … +
+ … + 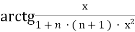 ;
;
-
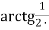 +
+ 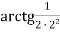 + …
+ … 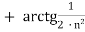 .
.
- Розв’язати рівняння:
-
6
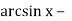 π = 0;
π = 0;
-
2
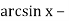 8 =0;
8 =0;
-
3
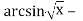 π = 0;
π = 0;
-
4
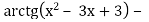 π = 0;
π = 0;
-
2
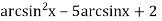 = 0;
= 0;
-
4
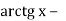
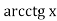
-
π
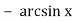 =
= 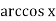
-
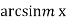 =
= 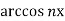
-
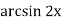 =
=  .
.
Список використаної літератури
- Векселев В.Я. Факультативные курсы завоевали прочные позиции.
„ Математика в школе ”, 1971, № 6.
- Епишева О.Б. Некоторые методические приемы проведения факультативних занятий. „ Математика в школе ”, 1968, №4.
- Фирсов В.В., Боковнев О.А. Состояние и перспективы факультативних занятий по математике. Москва, 1977.
- Методика факультативних занятий в 7 – 8, 9 – 10 классах. Москва, 1981.
- Методический сборник по математике. Материалы для факультативних и внеклассных занятий. Калининград, 1981.
- Сорник задач по математике /для факультативних занятий/. Москва, 1971.
- Фридман Л.М. Психолого – педагогические основы обучения математике в школе. Москва, Просвещение, 1983.
- Бевз Г.П. Методика преподавания математики. Киев, Вища школа, 1989.
- Кадыров И.И. Взаимосвязь внеклассных и факультативних занятий по математике . Москва, Просвещение, 1983.
- Мавашев Д.А. Внеклассная работа по математике. Ташкент, Укитувчи, 1989.
- Алгебра и начала анализа в 9 – 10 классах. Москва, Просвещение, 1980.
- Алгебра и начала анализа в 9 – 10 классах. Пособие для учителей. Москва, Просвещение, 1982.
- Новоселов С.И. Оратные тригонометрические функции. Москва, Учпедгиз, 1950.
- Новоселов С.И. Специальный курс тригонометрии. Москва, Высшая школа, 1967.
- Виноградова И.А., Олехник С.Н., Садовский В.А. Задачи и упражнения по математическому анализу. Москва, Издательство Московского университета, 1988.
- Литвиненко В.Н., Мордкович А.Г. Практикум по элементарной математике. Алгебра. Тригонометрия. Москва, Просвещение, 1991.


про публікацію авторської розробки
Додати розробку
