Стаття на тему: " Використання прикладних задач при викладанні математики".

С. О. Сафонюк,

учитель математики, вища кваліфікаційна категорія, старший учитель

ЗОШ № 7 ім. В. В. Бражевського

 м. Житомир

Використання прикладних задач при викладанні математики

   Для оволодіння та управління сучасною технікою та технологіями необхідна ґрунтовна загальноосвітня підготовка, яка містить в якості обов’язкового компонента активні знання з математики.

   Наявність знань ще не передбачає те, що вони є тим запасом, який дозволить учням застосовувати їх у різноманітних реальних ситуаціях. Така здібність не може з’явитись стихійно. Подібний рівень математичної підготовки досягається в процесі навчання, яке зорієнтоване на широке розкриття зв’язків математики з навколишнім середовищем.

   Зв’язок викладання математики з оточуючим середовищем є дійсним засобом реалізації одного з найважливіших принципів педагогіки – єдності теорії та практики. Все це допомагає учням зрозуміти життєву необхідність знань, які вони набувають в школі. В цьому і полягає виховне значення такого навчання.

   Сутність задач з практичним змістом та вимоги до таких задач.

 Під задачею прикладного характеру потрібно розуміти таку, що розкриває застосування математики в інших навчальних дисциплінах, знайомить з її використанням в навколишньому світі, формує свідомого громадянина України.

   До задач з практичним змістом наряду із загальними вимогами необхідно додати додаткові. А саме:

1) пізнавальна цінність задачі та її виховна сутність;

2) доступність учням нематематичного матеріалу, який використовується;

3) реальність ситуацій, числових даних, поставлених питань та отриманої відповіді.

   На разі в діючих підручниках присутні задачі, які автори намагаються представити, як практичні, де не виконуються вимоги, про які говорилось вище. В результаті в учнів складається невірна уява про процеси, явища, факти та історичні або побутові ситуації. Не буду говорити про конкретні підручники ( кожен творчо працюючий вчитель може сам навести приклади ) та хотілось би навести один приклад такої задачі: « Котигорошко може нарубати 300 м³ дров за 3 хв, а Івасик-Телесик ту саму кількість дров – за 6 хв. За скільки вони разом можуть нарубати стільки дров? » Думається, що тут можна зробити певний висновок.

   Подібні приклади не поодинокі. Тому необхідне більш критичне відношення учителя до запропонованих в підручниках та навчальних посібниках задач з практичним змістом. В деяких випадках учителю потрібно виправляти допущені погрішності, а в інших – давати відповідні пояснення.

   Зрозуміло, що жоден підручник не може розкрити всі різноманітні зв’язки шкільного курсу математики з іншими навчаль, ними дисциплінами. Тому доречним буде учителю самостійно доповнювати запропоновані в підручниках системи вправ задачами, які він склав самостійно чи разом з учнями. З особистої практики хочу зауважити, що учням подобаються такі задачі, і вони залюбки намагаються придумати свої.

   Використання задач з практичним змістом на уроках математики.

1. Мотивація учнів для вивчення нового матеріалу.

   Використання таких задач як засіб мотивації знань, вмінь та навичок створює чудові умови для реалізації під час вивчення нового матеріалу зв’язку математичного матеріалу з середовищем, що нас оточує та іншими навчальними предметами.

   Якщо перед вивченням нового теоретичного матеріалу запропонувати одну-дві задачі – це дасть чудові можливості для використання на уроках математики елементів проблемного навчання. Важливість задач проблемного характеру для досягнення мети та цілей вивчення математики переоцінити неможливо. Їх використання забезпечує більш свідоме вивчення теорії, навчає  учнів самостійності, засобам пошуку, дослідження та доведення, вмінню виділяти математичні об’єкти.

   Задачі повинні бути підібрані таким

чином, щоб їх завдання спонукало учнів до необхідності отримання нових знань, а вже отримані через цю необхідність знання дозволяли розв’язати не тільки дані задачі, але і інші прикладні задачі. Для створення проблемної ситуації можна використати не тільки цілу задачу (причому не потрібно її розв’язувати), але і будь-які фрагменти. А вже в цілому задачі розв’язуються при закріпленні знань учнів.

Приклади

1.1. При введені понять про вписані  многокутники в коло можна розглянути наступну проблемну задачу: «Як знайти центр квітника, якщо він круглої форми?»

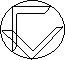Розв’язування:

Крок 1:  вписати 2 прямих кути

в коло.

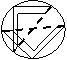Крок 2: через точки перетину

сторін кутів з колом провести 2

 прямі.

Відповідь: точка перетину прямих

                  і буде центром кола.

В учнів виникає питання «чому?», що буде гарним стимулятором для вивчення даної теми.

1.2.^* Перед початком ознайомлення учнів з геометричною прогресією пропоную задати учням задачу-жарт: «Один з учнів, викликаний до дошки, повинен йти від свого місця до столу вчителя по прямій. 1-й крок  він робить довжиною 1 м, 2-й – 1/2 м, 3-й – 1/4 м і т.д., тобто кожний наступний крок у 2 рази менше від попереднього.  Через який час дійте учень до столу вчителя, якщо відстань від парти до столу по прямій 3 м?»

Відповідь: учень не зможе дійти до столу учителя, а «чому?», ми з вами дізнаємось коли розглянемо нашу тему.

^*Примітка. Розв’язки цієї та деяких інших задач будуть подані нижче.

1.3^* При розгляді питання про застосування похідної можна запропонувати учням на уроці технологій з квадратного листа заданих розмірів зробити коробочку найбільшого об’єму.

   Таким чином учні впевнюються у практичній необхідності нових знань. Це спонукає їх до більш уважнішого та детальнішого вивчення навчального матеріалу.

   Тут учителю можна особливо підкреслити, що отримавши та оволодівши новими поняттями, учні зможуть розв’язувати не тільки ці задачі, а й інші прикладні завдання.

2. Наочність навчального матеріалу.

   Приклади з оточуючого нас середовища дозволяють розкривати перед учнями практичне значення математики, багатогранну можливість її застосовувати. Ці приклади повинні бути переконливими і доступними для розуміння учнями.

   Особливо необхідно звернути увагу на те, що багаточисленні закономірності явищ, з якими ми стикаємось у повсякденному житті, є конкретними моделями загальних математичних співвідношень. Так пряму пропорційність, яка задається формулою , можна проілюстровати залежністю між довжиною кола та її діаметром (), між кількістю зробленої роботи А та часом t  при сталій продуктивності праці ().

   Немаловажну роль у вивченні математики відіграють вміння учнів виконувати проектні завдання та подальший їх захист. Це спонукає школярів до самостійної роботи при знаходженні певного матеріалу, до творчого підходу вирішення практичного завдання та обґрунтованого, послідовного і логічного доведення його до аудиторії.

Приклади

2.1. Під час вивчення теми: «Вписані в коло многокутники» можна поставити творче завдання, яке виходить за рамки шкільного підручника.

Питання. Як з підручних засобів зробити правильний п'ятикутник і вписати його в коло?

Відповідь. Візьміть прямокутну стрічку паперу та зробіть вузол, який за формою дає правильний п'ятикутник.

Щоб вписати п'ятикутник в коло зробимо наступні кроки:

1) проведемо серединні перпендикуляри до його сторін (досить трьох) – це буде центр описаного (вписаного) кола;

2) сумістимо центр п'ятикутника з центром кола так, щоб одна його сторона була паралельна до діаметра кола;

3) продовжимо побудовані перпендикуляри до перетину з колом і проведемо пряму через сторону, яка паралельна до діаметра кола – отримаємо 5 точок;

 

4) з'єднаємо ці точки –

отримали шуканий п'ятикутник.

 

2.2. Під час вивчення теми: «Множини. Дії з множинами» можна запропонувати учням самім скласти задачу та знайти її розв’язок.

Наприклад. В  козацькому загоні із 220 чоловік за отамана Вернидуба згодні проголосувати 173 козака, а за отамана Крутивуса – 128 козаків. Скільки козаків остаточно не визначилось зі своїм вибором?

Розв’язування.     Нехай є три множини: А – {вибирають Вернидуба}, В – {вибирають Крутивуса}, С – {всього козаків}. Потрібно знайти  множину  Е – {козаки, що лояльні до обох}. Тоді n(A) = 173, n(B) = 128, n(AB) = n(C) = 220. Водночас AB = E. Використовуючи формулу для скінчених множин та те, що Е , маємо:

 n(E) = n(A) + n(B) - n(AB) = 173+128-

-220=81. Отже, козаків, серед яких можна проводити агітацію -  81.

Відповідь: 81 козак.

2.3. Задача на обернену пропорційність.

Загін з 60 козаків може побудувати «чайку» за 12 днів. За який час таку саму роботу виконають 80 козаків.

Розв’язування.      Нехай 80 козаків побудують “чайку” за х днів. Складемо скорочену умову задачі.  

   60 козаків – 12 днів  Із збільшенням числа

   80 козаків – х днів     козаків зменшується

                                       кількість днів.

   Складемо пропорцію:

  

   Відповідь: 9 днів.

Такі задачі як 2.2 і 2.3 цікаві ще тим, що виховують в учнів любов і повагу до історії рідної країни, до створення учнями математичних моделей певних реальних подій ( в даному випадку – історичних ).

   Велику пізнавальну цінність містить виконання вправ, пов’язаних з виділенням на реальних предметах, їх моделях або зображеннях знайомих геометричних фігур. Це можна застосовувати, наприклад, при вивченні теми: «Розв’язування трикутників».

2.4. Від західного купола до центрального входу (АС)  відстань дорівнює 93м, а до східного купола (АВ) відстань дорівнює 65м, кут між цими сторонами дорівнює  42⁰. Знайти відстань від східного купола до центрального входу ( ВС ).

 Дано: ∆ АВС

 АС = 93 м,

 АВ = 65 м,

Знайти: ВС

Розв’язання. ∆АВС. За теоремою косинусів знайдемо сторону ВС.

(м). Відповідь: 62 м

2.5. В двох пунктах А і В, відстань між якими 100 м, отримали сигнал про допомогу з пункту D. З цих пунктів в пункт С, де знаходиться команда рятівників були відправлені сигнали – накази про надання допомоги. Як знайти відстань, яку повинні пройти рятівники з пункту С до пункту D, якщо відомі кути між напрямами сигналів?

Збудуємо геометричну модель задачі.

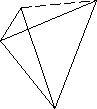     C                     D       Дано:  АВ = 100 м

         О                 

А                            

                              Знайти: CD

                           Розв’язання.

                       1. 

         B               

       

За теоремою синусів:   

= (м)

2.

За теоремою синусів:

125 (м)

3.

За теоремою косинусів:

CD =

CD =

CD 179,3 (м ).    Відповідь: 179,3 м

   Така робота сприяє розвитку просторової уяви  учнів, розширенню їх кругозору та є ефективним засобом наочності зв’язку навчання з життям. Використання мультимедійних презентацій дозволяє такі завдання робити  привабливими та зрозумілими.

3. Закріплення та поглиблення знань  

   Форми використання  задач з практичним змістом для закріплення та поглиблення знань в учнів з математики бувають різноманітними. Ці задачі можуть використовуватись і в роботі з усім класом, і для індивідуальної або групової роботи з окремими учнями, і в якості творчих завдань для школярів, які проявляють інтерес до математики та її прикладному характеру.

3.1. Задачі, розв’язок яких зорієнтовано на пряме застосування матеріалу, що вивчається з математики

3.1.1. Знайдіть об’єм піраміди Хеопса, площа основи якої 5,3 га, а висота – 147 м.

                                           Розв’язування

                                       1 га = 10000 м², тоді

                                       5,3 га = 53000 м².

                                      

                                     

                                      ( м³ )

                                    Відповідь: 2597000 м³

3.1.2. Переріз залізничного насипу має вигляд трапеції з нижньою основою 18 м, верхньою 8 м і висотою 3 м. Знайдіть об’єм такого насипу довжина  в 1 км.

Задача цікава тим, що не всі учні, навіть 11-го класу, можуть уявити собі цю насип. Тому мультимедійна презентація цієї задачі та її розв’язання повинна зацікавити  Представимо цей насип у вигляді прямої призми, в основі якої лежить трапеція з основами 8 м і 18 м та висотою 3 м. Висота призми 1000 м. Знайдемо об’єм цієї фігури.

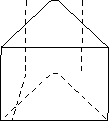    В₁                С₁    Дано: ABCDA₁B₁C₁D₁ –

                                        пряма призма

                                 AD = 18 м, BC = 8 м,

А₁                           D₁            АА₁ = 1000 м

       В                С        ВК – висота, ВК = 3 м

                              Знайти: V

А К                        D   

Розв’язування:   

 

( м³ )

 Відповідь: 39000 м³

3.1.3 Знайти висоту маяка, підхід до якого перегороджує річка.

На практиці це виконують так: відмічають дві точки на горизонтальній прямій, яка

проходить через основу маяка; в кожній точці за допомогою теодоліта визначають кут, під яким видно верхівку об’єкта; проводять відповідні обчислення.

Складемо умову даної задачі, зробимо рисунок та проведемо розрахунки.

З двох точок А і С, відстань між якими 12 м, вершину маяка видно під кутами 42⁰ та 37⁰

відповідно. Висота приладу над землею  –

 h = 1,5 м. Знайти висоту маяка.

Для того, щоб учні зрозуміли задачу можна в якості рисунка запропонувати наступний мультимедійний слайд, де на картинці з маяком побудована її геометрична модель.

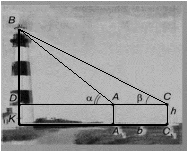                                                   Дано: ΔАВС

                                                   ,

                                                   ,

                                                    AC = 12 м,

                                                    AA₁ = CC₁ =

                                                     = h = 1,5 м

                                                    Знайти: КВ

 

Розв’язування                                  

(властивість зовнішнього кута).За теоремою синусів маємо:        (м)

Δ BDA ().

(м).

ВК = BD + DK = 55,4 + 1,5 57 (м).

Відповідь: 57 м

3.2. Задачі з недостатніми значеннями даних величин або і взагалі з відсутніми певними даними, що дає змогу учням вчитися виконувати певні вимірювання, знаходити дані в таблицях і довідниках, які необхідні для розв’язування тих чи інших задач.

   При закріплені знань суттєве значення має самостійне вміння учнями знаходити та складати задачі з практичним змістом.

3.2.1. Мешканці чотирьох будинків вирішили викопати колодязь так, щоб відстань від нього до кожного будинку була однакова. Допоможіть знайти місце, де він має знаходитись, якщо будинки розташовані у вершинах : а)  прямокутника; б) рівнобічної трапеції; в) ромба.

Чи завжди дана задача має розв’язок?

Розв'язування

а) проводимо діагоналі прямокутника, точка перетину яких і є центром описаного навколо нього кола та рівновіддалена від

                                   його вершин.

б) проводимо два серединних перпендикуляри до сторін трапеції, точка перетину яких і є центром описаного навколо неї кола та рівновіддале-

                                на від її вершин.

в) задача не завжди матиме розв'язок, як бачимо на прикладі ромба. Потрібно, щоб суми протилежних кутів чотирикутника дорівнювали .

Дана задача представлена учнем у вигляді презентації з ефектом анімації.

3.2.2 Кількість еритроцитів ( з розрахунку на 1 мм³ ) в крові людини становить на рівні моря – 5 мільйонів. Яка кількість еритроцитів буде в крові людини, якщо вона підніметься на вершину гори 48000м?

Розв'язування. З медичного довідника знаходимо наступні відомості: через кожні 600 м підняття в гору кількість еритроцитів  збільшується на 1 мільйон. Задача на збільшення еритроцитів на однакову кількість – це задача на арифметичну прогресію. Встановимо скільки раз відбудеться це збільшення (разів).

 Отже:

Маємо:

(млн.)

Відповідь 13 млн. еритроцитів.

3.2.3 Скільки тон сталевих труб пішло на спорудження газопроводу завдовжки 4450 км, якщо його зовнішній діаметр 1420 мм, а товщина труби 22 мм?

 

Розв'язування. Складемо геометричну модель цієї задачі. Сформулюємо цю проблему інакше. Так як маса тіла залежить від об’єму та густини, то необхідно знайти об’єм тіла, яке обмежене двома циліндрами з радіусами основ 0,71 м і 0,688 м та висотою 4450000 м

     О₁            А₁   Дано: циліндр з радіусом

                                          R₁ = О₁А₁ = 0,71 м,

                                      циліндр з радіусом

                                          R₂ = OA = 0,688 м

      О         А      висота Н = О₁О = 4450000 м

                          Знайти: V тіла, обмеженого

                                        циліндрами

Розв’язування.

 

(м³)

З курсу фізики відомо, що , де густина сталі

Отже,

(т).

Відповідь: т

  Пропедевтика математичного моделювання в школі

4.1. Сутність метода математичного моделювання. За допомогою прикладних задач учні знайомляться із застосуванням математики у вирішенні окремих завдань, що ставить перед ними сучасне життя. Але використання цих задач під час навчання не дозволяє побачити технологію використання математичних фактів і методів при розв’язуванні практичних проблем.

  У законах України “Про загальну середню освіту”, Національній доктрині розвитку освіти, Державному стандарті базової і повної середньої освіти прописане головне завдання української освіти – підготовка компетентної особистості, що здатна знаходити правильні рішення у конкретних навчальних, життєвих і, в майбутньому, професійних ситуаціях. Математична компетентність - спроможність особистості бачити та застосовувати математику в реальному житті, розуміти зміст і метод математичного моделювання, будувати математичну модель, досліджувати її методами математики, інтерпретувати отримані результати, оцінювати похибку обчислень.

  Математичне моделювання настільки широко використовується для дослідження та вивчення навколишнього світу, що для оволодіння учнями кожного етапу повинно стати предметом постійної турботи учителя математики.

4.2.Створення першочергових уявлень. Підготовку учнів до математичного моделювання необхідно проводити у всіх класах, використовуючи різні форми і методи. Спочатку немає необхідності знайомити учнів з усіма етапами моделювання. Можна зорієнтувати їх на вміння виділяти суттєві фактори, знаходити правильні математичні шляхи, щоб вирішити дану проблему. Головне – закласти основу цих вмінь і довести до учнів розуміння того, що для розв’язку практичної задачі складається її математична модель, яка може мати форму текстової задачі, рівняння, нерівності або їх систем, функції та інше.

* Розглянемо задачу 1.2. Розв’язування. Кожний наступний крок учня в 2 рази менше за попередній, тому маємо спадну геометричну прогресію з . Знайдемо який шлях пройде учень, тобто суму довжин його кроків Для спадної геометричної прогресії маємо: (м). Зробимо висновок: максимально можлива відстань, яку за даних умов може пройти учень, дорівнює 2 метри. Тобто, учень не дійте до столу вчителя.

 Більше можливостей для пропедевтики математичного моделювання практичних задач з’являються при вивченні диференційного то інтегрального числення, розв’язку геометричних задач.

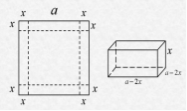  * Розглянемо задачу 1.3. Зробимо геометричну модель умови задачі.

Нехай ми в кутах картону відрізали квадратики зі стороною  х см. Тоді розміри коробочки становитимуть: а-2х, а-2х і х.

.

, (а – сторона).

Отримані критичні точки відмічаємо на прямій і встановлюємо знак похідної на отриманих проміжках.

   +    max             min      +

 

                                 

Відповідь: необхідно вирізати квадратики зі стороною В інших випадках об’єм не буде максимальним, що призводить до не економної витрати матеріалу.

   З досвіду роботи хотілось би зауважити, що доцільно використовувати задачі з шкільних підручників, бажано міжпредметного характеру, змінюючи в окремих випадках їх умови. Розглянемо наступні задачі.

4.2.1 При якому опорі реостата потужність електричного кола буде найбільшою?

Розв’язування

Сила струму

 ,

Потужність

                                           .

З іншої формули маємо - , де ε – електрорушійна сила, R – опір реостата,

r – внутрішній опір джерела. Тоді потужність будемо знаходити за наступною формулою .

Складемо функціональну залежність Позначимо R = x.   . Для знаходження максимального значення потужності знайдемо P′(x).

 

Знайдемо критичні точки.

         +        max     

 

                       r

Отже, потужність буде найбільшою при умові рівності опору  реостата і внутрішнього опору джерела, тобто R = r.

В даній задачі  математична модель була представлена у вигляді функціональної залежності. Учням слід пояснити, що якщо опори не будуть рівними, то потужність не буде максимальною, а це економічно не вигідно.

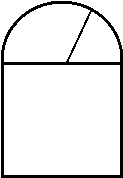
4.2.2 . Вікно має форму прямокутника, завершеного півкругом. Периметр вікна дорівнює а. При яких розмірах сторін прямокутника вікно буде пропускати найбільшу кількість світла?

Краща освітлюваність приміщення буде при великих розмірах вікон, тобто коли вони мають найбільшу, із можливих, площу поверхні. Побудуємо геометричну модель задачі.

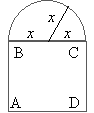Розв’язування

Нехай радіус півкола  дорівнює  х. Тоді сторона ВС = 2х. Виразимо сторону АВ через х і периметр а.

 .

Площа вікна складається з площі прямокутника і площі півкруга. Складаємо залежність S від x.    

 

   

             +  max

         

                  

BC= 2 x=, AB =  

Відповідь: вікно повинно мати форму квадрата зі стороною , тоді площа його буде найбільшою і освітлюваність, за ті самі витрачені кошти, найкращою.

4.2.3. На двох шахтах добувають руду. На першій – 100т в день, на другій – 200т в день. Цю руду є можливість обробляти на двох заводах, причому вартість перевезень (в умовних одиницях) однієї тони руди подано в таблиці.

	1 –й завод	2 –й завод
Перша шахта	5	4
Друга шахта	7	5

Відомо, що кожен завод може обробляти не  більше 250т. Руди. Скільки руди необхідно завозити з кожної шахти на кожний завод, щоб вартість перевезень була найменшою.

Розв’язування. Нехай х – кількість руди, яка перевозиться в день з 1–ї шахти на 1–й завод; у –кількість руди, яка перевозиться в день з 2 –ї шахти на 1 –й завод; тоді (100-х) –кількість руди, яка перевозиться в день з 1–ї шахти на 2–й завод; (200-у) –кількість руди, яка перевозиться в день з 2–ї шахти на 2-й завод. Використовуючи обмеження, отримаємо систему та її графічний розв’язок.

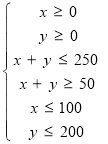
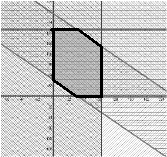
Витрати на перевезення:

5х+7у+4(100-х)+5(200-у)=х+2у+1400

Розв’язком задачі на максимум (мінімум) можуть бути координати однієї з вершин многокутника – розв’язку системи:

(50;0); (0;50); (0;200); (50;200); (100;100); (100;0). Підставляємо дані координати в цільову функцію х+2у+1400min

50+20+1400=1450; 0+250+1400=1500;

0+2200+1400=1850; 100+2100+1400=1700

100+20+1400=1500

Отже, найвигідніший план перевозок подано у вигляді таблиці

	1 –й  завод	2 –й  завод
Перша шахта	50т	50т
Друга шахта	0т	200т