Одночлен. Стандартний вигляд одночлена

Тема. Одночлен. Стандартний вигляд одночлена

Мета: домогтися свідомого розуміння змісту основних понять уроку (одночлен; одночлен стандартного вигляду, коефіцієнт одночлена стан­дартного вигляду; степінь одночлена); вдосконалювати вміння виконува­ти перетворення степенів.

Тип уроку: засвоєння знань учнів.

Хід уроку

I. Перевірка домашнього завдання

 Щоб перевірити корекцію самостійної роботи, збираємо зошити на перевірку та за необхідності висвітлюємо найскладніші завдання (з погляду учнів) попередньої самостійної роботи.

II. Робота з випереджальним домашнім завданням

Учні виконують завдання самостійно, використовуючи підручник та свої записи.

Після виконання завдання працюємо над корекцією.

III. Засвоєння нових знань

Отже, основними новими поняттями, які розглянуто у відповідному пункті підручника, є:

1) одночлен;

2) одночлен стандартного вигляду;

(Що таке «стандарт» — знайти в тлумачному словнику.)

3) коефіцієнт одночлена, записаного в стандартному вигляді;

(Що таке «коефіцієнт» — знайти в тлумачному словнику.)

4) степінь одночлена.

(Чи є тотожними поняття «степінь числа» та «степінь одночлена»?)

Зміст виділених понять учні знаходять самостійно й усвідомлюють, знайшовши числові порівняння.

IV. Закріплення знань. Формування вмінь, удосконалення навичок

Виконання усних вправ

1. Чи є одночленом вираз:

1) 3,4х²у;   2) -0,7ху²;      3) а ∙ (-8);    4) х² + х;   5) х²х;  6) - т³пт²;  7) а – b;

8) 2(х + у)²;   9) -0,3ху²; 10) с¹⁰;    11) -т;   12) 0,6?

 Вимагаємо від учнів пояснень, закріплюємо знання означення од­ночлена.

2. Чи записано у стандартному вигляді одночлен:

1) 6ху; 2) -2aba; 3) 0,5т ∙2n; 4) -bса; 5) - х³у³; 6) 5р³р² ?

 З метою виховання математичної культури звертаємо увагу на те, що в одночлені стандартного вигляду степені з різними основами записуємо в алфавітному порядку їх основ.

3. Назвіть коефіцієнт одночлена й визначте його степінь:

1) 3х⁵;  2) -7ху;  3) 6х² ∙ у;  4) 17;   5) -а⁵;  6) у.

Виконання письмових вправ

1. Зведіть одночлен до стандартного вигляду, вкажіть його коефіцієнт та
   степінь:

1) 8х³ ∙ хх⁵;  2) 3а ∙ 0,5b ∙ 4с;  3) 3а ∙ (-2ас);  4) -2т² ∙ 6mn³;

5) -2х³ ∙ 0,1х³у ∙ (-5у);   6) p ∙ (-q) ∙ p²⁰.

2. Складіть усі можливі одночлени стандартного вигляду з коефіцієнтом 5, що містять дві змінні х та у так, щоб степінь кожного одночлена дорівнював: 1) трьом; 2) чотирьом.
3. Знайдіть значення одночлена:

1) 4х², якщо х = -3;   2) -32а²b³, якщо а = , b = - 1;

3) х²у, якщо х = 7, у = 0,6;  4) 0,6аbс², а = 1,2, b = -5, с = 3.

4. Чому дорівнює об'єм прямокутного паралелепіпеда, ширина якого а
   см, довжина у 2 рази більша за ширину, а висота у 2 рази більша від довжини? Складіть і запишіть вираз до цієї задачі. Як ви назвете здобутий вираз? Обчисліть його значення при а =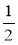 (м).
5. Обчисліть значення виразу: 1) 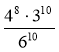; 2) .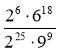

V. Підсумки уроку. Рефлексія

«Німий диктант»

На дошці записано одночлен стандартного вигляду та одночлен, що не є одночленом стандартного вигляду: 1) 7a³bc⁴; 2) 7а³bс ∙ с³.

Учитель почергово вказує на відповідні елементи запису, а учні повинні записати математичну назву загального поняття, що подається цим записом.

Наприклад:

• учитель указує на вираз 2) — учні записують «одночлен»;
• учитель вказує на вираз 1) — учні повинні записати «одночлен стандарт­ного вигляду» тощо.

VI. Домашнє завдання

№ 1. Зведіть одночлен до стандартного вигляду, вкажіть його коефіці­єнт та степінь: 

1)8у² ∙ у³ ∙ у; 2) 7 ∙ х ∙ 0,1у²z;  3) 5b ∙ (-3аb);   4) -2т⁴ ∙ 9тп³;

5) -3a² ∙ 0,2ab⁴ ∙ (-10b);    6) х³ ∙ (-у)³ ∙ х.

№ 2. Знайдіть значення одночлена:

1. 3х³, якщо х = -3; 2) 0,8т²пр, якщо m = -0,2, п = 3, р = 5.

№ 3. Випереджальне домашнє завдання. Знайдіть у підручнику при­клад на множення одночленів та піднесення одночлена до степеня. Про­читайте та знайдіть (виділить) знайомі та незнайомі поняття, властивості, алгоритми. Які саме властивості дій над числами є основою розв'язання прикладів (випишіть їх назву).