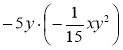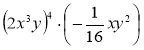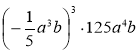Множення одночленів. Піднесення одночленів до степеня
Тема. Множення одночленів. Піднесення одночленів до степеня
Мета: вдосконалювати та розширювати спектр умінь виконувати перетворення добутку одночленів та степеня одночленів у одночлен стандартного вигляду; діагностувати засвоєні знання та вміння.
Тип уроку: застосування вмінь.
Хід уроку
І. Перевірка домашнього завдання
Із домашнього завдання найбільшу увагу привертають № 1 (4) та № 2 (6), бо містять степені з буквеними показниками. Тому саме ці приклади бажано ретельно перевірити (з паралельною корекцією записів у зошитах учнів). Усі інші приклади № 1 та № 2 перевірити можна так: учні заповнюють таблиці, використовуючи виконані вправи з домашнього завдання (під час виконання цієї роботи учні паралельно відновлюють у пам'яті поняття одночлена стандартного вигляду, його коефіцієнта та степеня). Таблиця для самостійного заповнення учнями має вигляд:
|
№ з/п |
Коефіцієнт |
Степінь |
Одночлен стандартного вигляду |
Корекція |
|
|
|
|
|
|
|
|
|
|
|
|
II. Актуалізація опорних знань
Виконання усних вправ
- Обчисліть значення виразу:
1) 23; 2) 5 ∙ 23; 3) 32; 4) 5 ∙ 23 – 32; 5) 62 – 3 ∙ 23; 6) (-1)3 – 10.
- Які з одночленів записано у стандартному вигляді? Назвіть для них коефіцієнт та степінь: 1) 2а4 ∙ 3b; 2) 0,5b4; 3) 3х2у2; 4) 4тп ∙ п.
- Яка з рівностей правильна? Чому?
1) 2a2b3 ∙ 3a4 = 6a2b7; 2) 2a2b3 ∙ 3а4 = 5a6b3;
3) 2a2b3 ∙ 3а4 = 6a8b3; 4) 2a2b3 ∙ 3a4 = 6a6b3.
III. Робота із випереджальним домашнім завданням
На дошці записано вирази:
1) 5a6 ∙ (-3 a2b)2; 2) 5a6 ∙ 9a4b2; 3) (-3a2b)2.
Оскільки учні вже повинні на цей час мати навички застосування алгоритму порівняння, то, напевно, на уроці швидко впораються із цією роботою і на запитання «Які висновки із порівняння ви могли б зробити?» повідомляють, що вираз 1) є добутком одночлена 5а6 на степінь одночлена (-3a2b), а тому, щоб спростити цей добуток, треба послідовно виконати такі дії: 1) піднесення одночлена -3а2b до 2-го степеня; 2) множення одночлена 5а6 на здобутий у п. 1) одночлен.
IV. Застосування вмінь
Вдосконаленню вмінь виконувати перетворення виразів, що містять степені, на цьому уроці сприяє розв'язування вправ достатнього рівня та застосування алгоритмів множення одночленів та піднесення одночлена до степеня.
Виконання письмових вправ
- Спростіть вираз:
а) 5а6(-3а2b)2; 2) (-х4у3)7 ∙ 8х2у5; 3) (-0,1а2bс5)2 ∙ (10bс2)3;
4)  ; 5)
; 5) 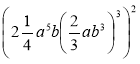 ;
;
6) 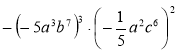 ; 7)
; 7) ![]() .
.
-
Подайте у вигляді добутку двох одночленів, один з яких дорівнює 4a2b3: 1) 8a3b5; 2) -20a10b3; 3) -4,8a2b7; 4) 2
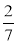 a15b6.
a15b6.
- Відомо, що 3аb4 = 5. Знайдіть значення виразу:
1) 1,2ab4; 2) 27a3b12; 3) -12a2b8.
№ 3 є дуже важливим щодо мотивації діяльності учнів, бо відповідає на запитання: «Під час розв'язування якої проблеми можуть бути застосовані вміння подавати одночлен у вигляді добутку одночленів або степеня деякого одночлена?»
V. Діагностика засвоєння
Як і раніше, пропонуємо самостійну роботу трьох рівнів складності.
|
І рівень |
|
|
Варіант 1 |
Варіант 2 |
|
1. Обчисліть значення одночлена: |
|
|
3х2у при х = -1; у = 2 |
5а2b при а = 2; b = -1 |
|
2. Зведіть одночлени до стандартного вигляду; вкажіть коефіцієнт та степінь: |
|
|
l) 3а2(-0,5a); 2) -аc7 ∙ 2c5а3 |
1) -2b ∙ 0,5b4; 2) -5a2b ∙ (-a4b3) |
|
3. Спростіть вираз: |
|
|
1) (3а2b)3; 2) -2а5 ∙ (-аb2)4 |
1) (5x2у)3; 2) 3b2(-а2b)3 |
|
4*. Замініть (*) так, щоб утворена рівність була правильною: |
|
|
1) 8a5b2 = -4ab∙(*); 2) (*)3 = |
1) 15х9у3 = -5х6у2 ∙ (*); 2) (*)2 = 0,49а2b8 |
|
II рівень |
|
|
Варіант 1 |
Варіант 2 |
|
1. Обчисліть значення одночлена: |
|
|
3х2у3 при х = -0,3; у = -2 |
2а3b2 при a = -2; b = - |
|
2. Зведіть одночлен до стандартного вигляду: |
|
|
1) |
1) |
|
3. Спростіть вираз: |
|
|
1) (-0,2аb4)4; 2)(-а3b7)2 ∙ 3аb7 |
1) (-0,5ху3)3; 2) 4х4у ∙ (-х2у4)2 |
|
4. Подайте вираз у вигляді: |
|
|
1) квадрата одночлена: |
|
|
|
|
|
2) куба одночлена: |
|
|
- 125х9у21 |
- 64а15b33 |
|
III рівень |
|
|
Варіант 1 |
Варіант 2 |
|
1. Обчисліть значення одночлена: |
|
|
-1000xy3 при х = - |
-270а3b при а = - |
|
2. Зведіть одночлен до стандартного вигляду: |
|
|
1) 2) -13а3bс ∙ (-0,1аb3с) ∙ 2с2 |
1) 2) 6х3у2 ∙ (-0,2xy2z2) ∙ (-0,5х3z) |
|
3. Спростіть вираз: |
|
|
1) 2) -(-а2b3)3 ∙ (-0,5а2b)2 |
1) 2) -(-аb4)2 ∙ (-0,3a3b)3 |
|
4. Відомо, що 2т3b = 5. Обчисліть значення виразу: |
|
|
1) 4т6b2; 2) -0,2т3b |
1) 8m9b3; 2) -10т3b |
VI. Підсумки. Рефлексія
Перевіряємо відповіді до вправ самостійної роботи. Учні здійснюють самоперевірку, самостійно визначають ті завдання, над якими треба попрацювати вдома (ті, що викликали найбільше запитань під час виконання самостійної роботи).
VII. Домашнє завдання
№ 1. Індивідуальне завдання. Учні виконують ті вправи самостійної роботи, що були визначені на попередньому етапі уроку як такі, що потребують доопрацювання.
Якщо деякі учні впоралися із самостійною роботою на високому рівні, то можна їм запропонувати вправи:
№ 2. Додаткове завдання. Знайдіть значення виразу:
1) (-4ху2)2п ∙ (4х3у2)2п, якщо х = - ![]() ; у = 2; п = 80;
; у = 2; п = 80;
2) (5kаk+1bk+2)2 ∙(5аb)k, якщо а = 0,1; b = 2; k = 51.
№ 3. Випереджальне домашнє завдання. Користуючись підручником, випишіть основні поняття з теми «Степінь з натуральним показником. Одночлен».
Складіть таблицю-довідник з названої теми (до таблиці 1 можна додати довідникову інформацію з теми «Одночлени»).

про публікацію авторської розробки
Додати розробку