Окремі випадки ділення натуральних чисел

Вчитель: Заєць Марія Олександрівна

Урок математики у 5 класі

Тема: «Окремі випадки ділення натуральних чисел»

Мета: : удосконалити вміння ділити натуральні числа; використовувати властивості ділення натуральних чисел; формувати навички розв'язувати задачі прикладного характеру; сприяти формуванню пізнавального інтересу; формувати вміння правильно і чітко висловлювати влас­ні думки, формулювати математичні твердження; виховувати дисциплінованість, позитивне ставлення до знань.

Тип уроку: засвоєння нових знань і формування вмінь.

Обладнання та матеріали:  комп’ютер, мультимедійна презентація, картки, кружочки-смайлики.

Хід уроку

1. Організаційний момент.

На початку уроку вчитель роздає учням заготовки кругів. Дітям необхідно на одній зі сторін намалювати смайлик, який характеризує їхній емоційний стан на початку уроку.

2. Перевірка домашнього завдання.

Вчитель збирає зошити на перевірку.

3. Актуалізація опорних знань.

Усне опитування:

1.               Що показує дія ділення?
2.               Назвати компоненти при діленні?
3.               Чи можна ділити на нуль?
4.               Що отримаємо якщо число поділимо на самого себе?

Математичні приклади (обчислити усно):

1). 25000 : 1

2). 180 : 180

3). 880 : 88

4). 0 : 12345

5). 360 : 60

6).   234 : 0

4. Повідомлення теми та мети уроку. Мотивація навчальної діяльності учнів.

Сьогодні ми з вами на уроці розглянемо та повторимо ділення натуральних чисел. Вивчимо правила за якими виконується ділення натуральних чисел. Розглянемо та вивчимо окремі випадки ділення, правила ділення на розрядну одиницю.

5.                  Вивчення нового матеріалу. Формування вмінь.

План

1). Ділення натуральних чисел.

2). Правила ділення натуральних чисел.

3). Ділення натурального числа на розрядну одиницю.

4). Окремі випадки ділення:

    а). ділення числа на самого себе;

    б). ділення на 1;

    в). ділення на 4;

    г). множення на 5 через ділення;

    д). множення на 25 через ділення.

Арифметична дія ділення

Дію, за допомогою якої за добутком та одним з множників знаходять інший множник, називають діленням.

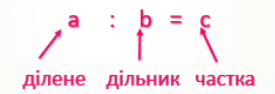
Якщо b > 1, то частка a : b означає, що число a зменшили в b разів.

Правильність виконання ділення можна перевірити множенням. Справді, 45 : 5 = 9, оскільки 5 ⋅ 9 = 45. Тому дія ділення є оберненою до дії множення.

Ділення натурального числа на розрядну одиницю

Щоб поділити натуральне число, що закінчується нулями, на розрядну одиницю, треба відкинути справа в цьому числі стільки нулів, скільки їх в розрядній одиниці.

Наприклад,

270 : 10 = 27;  3800 : 100 = 38;  123 000 : 1000 = 123.

Якщо ділене і дільник – це круглі числа (тобто ті, що закінчуються нулями), то слід знайти частку чисел, не звертаючи увагу на нулі, а потім забрати стільки нулів, скільки їх є у дільнику. Наприклад: 125 000 : 50 = 2 500;  360 : 60 = 6; 125 : 5 = 25 .

На замітку:

Якщо один із множників ділиться на деяке число, то і добуток цих множників ділиться на це число.

Якщо добуток двох чисел потрібно поділити на деяке число, то можна один із множників поділити на це число і одержаний результат помножити на другий множник.

Наприклад, (25 ∙ 12) : 5 = (25 : 5) ∙ 12 = 60.

Окремі випадки ділення

а : а = 1         а : 1 = а          0 : а = 0

На нуль ділити не можна!

Припустимо, що 8 : 0 дорівнює деякому числу b. Тоді b ⋅ 0 = 8. Але ця рівність неправильна. Якщо припустити, що c – певне число і 0 : 0 = c, то отримаємо, що c ⋅ 0 = 0, але ця рівність правильна для безлічі різних значень c. Отже, ділення на нуль не має смислу.

Щоб поділити число на 4, можна це число двічі поділити навпіл.

Наприклад, 404 : 4 = 404 : 2 : 2 = 202 : 2 = 101.

Щоб помножити число на 5, можна це число поділити на 2 і помножити на 10. Або спочатку помножити на 10, а потім поділити на 2.

Наприклад, 16 ⋅ 5 = 16 : 2 ⋅ 10 = 8 ⋅ 10 = 80;

25 ⋅ 5 = 25 ⋅ 10 : 2 = 250 : 2 = 125.

Щоб помножити число на 25, можна це число поділити на 4 і помножити на 100. Або спочатку помножити на 100, а потім поділити на 4.

Наприклад, 16 ⋅ 25 = 16 : 4 ⋅ 100 = 4 ⋅ 100 = 400;

18 ⋅ 25 = 18 ⋅ 100 : 4 = 1800 : 2 : 2 = 900 : 2 = 450.

6.        Фізкультхвилинка.

Робота з підручником.

Виконання задач і вправ 2-4 рівня складності

( № 390 - усно, 394, 396, 408, 415 - письмово).

7.        Закріплення знань. Формування вмінь.

1.         Завдання.

2.         Завдання.

Зі складу двома автівками вивезли 3500 кг цукру. На одну автівку навантажили 32, а на другу — 38 мішків. Скільки кілограмів цукру навантажили на кожну автівку, якщо кількість цукру в кожному мішку була однакова?

3.         Завдання (індивідуальне).

Виконати приклади на карточках.

Творче завдання (завдання на логіку).

На складі є ящики із цвяхами по 16 кг, 17 кг і 30 кг. Чи може комірник видати 113 кг цвяхів, не відкриваючи ящиків?

8. Підсумок уроку.

Продовжіть речення:

-         На уроці я дізнався про…

-         Сьогодні я навчився…

-         Найбільше мені сподобалося…

-         Я не зрозумів…

9.        Рефлексія.

На кружочках, отриманих на початку уроку, з іншої сторони дітям необхідно намалювати смайлик, який характеризує їхній емоційний стан на кінець уроку.

10.        Домашнє завдання.

1). Опрацювати параграф 9 ст. 57 – 60.

2). Вивчити правила.

3). Виконати вправи № 395, № 397, 418*.