Опис досвіду на тему "Різнорівневий підхід до навчання математики засобами інтерактивних технологій"
Запрошую колег ознайомитися з теоретико-практичним досвідом роботи за технологією різнорівневого навчання, пригадати, проаналізувати та за потреби застосувати у своїй педагогічній діяльності підходи до планування і проведення уроків, до контролю та оцінювання навчальних досягнень у системі інтерактивного навчання.
Скадовська спеціалізована загальноосвітня школа І-ІІІ ступенів «Академія творчості»
Різнорівневий підхід до навчання
математики засобами інтерактивних
технологій
Опис досвіду вчителя математики
спеціаліста вищої категорії
старшого вчителя
Гавриш Світлани Петрівни

Запрошую колег ознайомитися з теоретико-практичним досвідом роботи за технологією різнорівневого навчання, пригадати, проаналізувати та за потреби застосувати у своїй педагогічній діяльності підходи до планування і проведення уроків, до контролю та оцінювання навчальних досягнень у системі інтерактивного навчання.
Різнорівневий підхід до навчання на уроках математики - це один із способів оптимізації навчального процесу, основа розвивального навчання і тому вивчення та впровадження різнорівневого підходу виявляється необхідним для успішного навчання та виховання на сучасному етапі розвитку освіти.
Прискорення темпу життя, великий потік знань, що впливає на сучасну людину, потребує від неї вміння швидко знаходити необхідне рішення, використовуючи для цього пошукові методи, користуючись великою кількістю різноманітних джерел інформації. У зв’язку з цим, серед традиційних форм та методик навчання, у педагогічній практиці все частіше використовуються інтерактивні методи. Інтерактивні методи навчання досить швидко були визнані дієвим засобом впровадження нових освітніх технологій. Використання їх у практиці загальної середньої освіти повинно бути не фрагментарним, епізодичним, а системним, внаслідок розроблених відповідних технологій та готовності вчителів користуватися інформаційними технологіями та комп’ютерною технікою.
Метою такої технології є забезпечення освітнього мінімума для кожного учня та одночасне надання змоги кожному отримати освіту самого високого рівня у відповідності зі своїми можливостями і бажаннями.
Виходячи з мети, визначено такі завдання:
1.Проаналізувати теорію і практику впровадження інтерактивних освітніх технологій в диференційований навчальний процес та виявити зв’язок цього впровадження з тенденціями розвитку сучасного суспільства.
2. З’ясувати сутність інтерактивних освітніх технологій навчання та виокремити відповідні інноваційні аспекти діяльності у зв’язку з впровадженням цих технологій в навчальний процес.
3. Обґрунтувати і розробити методику впровадження інтерактивних технологій для реалізації різнорівневого навчання та дослідити вплив її використання на підвищення якості навчального процесу.
Методологічну основу досвіду становлять: технологічний підхід до розробки моделі впровадження інтерактивних освітніх технологій в навчальний процес з використанням комп’ютерної техніки; діяльнісний, особистісно-орієнтований, інформаційно-психологічний, синергетичний підходи до організації навчального процесу в загальноосвітньому навчальному закладі; Закони України „Про освіту”, „Про загальну середню освіту”, Національна доктрина розвитку освіти в Україні.
Для досягнення поставленої мети використано такі методи педагогічного дослідження: емпіричні спостереження, аналіз документації, інформативних комп’ютерних технологій та електронних документів, що розташовані у глобальній мережі Інтернет, вивчення педагогічного досвіду для визначення сучасного стану використання інтерактивних освітніх технологій в навчальному процесі; теоретичні методи використовувалися для аналізу, зіставлення та узагальнення літературних джерел щодо теми дослідження.
Практичне значення досвіду полягає в розробці та впровадженні отриманих результатів в організацію процесу навчання з використанням інтерактивних освітніх технологій.

В умовах класно-урочної системи навчання рівнева диференціація постає ефективним засобом формування в учнів самооцінки та самоконтролю.
До основних принципів рівневої диференціації можна віднести такі:
- виділення і відкрите пред’явлення учням результатів навчальних досягнень (за рівнями);
- “ножиць” між рівнями вимог навчання: рівень вимог має бути вищим за рівень навчальних
досягнень;
- формування опори: в усіх учнів класу незалежно від їхніх здібностей і навчальних можливостей повинні бути сформовані опорні знання та вміння;
- послідовності у просуванні за рівнями навчання;
- індивідуалізації, який дає змогу враховувати індивідуальний темп просування в навчанні;
- відповідності між змістом, контролем та оцінкою;
- добровільності у виборі рівня навчання: кожен учень добровільно вибирає рівень засвоєння навчального матеріалу.
Застосування різнорівневого підходу дає змогу кожному учню працювати на будь-якому рівні навчальних досягнень і здобути відповідні результати.
Учень має не тільки обов’язки (зокрема, засвоїти матеріал на відповідному рівні), а й право, найважливішим із яких є право вибору – отримати відповідно до своїх здібностей і нахилів підвищену підготовку з предмета чи обмежитись середнім або достатнім рівнями засвоєння матеріалу.
Отже, вчитель організовує навчання на всіх чотирьох рівнях навчальних досягнень (початковий, середній, достатній та високий), а учень сам вибирає рівень засвоєння навчального матеріалу.
Серед позитивних результатів різнорівневого підходу слід назвати такі:
- зменшення навантаження на дітей, які інколи не тільки з соціальних, а й з фізіологічних причин не можуть опанувати високий рівень навчальних досягнень;
- отримання кожним учнем потрібного саме йому змісту навчання математики;
- зникнення страху учня перед оцінюванням;
Різнорівнева технологія навчання передбачає:
- збільшення кількості вправ, які потрібно виконати, та забезпечення розвивального характеру навчання;
- відмову від авторитарного навчання;
- свободу вибору кожним учнем рівня навчальних досягнень;
- використання різних форм роботи.
Для успішного проведення різнорівневого навчання вчителю необхідно:
- вивчити індивідуальні особливості та навчальні можливості учнів;
- визначити критерії об’єднання учнів у групи;
- використовувати й удосконалювати здібності і навички учнів у груповій та індивідуальній роботі;
- систематично й об’єктивно аналізувати роботу учнів;
- планувати діяльність учнів з формування в них навичок самостійної діяльності і вміння керувати власним навчальним процесом;
- відмовлятися від малоефективних прийомів організації навчання, заміняючи їх раціональнішими за даних умов;
- здійснювати постійний зворотний зв’язок на уроці;
- вміло використовувати засоби заохочення тощо.
Ефективною формою реалізації рівневої технології є об’єднання дітей у групи з урахуванням їх самооцінки. У кожній групі слід пропонувати учням добірку завдань на вибір. Тоді кожний учень має просуватися від зони найближчого розвитку до зони актуального розвитку. Така організація роботи можлива, якщо вчитель знає мотивацію навчання кожного учня, а також рівень засвоєння кожним попереднього матеріалу. Оскільки в диференційованих завданнях прискорюється період від дій у співпраці з учителем до частково або повністю самостійної роботи, то слід цілеспрямовано формувати в учнів уміння і навички працювати самостійно.
Диференціація може здійснюватися за обсягом або змістом матеріалу, мірою допомоги вчителя та іншими ознаками. Групи учнів не постійні, їх кількісний і якісний склад може змінюватися залежно від рівня досягнень учнів, змісту теми тощо. Об’єднуючи учнів у групи, вчитель одержує можливість організувати навчання різне за змістом, рівнем складності, обсягом завдань, тобто враховує індивідуальні запити школярів за певних умов.
У процесі використання різнорівневих завдань необхідно здійснювати поступовий перехід від колективних форм роботи учнів до частково самостійних і повністю самостійних у межах уроку або системи уроків. Такий підхід дає можливість учням брати участь у виконанні завдань, складність яких зростає.
Узагальнення власних напрацювань і досвіду інших дає змогу виділити сукупність педагогічних вимог до роботи вчителя, за яких навчання на різних рівнях стає ефективним. Учителю необхідно:
- враховувати загальну готовність учнів до наступної діяльності;
- передбачати труднощі, які можуть виникнути в учнів під час засвоєння матеріалу;
- використовувати диференційовані завдання індивідуального та групового характеру в системі уроків;
- проводити перспективний аналіз діяльності власної та учнів: з якою метою планується виконання тих чи інших завдань, чому їх треба виконувати саме на даному етапі уроку, як продовжити розпочату роботу на наступних уроках.
На сучасному етапі реформування освіти в цілому та середньої школи зокрема, в умовах переходу на новий зміст і структуру навчання актуальною формою диференціації стала профілізація освіти. Саме диференціація дає змогу за рахунок змін у структурі, змісті та організації освіти враховувати інтереси, схильності та здібності учнів. Профілізація сучасної освіти орієнтується на широку диференціацію, варіативність, багатопрофільність та інтеграцію загальної і допрофесійної освіти.
Профільне навчання – це один із способів досягнення всіма дітьми загальноосвітньої мети у навчанні з урахуванням їх індивідуальних особливостей.
Профільна диференціація навчання математики повинна:
- забезпечити необхідний загальнокультурний рівень математичної підготовки молоді, який визначається замовленням суспільства й можливостями учнів даного віку;
- задовольнити потреби профільної підготовки в розвитку пізнавальних і математичних видів діяльності учнів, що характерні для даного профілю;
- формувати засобами математики професійні нахили учнів.
Профільна диференціація навчання математики передбачає:
- створення умов для свідомого вибору учнями профілю;
- наступність з допрофільним навчанням математики і навчанням математики у звичайних класах загальноосвітньої школи;
- досягнення всіма учнями базового рівня навчання математики;
- розробку державних стандартів з математики для різних профілів навчання;
- реалізацію прикладної спрямованості навчання математики, орієнтованої на профіль навчання як одного з головних засобів формування профільних інтересів засобами математики;
- відмінність змісту навчання математики в профільних класах і звичайних класах;
- реалізацію рівневої технології, що підсилює диференціацію навчання математики для кожного профілю;
- різномаїтість форм і видів класної та позакласної роботи;
- поглиблене вивчення математики, як одного з видів профільного навчання.
Для здійснення різнорівневого навчання в умовах профілізації намітились кілька основних тенденцій. Пріоритетним є організація такої діяльності вчителя, яка спрямована на набуття старшокласниками навичок самостійної науково-практичної, дослідницько-пошукової діяльності, на розвиток інтелектуальних, творчих якостей учнів та їх прагнення до саморозвитку і самоосвіти.

Саме різнорівневе навчання реалізує дві діалектично протилежні тенденції розвитку сучасної освіти: інтеграцію, яка обумовлена об’єктивними процесами взаємозв’язку і взаємозалежності різних наукових дисциплін, та спеціалізацію, яка відповідає різноманітності задатків і здібностей учня, його індивідуальним нахилам до того чи іншого виду діяльності.
Різнорівневе навчання в умовах профілізації передбачає врахування освітніх потреб, нахилів, здібностей учнів; забезпечення можливостей для рівного доступу учнівської молоді до здобуття загальноосвітньої профільної та початкової допрофесійної підготовки, неперервної освіти впродовж усього життя, виховання особистості, здатної до самореалізації, професійного зростання й мобільності в умовах реформування сучасного суспільства.
Однією із складових успіху засвоєння знань учнями на відповідному їм рівні та допомоги вчителю при організації роботи на уроці є різнорівневі завдання. Великий внесок в розробку і використання різнорівневих завдань зроблений Капіносовим А.М. На його думку, вчитель має розуміти, що за диференціацією учнів стоїть також складання для них певних завдань, які будуть для них оптимальними не лише по рівню розвитку та успішності, а й з урахуванням їх здібностей, нахилів. Подана нижче схема є опорною для складання різнорівневих завдань. (рис. 1).
У процесі використання різнорівневих завдань необхідно здійснювати поступовий перехід від колективних форм роботи учнів до частково самостійних і повністю самостійних у межах уроку або системи уроків. Такий підхід дає можливість учням брати участь у виконанні завдань, складність яких зростає.
|
Задача навчання |
Вимоги до умінь учнів |
Відповідність рівню засвоєння |
Зміст завдання |
|
Формування фактичних знань |
Уміти відтворювати терміни, поняття, означення |
Репродуктивний (пізнання) – формальні знання. Вид пам’яті - механічний |
1. Що називається 2. Що таке 3. Дайте означення |
|
Формування фактичних знань (поняття, факти) |
Уміти відтворювати, пояснювати, підтверджувати прикладами |
Репродуктивний (розуміння) – елементарні знання. Вид пам’яті - механічний |
1.Скласти методом простої підстановки 2. Знайти в тексті 3. Пояснити 4. Завдання на використання елементарних знань для пояснення типових (стандартних) прикладів, явищ |
|
Формування уміння застосовувати знання на практиці |
Уміти відтворювати знання, пізнавати їх в новій ситуації |
Конструктивний (елементарні уміння). Вид пам’яті - логічний |
Завдання на використання знань за взірцем, пред’явлене учню в нестандартній ситуації (перед використанням знань їх потрібно перетворити) |
|
Формування уміння творчо використовувати наявні знання |
Уміти здійснювати перенесення знань в нову ситуацію |
Творче (перенесення) – вище уміння. Утворення нових психічних структур |
Творчі завдання |
Система різнорівневих навчальних завдань повинна:
- забезпечити різний темп просування в засвоєнні знань, умінь і навичок різними за рівнями розумового розвитку на даному етапі навчання учнями, забезпечувати при цьому засвоєння, застосування, а також необхідне закріплення понять, що вивчаються;
- будуватися за принципом поступового зростання складності, забезпечувати спочатку рівень обов’язкової підготовки, як основу диференціації навчання;
- сприяти загальному розвитку учнів;
- відповідати конкретним дидактичним цілям уроку, етапу навчання і узгоджуватися з формами навчальної діяльності;
- будуватися на базі діючих підручників із застосуванням додаткового дидактичного матеріалу;
- мати завдання трьох рівнів, які відповідали б розробленим в психології та методиці навчання математики рекомендаціям відповідно складності і ступеня проблемності, а також відомим в дидактиці рівням засвоєння знань і способів дій.
Засвоєння дидактичних знань та умінь забезпечується відповідним характером навчально-пізнавальної діяльності учнів. Рівень засвоєння складає результативну сторону рівня їхньої пізнавальної діяльності. Основним продуктом засвоєння учнями матеріалу в процесі диференційованого навчання мають стати різнорівневі знання та уміння. Кожний визначений нами рівень засвоєння навчального матеріалу характеризується якістю засвоєння.
Спроба диференціювати навчальний матерiал за рiзними рiвнями дає можливiсть перенести центр ваги у навчаннi на можливостi i прагнення самих учнів, зробити їх бiльш самостiйними у виборi об'єму змiсту навчального матерiалу та рiвня творчостi.
Сьогодні перед школою стоїть завдання не просто дати учням певні знання і вміння, а й сформувати таку людину, яка здатна творчо мислити, приймати рішення й адаптуватися в будь-яких умовах.
А виконанню цього завдання сприяють рівнева диференціація та індивідуальний підхід до кожного учня.
Пропоную фрагмент уроку формування умінь і навичок в 10 класі на тему „Степінь з раціональним показником" з урахуванням рівневої диференціації.
Протягом п'яти хвилин уроку фронтально повторюються теоретичні факти, необхідні для подальшого розвитку поняття степеня. Після цього учням пропонується наступна система вправ:
-
Обчислити:
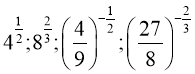
- Записати у вигляді степеня з дробовим показником:
![]()
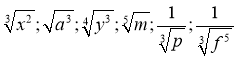
3. Записати у вигляді кореня:
![]()
4. Виконати дії:
![]() У наборі вправ передбачений і обов'язковий рівень з тим, щоб на його основі в подальшому здійснювати диференціацію. На виконання завдання відводиться 7 хвилин. За цей час учні виконують вправи і результати записують у зошити, після чого організовується їх самоперевірка. На зворотній стороні дошки або на екрані заздалегідь підготовлені відповіді. Вони порівнюються з отриманими. Як правило, є учні, які припустилися більше п'яти помилок. Оскільки за цю роботу учні не отримують фіксованих оцінок у журнал чи в зошит, у них немає підстав необ'єктивно показувати стан своїх знань і вмінь на цьому етапі уроку. Групу цих учнів назвемо першою групою. Для зручності надання допомоги їх можна посадити разом. Ті учні (друга група), які успішно впоралися з першим завданням продовжують працювати самостійно над виконанням наступної системи вправ на вибір.
У наборі вправ передбачений і обов'язковий рівень з тим, щоб на його основі в подальшому здійснювати диференціацію. На виконання завдання відводиться 7 хвилин. За цей час учні виконують вправи і результати записують у зошити, після чого організовується їх самоперевірка. На зворотній стороні дошки або на екрані заздалегідь підготовлені відповіді. Вони порівнюються з отриманими. Як правило, є учні, які припустилися більше п'яти помилок. Оскільки за цю роботу учні не отримують фіксованих оцінок у журнал чи в зошит, у них немає підстав необ'єктивно показувати стан своїх знань і вмінь на цьому етапі уроку. Групу цих учнів назвемо першою групою. Для зручності надання допомоги їх можна посадити разом. Ті учні (друга група), які успішно впоралися з першим завданням продовжують працювати самостійно над виконанням наступної системи вправ на вибір.
1. Скоротити дріб:
1)  2)
2) ![]() ; 3)
; 3) ![]()
4) 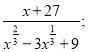 5)
5) 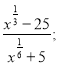 6)
6) 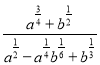 .
.
2. Спростити вираз: 1) 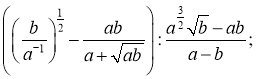
2) 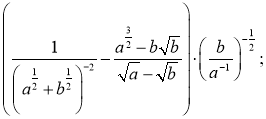
3) 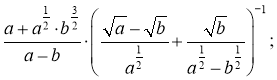
4) 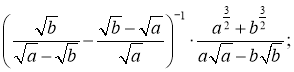
Для виконання цієї системи вправ характерним є перенесення знань у нову ситуацію.
Перші 4-5 хвилин учні другої групи працюють самостійно. Це дозволяє з першою групою учнів продовжити розв'язувати вправи обов'язкового рівня біля дошки в колективній формі.

Залежно від характеру помилок, учні аргументують дії з розв'язування завдань, спираючись на теоретичні факти. Так розглядаються вправи кожного із запропонованих завдань. Після колективної роботи цій групі учнів пропонується виконати аналогічну самостійну роботу. Вчитель перевіряє результати у кожного учня. Ті, що успішно справились із завданнями, приєднуються до другої групи учнів, а з рештою організовується індивідуальна робота. Якщо потрібно, проводяться консультації для другої групи. Досвід показує, що учні цієї вікової групи неохоче звертаються на уроці за допомогою до вчителя. Розуміючи нескладність запропонованих завдань, не бажають здатися безпорадними, і тому вважають за краще отримати її у однокласників.
На консультацію відводиться 2-3 хвилини. Учням про це відомо. Протягом цього часу кожен, хто зіткнувся з перепонами, може звернутися за допомогою до товариша. Знаючи рівень підготовки однокласників, кожен швидко знаходить необхідну допомогу. Під час консультації має виконуватись одна вимога: ніхто не продовжує письмову роботу далі. Одні учні пояснюють хід розв'язання, інші слухають, решта здійснює самоконтроль. Після того, як час вичерпано, учні займають свої місця і продовжують роботу самостійно. Якщо когось не задовольнить пояснення товаришів він може звернутися до вчителя. Трапляється так, що під час консультації для багатьох учнів одне й те саме запитання лишається без відповіді. У цьому випадку самостійна робота припиняється, і той, хто справився з завданням, пояснює розв'язання біля дошки. В кінці уроку відповіді, отримані учнями, порівнюються з правильними. Спершу багато учнів не встигають виконати запропоновані завдання, тому навіть оцінка „6" ставить їх у дискомфортний стан. У зв'язку з цим на уроці виставляються оцінки лише тим, хто отримав від 7 до 12 балів.
Одним із інструментів впливу на особистість учня у навчально-виховному процесі, регулятором, показником результативності, стимулом діяльності учня є оцінка. Василь Сухомлинський наголошував: «Оцінка — це найгостріший інструмент, використання якого потребує величезного вміння і культури» Форми і методи оцінювання навчальних досягнень учня можуть служити гуманізації навчального процесу, якщо вони сприяють розкриттю особистості, активізації його творчого та духовно-психічного потенціалу, але за певних умов і навпаки, можуть призводити до дегуманізації та відчуження особистості.
Досвід переконливо свідчить, що дитина, яка працює, потребує певного ставлення до того, що вона робить: схвалення, позитивної оцінки, засмучується негативній оцінці. Але якщо ця оцінка носить мотивований, індивідуально направлений характер і орієнтує учня в його власному розвитку, то вона має позитивні завдання і позитивні результати. Реалізує цю істину вчитель через активно-позитивний стиль стосунків зі своїми вихованцями. Даний стиль характеризується тим, що вчитель проявляє емоційно-позитивну направленість у відношенні до учня. Вона адекватно реалізується через їх поведінку, мовні висловлювання. Педагог дає найбільш високу оцінку позитивних якостей учнів і переконаний, що в кожного з них є певні достоїнства, які при відповідних зусиллях вчителя розкриваються і розвиваються. В індивідуальних характеристиках своїх учнів він відзначає позитивний ріст і якісні зміни. Якщо учень розв’язав задачу з помилкою, то не слід поспішати виставляти йому низький бал. Бажано дати йому час на знаходження власної помилки і якщо учнем помилку знайдено, то й бали знижувати не треба.
Результати своєї роботи на уроці учні відмічають у талоні самоконтролю:
|
Талон самоконтролю
Прізвище, ім’я ___________________ Клас ___________
|
Ефективним для вироблення у школярів умінь самооцінки можна вважати прийом складання учнями тексту контрольної роботи. Учням пропонується вдома підготувати і розв’язати такі завдання для тематичного оцінювання, які вони хотіли б отримати.
Щоб зацікавити школярів вивченням математики та досягти більш високих результатів навчання, використовується тестова перевірка вмінь і навичок учнів. Правильно організована і постійно діюча тестова перевірка мобілізує учнів, зацікавлює навіть слабо встигаючих, які не дозволяють собі бути пасивними на уроці, тому що їх знання та навички розв’язування задач із кожної вивченої теми буде перевірено й оцінено. Максимальна оцінка за виконання тестового завдання – 10 балів. Для підвищення оцінки до 12 балів учню дається додаткове завдання, розв’язування якого вимагає творчого підходу, сприяє розкриттю творчих здібностей дитини.
Нагальною потребою сучасної системи освіти при викладанні математики - є впровадження нових форм та методів навчання і виховання, що забезпечують розвиток особистості кожного школяра.
Розв'язанню цієї проблеми сприяє впровадження інтерактивних технологій навчання на уроках математики. Саме вони ефективніше, ніж інші педагогічні технології, сприяють інтелектуальному, соціальному й духовному розвитку школяра, готовність жити й працювати в гуманному, демократичному суспільстві.
В. Сухомлинський говорив, що школа має бути не коморою знань, а середовищем думки. Тоді предмет, що його викладає вчитель, стає не кінцевою метою його діяльності, а засобом розвитку дитини.
Під час інтерактивного навчання учні вчаться бути демократичними, спілкуватися з іншими людьми, критично мислити, приймати продумані рішення, виховувати почуття толерантності.
Суть інтерактивних технологій полягає в тому, що навчання відбувається шляхом взаємодії всіх, хто навчається. Це співнавчання (колективне, кооперативне навчання, навчання у співпраці), у якому вчитель і учні є суб'єктами. Учитель виступає лише в ролі організатора процесу навчання, лідера групи учнів. Iнтерактивні технології найбільше відповідають особистісно зорієнтованому підходу до навчання. У процесі застосування інтерактивних технологій, як правило, моделюються реальні життєві ситуації, пропонуються проблеми для спільного вирішення, застосовуються рольові ігри. Тому інтерактивні технології найбільше сприяють формуванню в учнів умінь і навичок, виробленню особистих цінностей, створюють атмосферу співробітництва, творчої взаємодії в навчанні. Інтерактивні технології дають можливість забезпечити глибину вивчення змісту. Учні освоюють усі рівні пізнання (знання, розуміння, застосування, аналіз, синтез, оцінку). При цьому відсоток учнів, які засвоїли знання, досить високий. Змінюється роль учнів. Вона активна: учні приймають важливі рішення щодо процесу навчання. Змінюється основне джерело мотивації навчання. Воно стає внутрішнім, це інтерес. Досвід показує, що серед інтерактивних технологій ефективною є технологія навчання математики з використанням «ключових задач».
Найефективнішою є така типізація уроків за способом діяльності:
1. Уроки-лекції передбачають подачу матеріалу укрупненими блоками і мають наступні структурні етапи:
• обґрунтування необхідності вивчення теми;
• постановка проблемних завдань і аналіз їх ситуацій;
• опрацювання основних теоретичних положень теми;
• обговорення системи запитань до теми, які органічно пов'язані зі змістом лекції і будуть винесені на самостійне опрацювання;
• повідомлення матеріалів до заліку;
• розбір розв'язування «ключових» задач.
2. Уроки розв'язування «ключових» задач.
Учитель виділяє у кожній темі 7-8 основних, базових задач, що використовуються як окремі елементи способів розв'язування інших задач; вчить учнів їх розпізнавати, розв'язувати і навіть складати. Розв'язування цих задач можна записувати в окремий зошит-довідник з прийомів розв'язування «ключових» задач, яким можна користуватись за будь-яких умов.
Алгоритм розв'язування таких задач відповідає програмним вимогам. Уміння використовувати їх у нестандартних ситуаціях, при розв'язанні задач підвищеного рівня вимагається тільки від учнів з пізнавальними інтересами до математики.
Можна виділити такі види робіт з «ключовими» задачами:
• розв'язування задачі різними способами;
• розв'язування системи задач;
• перевірка розв'язування задач іншими учнями;
• самостійне складання задач: аналогічних, обернених, узагальнених, на застосування.
• розв'язування конкурсних та олімпіадних завдань – участь у змаганнях.
3. Уроки-консультації проводяться у формі відповідей учителя на запитання учнів, які їх цікавлять або які не вдалося самостійно розв'язати.
Опрацювання нерозв'язаних задач на уроці-консультації ведеться за таким планом:
• задачі компонуються в групи за змістом, методом розв'язування, рівнем складності;
• із запропонованих задач виділяється одна або формулюється нова, розв'язування якої служить ключем до методики розв'язування задач всієї групи;
• формулюється і розв'язується одна задача, що подає типовий зразок опрацювання задач із різних груп;
• добираються ключові задачі до задач із груп;
• визначаються інформаційні джерела, що вміщують розв'язування окремих задач із різних груп;
• опрацьовується додаткова задача, важлива (на думку вчителя) для всіх.
 4. Залікові уроки.
4. Залікові уроки.
Організаційна структура заліку:
• учень виконує індивідуальне завдання за карткою;
• робота в парі: усний звіт керівнику, корекція учнем відповіді підшефного, діалог продовжується до повного розуміння суті завдання;
• оцінювання виконаної роботи: у залікову картку учень виставляє підлеглому три оцінки – за знання з теорії, за розв'язування задачі, за ведення зошита, причому якість розв'язування кожної задачі з картки характеризується умовною позначкою;
• оголошується мотивація кожної оцінки;
У своїй роботі можна керуватися такими правилами організації інтерактивної роботи учнів:
1. До роботи повинні бути залучені різною мірою всі учні.
2. Необхідно дбати про психологічну підготовку учнів. Корисними є: різноманітне та постійне стимулювання учнів за активну участь у роботі; надання можливості для самоорганізації та ін.
3. Тих, хто навчається в інтерактивні, не повинно бути багато. Продуктивна робота в малих групах. Кожен має бути почутий.
4. Приміщення має бути спеціально підготовленим. Учні повинні мати змогу легко пересуватися під час роботи в малих групах. Усі матеріали для роботи малих груп готуються заздалегідь.
5. Під час уроку необхідно дотримуватись регламенту та процедури, проявляючи терпимість до будь-якої точки зору. Уважно вислуховувати всіх учасників, поважаючи їх.
6. Уважно ставитися до учнів під час формування груп.
7. На одному уроці бажано застосовувати 1-2 інтерактивних прийоми роботи.
8. Під час підготовки питань учителю необхідно продумувати різні варіанти можливих відповідей і заздалегідь виробляти критерії прийняття узгодженого рішення.
Уроки мають захоплювати учнів, пробуджуючи в них інтерес і мотивацію, навчати самостійному мисленню та діям. Ефективність і сила впливу на емоції та свідомість учнів значною мірою залежать від умінь і стилю роботи вчителя.
Інтерактивні вправи на уроках математики орієнтовані на:
- розвиток належності мислення школярів, певної самостійності думок: спонукають учнів до висловлення своєї думки, стимулюють вироблення творчого ставлення до будь-яких висновків, правил тощо. Деякі з інтерактивних вправ (наприклад, "Робота в парах", "Робота в групах", "Карусель", "Пошук інформації" та інші) спрямовані на самостійне осмислення матеріалу, допомагають замислитися ("Чи справді це так?"), дослідити факти, проаналізувати алгоритм розв'язків, зрозуміти їхню суть, перевірити і себе і свого товариша, знайти помилку;
- розвиток опору до навіювання думок, зразків поведінки, вимог інших: спонукають учнів до відстоювання власної думки, створюють ситуацію дискусії, зіткнення думок. Застосування вправ "Аналіз ситуації", "Вирішення проблем", вчать дітей протистояти тиску більшості, відстоювати свою думку. Виявити помилку у судженнях, відповідях, вказати за неї і довести це спонукає завдання, де вчитель допускає помилки. Коли в завданнях наявна певна проблемна ситуація, то розв'язання їх в умовах інтерактивних технологій активно стимулює діяльність мислення, спрямовану на подолання протиріччя, непорозумінь. Інколи корисно вчителю сформулювати неправильне твердження та «довести» його, а учням запропонувати знайти помилку в міркуваннях.
Ось приклад такого твердження: для довільних чисел n і m має місце рівність m=n.
Розв’язання: Нехай m![]() n. Тоді маємо:
n. Тоді маємо:
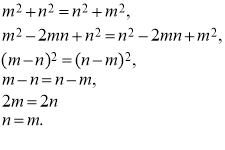
Помилка полягає в тому, що з рівності ![]() випливає не рівність
випливає не рівність ![]() а
а ![]() Можна запропонувати розв’язання, яке має принципові помилки, а учні їх повинні знайти. Наприклад, таке розв’язання:
Можна запропонувати розв’язання, яке має принципові помилки, а учні їх повинні знайти. Наприклад, таке розв’язання:
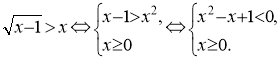 Отже, нерівність розв’язку не має.
Отже, нерівність розв’язку не має.
Як видно, відповідь правильна. Але вже при переході від нерівності до системи порушено рівносильність, бо нерівність даного типу може мати розв’язки і тоді, коли її права частина від’ємна. Тут, коли ![]() вираз у лівій частині невизначений. Аналогічний приклад:
вираз у лівій частині невизначений. Аналогічний приклад:
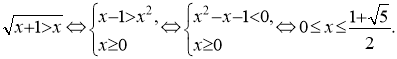 У цьому випадку така сама помилка приводить до неправильної відповіді.
У цьому випадку така сама помилка приводить до неправильної відповіді.

Інтерактивні методи та прийоми навчання є частиною особистісно-орієнтованого навчання, оскільки сприяють соціалізації особистості, усвідомлення себе як частини колективу, своєї ролі і потенціалу. Спираючись на власний досвід, до найефективніших з них належать:
1. Акваріум
Учасники об'єднуються у групи по 4–6 осіб та ознайомлюються із завданням. Одна з груп займає місце в центрі класу, отримує інструкцію щодо проведення групової дискусії: «Прочитайте завдання вголос, обговоріть його в групі, за 3–5 хвилин дійдіть спільного рішення або підсумуйте дискусію».
Наприклад, на уроці алгебри у 7 класі «Розв’язування систем лінійних рівнянь різними способами» була використана технологія «Акваріум» під час розв’язування задач у групах.
Завдання для груп.
І група
Приклад № 1. Розв'язати графічним способом систему рівнянь
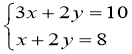
II група
Приклад № 2. Розв'язати систему рівнянь способом підстановки
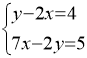
III група
Приклад № 3. Розв'язати систему рівнянь способом додавання
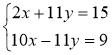
Після завершення відведеного часу група повертається на місце. Коротке обговорення того, що почули всім класом: чи погоджуєтеся ви з думкою групи? Чи була ця думка достатньо аргументованою? Потім інша група займає місце в центрі кола. Наступна група може обговорювати інше питання або іншу проблему.
2. Коло ідей
Метою прийому є залучення всіх до обговорення проблеми. Порядок проведення:
• учитель ставить дискусійне питання та пропонує обговорити його в групах;
• після того, як вичерпався час обговорення, кожна група представляє лише один аспект проблеми, що обговорювалася;
• групи висловлюються по черзі, поки не буде вичерпано всі варіанти відповідей;
• під час обговорення теми на дошці складається список зазначених ідей;
• узагальнюються висловлені думки, робляться підсумки.
3. Мозковий штурм
Метод розв'язування проблеми за обмежений час. Послідовність дій може бути такою.
Крок 1. Вступ. Формулювання проблеми. Постановка завдань, визначення терміну обдумування пропозицій.
Крок 2. Висловлення суджень, ідей. Реєстрація ідей на дошці.
Крок 3. Обґрунтування своєї ідеї тими, хто її висловив. Загальна дискусія навколо представлених ідей ( правильність, доцільність, оригінальність). Вибір найкращої ідеї.
Крок 4. Обґрунтування остаточного вибору. Підбиття підсумків уроку.
4. Мікрофон
Дає змогу кожному висловити свою думку з приводу чогось. Правила проведення такі: говорити має тільки той, у кого «символічний мікрофон», висловлені думки не оцінюються і не коментуються, під час виступу ніхто не має права перебивати, перепитувати.
Етап актуалізації опорних знань на уроці можна провести у формі фронтального опитування як інтерактивна вправа «Мікрофон». Наприклад, на уроці алгебри у 7 класі «Розв’язування систем лінійних рівнянь різними способами» учні висловлювали свою думку з таких питань:
1)Коли говорять, що дані рівняння утворюють систему?
2) Що називають розв’язком системи рівнянь з двома змінними?
3) Що означає розв’язати систему рівнянь з двома змінними?
4) У чому полягає зміст графічного способу розв’язування системи рівнянь?
5) Пояснити на прикладі зміст способу підстановки.
6) Як розв’язати систему рівнянь способом підстановки? і т. д.

5. Навчаючи – учусь
Прийом, що дозволяє передавати свої знання іншим. Учням роздаються аркуші з конкретною інформацією. Вони повинні ознайомитися з її змістом і передати одному з учнів класу, при цьому отримати також інформацію від іншого учня. Після спілкування учнів у парах представник від кожної групи повідомляє класу те, про що дізналися учні під час спілкування.
6. Ток-шоу
Застосовується для залучення учнів до діяльності з набуття вмінь публічно виступати. Планом передбачається:
1. Оголошення теми дискусії.
2. Пропозиція висловити думку окремим учням, які готувалися до дискусії із запропонованої теми.
3. Пропозиція глядачам поставити запитання до цих учнів(ті, які запитують і відповідають, повинні робити це в стислій, лаконічній формі).
7. Дискусія
Колективне обговорення спірного питання, обмін думками, ідеями між кількома учасниками. Правила ведення дискусії:
1. Сперечатися по суті.
2. Не допускати образливих реплік, не давати виступам оцінку. Не нав'язувати свою думку. Поважати погляди опонентів. Перш ніж критикувати, намагатися зрозуміти точку зору опонента.
3. Чітко формулювати свої думки, стримувати емоції.
4. Намагатися встановити істину, а не демонструвати красномовство.
5. Уміти усвідомити свою неправоту та дійти спільної думки.
8. Кооперативне взаємонавчання
Полягає в постійній взаємодії та взаємопідтримці учнів через взаємоперевірку самостійних робіт, спільне виконання домашніх завдань, переказ один одному вивченого матеріалу, спільну підготовку до заліку та ін.
9. Метод «американської мозаїки»
Реалізується за схемою: новий матеріал поділяється на 4–6 частин, які пропонуються для вивчення членам груп. Кожен учень із групи досконало опрацьовує одне питання з переліку. Потім члени різних команд, які вивчали одне й те саме питання, збираються для 5–10-хвилинного обговорення його. Після цього вони повертаються до своїх команд і пояснюють зміст своєї частини навчального матеріалу іншим членам групи. Рівень засвоєння навчального матеріалу визначається за результатами індивідуальної самостійної роботи, яку виконує кожний учень за всією темою.
10. Метод групового дослідження
Полягає в тому, що групи досліджують певне питання з теми підготовки доповіді або виступу. Питання розподіляються по групах так, щоб у результаті повідомлень був презентований увесь матеріал з нової теми. За підготовку доповіді вся група отримує оцінку.
Із прийомів контролю і самоконтролю найбільш ефективними є:
1. Взаємоопитування
Методик проведення взаємоопитування є декілька, але всі вони зводяться до того, що спочатку один учень слухає відповідь другого, потім ролі міняються. Запитання для опитування може пропонувати вчитель. Наприклад, на парти кладеться листок із десятьма запитаннями. Учні по черзі відповідають на них: один – на парні, другий – на непарні.
До видів взаємоопитування відносять також взаємоперевірку письмових відповідей, взаємоперевірку підсумкових контрольних робіт (проводиться за зразками правильних відповідей, які для слабких учнів дає вчитель).
2. Самоопитування. Учитель може провести його за декількома методиками.
• На дошці записуються запитання та пропонується учням дати відповіді на них «про себе». Учитель вивішує правильні відповіді, просить учнів порівняти власні відповіді з тими, що запропоновані як еталон. Порівнявши відповіді, учні самі собі виставляють оцінку.
• Учитель може самоопитування як таке не проводити взагалі, а просто попросити учнів підняти руку, хто вважає, що його підготовку до уроку можна оцінити на 10–12 балів; 7–9 балів; 1–3 бали.
• Учні дають відповіді на запитання, запропоновані вчителем, письмово. Потім проектуються правильні відповіді й учні на полях біля кожної своєї відповіді ставлять «+» або «–». Підрахувавши кількість плюсів, отримують оцінку. Виправлення помилок у зошиті не допускається.
3. Вибірковий контроль
Самостійну роботу виконує весь клас, але перевіряє вчитель тільки декілька робіт учнів.
4. Опитування ланцюжком
Учитель на дошці вивішує запитання. Учні по черзі відповідають на них.
5. Захисний лист
Перед опитуванням на стіл учителеві кладеться чистий аркуш паперу, на якому учні, не підготовлені до уроку, можуть вписати свої прізвища. Це дає підстави не опитувати цих учнів на уроці, але вчитель ураховує цю інформацію під час тематичного оцінювання.
6. 30 секунд на роздум
Під час фронтального опитування витримується пауза після кожного заданого запитання. Це дає змогу учням, які мислять повільно, підготуватися до відповіді.
7. Релейна контрольна робота
Проводиться за текстами раніше розв'язаних задач.
8. Світлофор
Усім учням роздаються картки двох кольорів: зелений – означає «Так», «Угору», «Праворуч»; червоний – «Ні», «Униз», «Ліворуч».
Після зачитування вчителем запитання учням дається певний час на обмірковування. Потім за командою всі піднімають картки, колір яких відповідає тим відповідям, які вважають правильними. Типи завдань:
1. Чи правильне твердження?
2. Чи правильно зроблений малюнок?
3. Чи правильно написана формула?
4. У якому напрямку відкласти координату точки?
Отже, для ефективного застосування інтерактивних технологій, зокрема щоб охопити весь необхідний обсяг матеріалу і глибоко його вивчити, треба старанно планувати свою роботу, щоб:
• дати завдання учням для попереднього підготування: прочитати, продумати, виконати самостійні підготовчі завдання;
• відібрати для уроку або заняття такі інтерактивні вправи, які дали б учням «ключ» до освоєння теми;
• під час самих інтерактивних вправ дати учням час подумати над завданням, щоб вони сприйняли його серйозно, а не механічно або «граючись» виконали його;
• на одному занятті можна використовувати одну (максимум – дві) інтерактивних вправ, а не їх калейдоскоп;
• дуже важливо провести спокійне глибоке обговорення за підсумками інтерактивної вправи, зокрема акцентуючи увагу й на іншому матеріалі теми, прямо не порушеному в інтерактивній вправі;
• проводити швидкі опитування, самостійні домашні роботи з різноманітних матеріалів теми, які не були пов'язані з інтерактивними завданнями.
Отже, застосування рівневої диференціації дає змогу кожному учню працювати на будь-якому рівні навчальних досягнень і здобути відповідні результати.
Різнорівневий підхід до навчання на уроках математики - це один із способів оптимізації навчального процесу, основа розвивального навчання і тому вивчення та впровадження різнорівневого підходу виявляється необхідним для успішного навчання та виховання на сучасному етапі розвитку суспільства та держави.

Уроки мають захоплювати учнів, пробуджуючи в них інтерес і мотивацію, навчати самостійному мисленню та діям. Ефективність і сила впливу на емоції та свідомість учнів значною мірою залежать від умінь і стилю роботи конкретного вчителя. Майстерність учителя допомагає дітям досягти найкращих результатів тими засобами, які найоптимальніші в кожній окремій ситуації


про публікацію авторської розробки
Додати розробку
