ОПОРНІ СХЕМИ " Вписані та описані кола"
Про матеріал
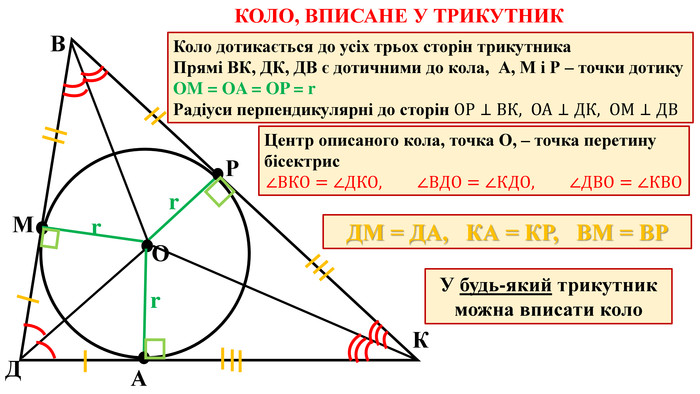
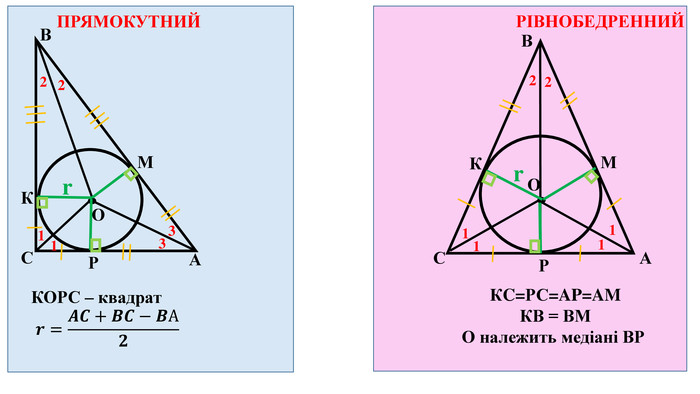
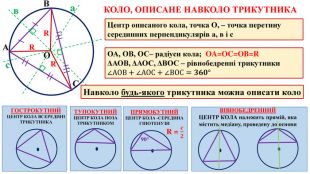
Узагальнені та систематизовані усі факти про описане коло навколо трикутника та вписане коло у трикутник, які повинні засвоїти семикласники.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



-

Ляшко Олена
26.10.2023 в 20:18
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Левадній Сергій Павлович
30.04.2023 в 17:45
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Самікова Ірина Олександрівна
04.02.2023 в 18:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Прохорчук Тетяна Павлівна
24.03.2021 в 19:13
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лучик Любов Василівна
14.05.2020 в 20:03
Дякую.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Степаненко Свелана
05.05.2020 в 19:03
Спасибо.Это то,что нужно мне.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 3 відгука