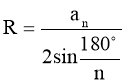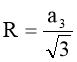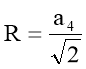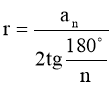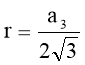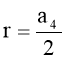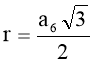Опорні конспекти 9 клас
Містять основні теоретичні питання курсів алгебри та геометрії, формули, зразки правильних записів,зауваження в стислому вигляді.

Види числових нерівностей

 Означення. Якщо а менше в або а більше в, то записують так: а<в або а>в.
Означення. Якщо а менше в або а більше в, то записують так: а<в або а>в.
Такий вираз називається нерівністю.( 7<10, 6,3>-10,2).
Теорема. Якщо різниця а-в—додатне число, то число а більше в, якщо різниця а-в—від’ємне число, то число а менше в.
(якщо а-в=7,02, то а>в; якщо а-в=-9,5, то а <в).

![]()
Знаки <, > називаються знаками строгих нерівностей.
Знаки≥, ≤ називаються знаками нестрогих нерівностей.
Властивості числових нерівностей
1. Якщо а>в, то в <а.
2. Якщо а>в та в>с, то а>с(властивість транзитивності).
3. Якщо а>в, то а+с>в+с.
4.Якщо а>в та с—додатне число(с>0), то ас>вс.
5. Якщо а>в та с—від’ємне число(с<0), то ас< вс.
6. Якщо а>в і с>d, тоа+с>в+ d.
7. Якщо а,в,с, d—додатні числа, причому а>в і с>d, то ас>вd.
8. Якщо а>в>0, то ![]() .
.
9. Якщо а>в>0, то для будь-якого натурального числа n виконується нерівність![]() .
.
|
Вид проміжку |
Геометричне зображення |
Позначення |
Запис за допомогою нерівностей |
|
Інтервал |
|
|
a<x<b |
|
Відрізок |
|
|
a≤x≤b |
|
Півінтервал |
|
|
a<x≤b |
|
Півінтервал |
|
|
a≤x<b |
|
Промінь |
|
|
x≥a |
|
Промінь |
|
|
x≤b |
|
Відкритий промінь |
|
|
x>a |
|
Відкритий промінь |
|
|
x<b |

 Лінійні нерівності.
Лінійні нерівності.
Означення. Лінійною називається нерівність виду ax>b(або, відповідно, ax<b, ax≥b, ax≤b), де а≠0 і в≠0.
Означення. Розв’язком нерівності з однією змінною називається множина таких значень змінної, яка перетворює її на правильну числову нерівність.
-
Якщо а >0, то розв'язок нерівності ax>b має вигляд
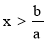

-
Якщо а <0, то розв'язок нерівності ax≥b має вигляд
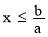
- Якщо а =0, то нерівність ax>b набуває вигляду ох>в, тобто вона не має розв’язку при в≥0 і правильна при будь-яких х, якщо в<0.
При розв’язуванні нерівностей використовуються такі властивості.
|
Властивості |
Приклади |
|
1. Якщо з однієї частини нерівності перенести в іншу доданок з протилежним знаком, то утвориться нерівність, рівносильна даній. |
4(у-1)+7≤1-3(у+2) 4у-4+7≤1-3у-6 4у+3у≤1-6+4-7 |
|
2. Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число, то утвориться нерівність, рівносильна даній. |
7у≤-8;
у≤-
|
|
3. Якщо обидві частини нерівності помножити або поділити на одне й те саме від’ємне число, змінивши при цьому знак нерівності на протилежний, то отримаємо рівносильну даній нерівность. |
-3х+8<2х-2 -3х-2х<-8-2 -5x<-10 x>2
|

Квадратична функція
Квадратична функція
Вираз 2х2-5х+3 є многочленом другого степеня з однією змінною.
Такі многочлени називаються квадратними тричленами.
|
Означення |
Приклади |
|
Коренем квадратного тричлена називається значення змінної, при якому значення цього тричлена дорівнює нулю. Для того, щоб знайти корені квадратного тричлена ах2+вх+с, треба розв’язати квадратне рівняння ах2+вх+с=0. |
Знайти корені тричлена 2х2-5х+3. Розв’яжемо рівняння 2х2-5х+3=0
D=25-24=1,
х1=1, х2=
Тобто, квадратний тричлен має розв’язки 1 та |
|
Якщо х1 і х2−корені квадратного тричлена ах2+вх+с, то ах2+вх+с=а(х- х1)(х- х2). |
2х2-5х+3=2(х-1)(х-
-2х2+5х+7=-2(х-
де х1= |
|
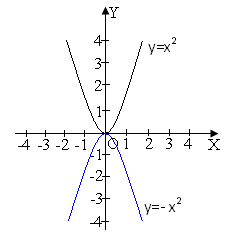
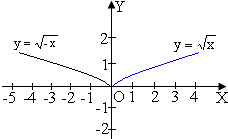
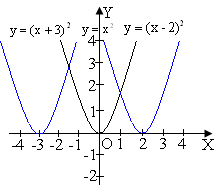
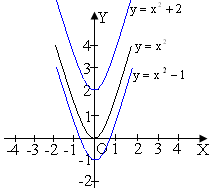
Квадратичною функцією називається функція, яку можна задати формулою виду у=ах2+вх+с, де х−незалежна змінна, а,в,с−деякі числа, причому а≠0. |
y=х2, у=- х2, у=х2+2,у=(х-4)2−приклади квадратичної функції. Їх графіки−параболи, тільки по-різному розташовані на на координарній площині. |
|
Графіки функцій у=ах2+вх+с і у=ах2−параболи, їх можна сумістити паралельним перенесенням, оскільки функцію у=ах2+вх+с можна представити у вигляді у=а(х+m)-n. |
Функцію у=2х2-4х+10 можна записати так у=2(х-1)2+8.
- |

Перетворення графіків функцій
|
№ |
Формула залежності |
Приклад |
Перетворення |
|
1 |
У=-f(x) |
|
Симетрія відносно осі Ох |
|
2 |
У=f(-x) |
|
Симетрія відносно осіОу |
|
3 |
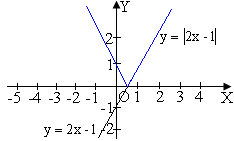
У=If(x)I |
|
Вище осі Ох−без змін, нижче осі Ох−симетрія відносно цієї осі |
|
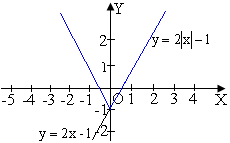
4 |
У=f(IxI) |
|
Правіше осі Оу−без змін і ця сама частина−симетрія відносно осі Оу |
|
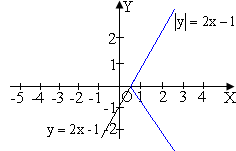
5 |
IУI=f(x) |
|
Вище осі Ох−без змін і ця сама частина−симетрія відносно Ох |
|
6 |
У=f(x-a) |
|
Паралельне перенесення вздовж осі Ох на а одиниць вправо, якщо а>0; на –а одиниць вліво, якщо а<0. |
|
7 |
У=f(x)+c |
|
Паралельне перенесення вздовж осі Оу на с одиниць вгору, якщо с>0, на –с одиниць вниз, якщо с<0. |
|
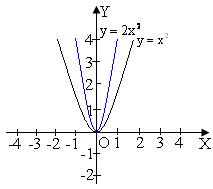
8 |
У=kf(x) (k>0) |
|
Таж сама форма, що і графік у=f(x), тільки розтягнутий вздовж осі Оу(від осі Ох) у к разів, якщо к>1 або стиснутий вздовж осі у (до осі Ох) |
|
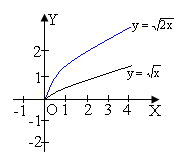
9 |
У=f(αx) (α>0) |
|
Таж сама форма, що і графік у=f(x), тільки стиснутий вздовж осі Ох(до осі Оу) у α разів, якщо α>1 або розтягнутий вздовж осі Ох(від осі Оу) у |
Розв’язування квадратних нерівностей
Означення Нерівність виду ах2+bх+с>0(ах2+bх+ с<0), де а, b, с−деякі числа а≠0 і х−змінна, називається квадратною.
Способи розв’язання:
1.Графічний.
−зображається схематичний графік функції у= ах2+bх+с з урахуванням напряму віток і нулів функції;
−розв’язком нерівності ах2+bх+с>0 є значення х, при яких точки параболи розташовані над віссю Ох;
− розв’язком нерівності ах2+bх+ с<0 є значення х, при яких точки параболи розташовані під віссю Ох;
−записуємо відповідь.
2. Метод інтервалів.
Якщо ліва частина нерівності є добутком лінійних множників, а права частина−0, тобто ƒ(х) >0(ƒ(х) <0) та ƒ(х)=(х-а)( х-b)( х-с)…( х-к), де а, b,с…к−деякі числа, то такі нерівності розв’язують методом інтервалів.
−знайти область визначення функції у= ƒ(х);
−нанести нулі функції (числа а, b,с…к) на числову вісь;
−поставити в крайньому правому проміжку, на які розбивається область визначення нулями функції, знак «+», а решта знаків чергуються.
(лінійні множники можуть знаходитись у степенях, якщо нуль функції «вийшов» із множника у парному степені, то при переході через нього знак не змінюється, а якщо в непарному степені−, то змінюється на протилежний);
 −записуємо відповідь.
−записуємо відповідь.
Числові послідовності
Арифметична прогресія
|
Означення |
Приклади |
|
Числова послідовність задана, якщо будь-якому натуральному числу n поставлене у відповідність деяке число аn. |
3; 10; 11; 13; 16; 20; … 4; 7; 10; 13; 16;… |
|
Послідовність задають за допомогою формули n-го члена , тоді неважко обчислити будь-який його член. |
Послідовність (аn)задана формулою аn=n3, nєΝ, 1; 8; 27; 64;… |
|
Послідовності бувають скінченні і нескінченні. Послідовність (аn) називається зростаючою (спадною), якщо для будь-якого номера n справедлива нерівність: аn+1 > аn (аn+1 <аn). |
2; 4; 6; 8; 10; 12;…−зростаюча.
|
|
Числова послідовність (аn), кожний член якої, починаючи з другого, дорівнює попередньому, до якого додане одне і те саме число, називається арифметичною прогресією. Це число позначають буквою d і називають різницею арифметичної прогресії. |
1; 3; 5; 7; 9−арифметична прогресія а1=1; d=2. 30; 25; 20; 15; 10; 5;… а1=30; d=-5.
|
|
Перші члени арифметичної прогресії будуть а1; а1+d; а1 +2d; а1+3d;… |
-50; -40; -30; -20;… а1=-50; d=10.
|
|
Формула n-го члена арифметичної прогресії аn= а1+d(n-1), nєΝ. |
а6=-50+10(6-1)=-50+10·5=0; а6=0. |
|
Характеристична властивість арифметичної прогресії: кожний її член, починаючи з другого, дорівнює середньому арифметичному сусідніх з ним членів, тобто Сума двох членів скінченної арифметичної прогресії, рівновіддалених від її кінців, дорівнює сумі крайніх членів. Формула суми перших n членів арифметичної прогресії:
|
4; 7; 10; 13; 16; … а1=4; d=3.
4+16=7+13
S5=
або S5=
|
Геометрична прогресія
|
Числова послідовність (bn), кожний член якої, починаючи з другого, дорівнює попередньому, помноженому на одне й те саме число, називається геометричною прогресією . Це число позначають q і називають знаменником геометричної прогресії. |
2; 4; 8; 16; 32; 64; … b1=2, q=2
1; |
|
Першими членами геометричної прогресії будуть: b1; b1q; b1q2; b1q3;… Формула n-го члена геометричної прогресії:
|
b1= |
|
Характеристична властивість геометричної прогресії: кожний її член, починаючи з другого, дорівнює середньому геометричному (середньому пропорційному) сусідніх з ним членів, тобто: bn2= bn-1· bn+1, n≥2, nєΝ. |
3; 9; 27; 81; 243;…
b32= b2· b4 тобто 272=9·81 |
|
Формула суми n перших членів геометричної прогресії:
nєΝ, q≠1. |
3; 9; 27; 81; 243;… b1=3 q=3
або |
|
Якщо (bn)−нескінченно спадна геометрична прогресія(ІqІ<1), то її сума обчислюється за формулою: |
|
Подібність фігур
Перетворення подібності
Перетворення фігури F у фігуру F' називається перетворенням подібності, якщо при цьому перетворенні відстані між точками змінюються в одне і те саме число разів. X'Y'=k· XY, k−коефіцієнт подібності.
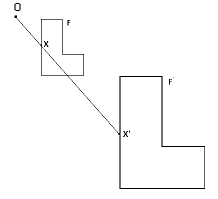 Нехай F−дана фігура і О−фіксована точка. Через довільну точку Х фігури F проведемо промінь ОХ і відкладемо на ньому відрізок ОХ', що дорівнює k·ОХ, де k−додатне число.Пертворення фігури F, при якому кожна її точка X переходить в точку X', побудовану таким способом, називається гомотетією відносно центра О. ОX'=k·ОХ, де k−коефіцієнт подібності.
Нехай F−дана фігура і О−фіксована точка. Через довільну точку Х фігури F проведемо промінь ОХ і відкладемо на ньому відрізок ОХ', що дорівнює k·ОХ, де k−додатне число.Пертворення фігури F, при якому кожна її точка X переходить в точку X', побудовану таким способом, називається гомотетією відносно центра О. ОX'=k·ОХ, де k−коефіцієнт подібності.
Властивості перетворення подібності
1.Перетворення подібності переводить прямі− у прямі, півпрямі− у півпрямі, відрізки− у відрізки.
2.Перетворення подібності зберігає кути між півпрямими.
Подібність трикутників
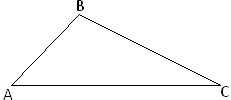
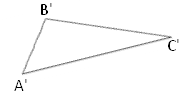 Два трикутники називаються подібними, якщо вони переводяться один в одного за допомогою перетворення подібності. Δ А В C ~ Δ А1 В1 C1.
Два трикутники називаються подібними, якщо вони переводяться один в одного за допомогою перетворення подібності. Δ А В C ~ Δ А1 В1 C1.
Властивості
1.У подібних трикутників відповідні кути рівні, а відповідні відрізки – пропорційні: ![]() А=
А=![]() А1;
А1;![]() В=
В=![]() В1;
В1;![]() С=
С=![]() С1;
С1;![]() 2.Відношення площ подібних трикутників дорівнює квадрату коефіцієнта подібності:
2.Відношення площ подібних трикутників дорівнює квадрату коефіцієнта подібності: 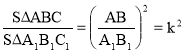 .
.
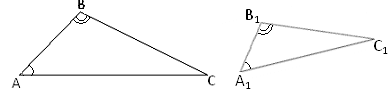
Ознаки подібності трикутників.
1.Якщо ![]() А=
А=![]() А1;
А1;![]() В=
В=![]() В1, то Δ А В C ~ Δ А1 В1 C1 – за двома кутами.
В1, то Δ А В C ~ Δ А1 В1 C1 – за двома кутами.
2.Якщо ![]() А=
А=![]() А1,
А1, ![]() , то Δ А В C ~ Δ А1 В1 C1 –за двома пропорційними сторонами і кутом між ними.
, то Δ А В C ~ Δ А1 В1 C1 –за двома пропорційними сторонами і кутом між ними.
3. Якщо ![]() , то Δ А В C ~ Δ А1 В1 C1 –за трьома пропорційними сторонами.
, то Δ А В C ~ Δ А1 В1 C1 –за трьома пропорційними сторонами.
Застосування подібності
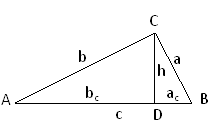 1.У трикутнику А В С
1.У трикутнику А В С ![]() С=90°, С D
С=90°, С D![]() А В . Висота прямокутного трикутника, проведена з вершини прямого кута, є середнім пропорційним (середнім геометричним) між проекціями катетів на гіпотенузу. h2=ac·bc.
А В . Висота прямокутного трикутника, проведена з вершини прямого кута, є середнім пропорційним (середнім геометричним) між проекціями катетів на гіпотенузу. h2=ac·bc.
 2.Катет прямокутного трикутника є середнім пропорційним (середнім геометричним) між проекцією цього катета на гіпотенузу і гіпотенузою. b2=bc·c a2=ac·c
2.Катет прямокутного трикутника є середнім пропорційним (середнім геометричним) між проекцією цього катета на гіпотенузу і гіпотенузою. b2=bc·c a2=ac·c
2.CD− бісектриса кута С. Бісектриса трикутника поділяє протилежну сторону на відрізки, пропорційні до прилеглих сторін. ![]() .
.
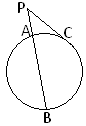
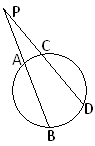 3.Якщо хорди АВ і СD перетинаються в точці S, тоАS·ВS=СS·DS.
3.Якщо хорди АВ і СD перетинаються в точці S, тоАS·ВS=СS·DS. 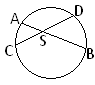
4. Якщо РА і РВ – січні до кола, то РА·РВ=РС·РD.
5. Якщо РА – січна, а РС – дотична до кола, тоРС2=РА·РВ.
Розв’язування трикутників
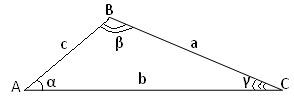 Теорема синусів
Теорема синусів
У довільному трикутнику сторони пропорційні до синусів протилежних кутів. Тобто ![]() .
.
Наслідки: 1. 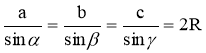 , де R− радіус описаного кола.
, де R− радіус описаного кола.
2.У трикутнику навпроти більшої сторони лежить більший кут,
навпроти більшого кута лежить більша сторона.
Теорема косинусів
У довільному трикутнику квадрат будь-якої його сторони дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними. Тобто с2=а2+b2-2·а·b·соsγ.
Наслідки:1.Якщо с2=а2+b2, то γ=90°, тобто трикутник прямокутний(теорема, обернена до теореми Піфагора).
2.Якщо с2<а2+b2, то кут γ−гострий; якщо с−найбільша сторона, то трикутник гострокутний.
 3.Якщо с2>а2+b2, то кут γ−тупий.
3.Якщо с2>а2+b2, то кут γ−тупий.
4. Сума квадратів діагоналей паралелограма дорівнює сумі квадратів всіх його сторін:
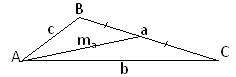 d12+d22 =2(а2+b2).
d12+d22 =2(а2+b2).
5. 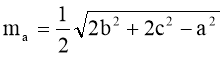 .
.
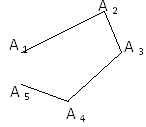 Многокутники
Многокутники
Ламаною А 1А 2…А nназивається фігура, яка складається з точок А 1, А 2, …А n та відрізків А 1А 2, А 2А 3, …, А n-1А n, які ці точки з’єднують. Точки А 1, А 2, …А n називаються вершинами ламаної, а відрізки А 1А 2, А 2А 3, …, А n-1А n – ланками ламаної. Ламана називається простою, якщо вона не має самоперетинів.Ламана називається замкненою, якщо її кінці співпадають.Довжиною ламаної називається сума довжин її ланок.
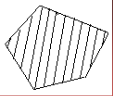
Опуклі многокутники
Проста замкнена ламана називається многокутником, якщо її сусідні ланки не лежать на одній прямій. Вершини ламаної називаються вершинами многокутника, а ланки ламаної− сторонами многогокутника. Відрізки, які з’єднують несусідні вершини многокутника, називаються діагоналями.Многокутник з n-вершинами, тобто з n-сторонами, називається n-кутником .
|
Простим многокутником або многокутною областю називається скінченна частина площини, обмежена многокутником. |
|
|
Многокутник називається опуклим, якщо він лежить в одній півплощині відносно будь-якої прямої, що містить його сторону. Кутом опуклого многокутника при даній вершині називається кут, утворений його сторонами при даній вершині. |
|
|
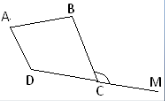
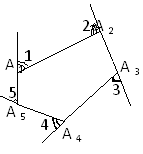
Зовнішнім кутом опуклого многокутника при даній вершині називається кут, суміжний із внутрішнім при даній вершині.
|
|
|
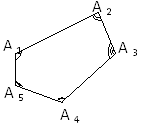
Сума кутів опуклого n-кутника дорівнює 180°·(n-2) |
|
|
Сума зовнішніх кутів опуклого n-кутника, взятих по одному при кожній вершині, дорівнює 360°. |
|
|
Многокутник називається вписаним в коло, якщо всі його вершини лежать на колі, яке, в свою чергу, називається описаним навколо многокутника. |
|
|
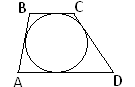
Многокутник називається описаним навколо кола, якщо всі його сторони дотикаються до кола, яке, в свою чергу, називається вписаним у многокутник. |
|
|
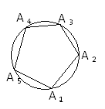
Опуклий многокутник називається правильним, якщо в нього всі сторони і всі кути рівні. |
|
|
Правильний опуклий многокутник є вписаним у коло і описаним навколо кола. Ці кола мають один і і той самий центр, який називається центром многокутника. |
|
|
Вершини правильного 2n-кутника, якщо їх брати через одну, є вершинами правильного n-кутника. |
|
|
У чотирикутника, описаного навколо кола, сума довжин протилежних сторін рівні і навпаки, якщо в опуклому чотирикутнику суми довжин протилежних сторін рівні,то в нього можна вписати коло. |
A B+CD=BC+AD |
|
У чотирикутника, вписаного в коло, суми протилежних кутів, дорівнюють 180° і навпаки.якщо в опуклого чотирикутника суми протилежних кутів дорівнюють 180°, то навколо нього можна описати коло. |
|
|
Якщо трапеція або ромб описані навколо кола,то їх висоти дорівнюють діаметру кола. |
|
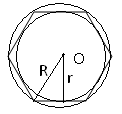
Формули радіусів вписаного і описаного кіл правильних многокутників
|
Кількість n |
n =3 |
n =4 |
n =6 |
|
|
|
|
|
|
|
|
|
|
Площі фігур
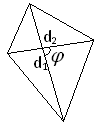 Довільний опуклий чотирикутник(d1, d2−діагоналі чотирикутника,
Довільний опуклий чотирикутник(d1, d2−діагоналі чотирикутника, ![]() −кут між діагоналями, S−площа):
−кут між діагоналями, S−площа):
S=![]() .
.
 Паралелограм : S=аhа=аb
Паралелограм : S=аhа=аb![]() =
=![]() .
.
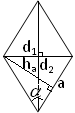
Ромб: S= аhа=а2![]() =
=![]() d 1d 2.
d 1d 2.
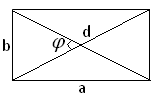
Прямокутник: S=аb=![]() .
.
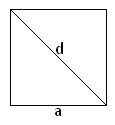
Квадрат: S=а2=![]() .
.
Трикутник(а, b, с−сторони; α, β, γ−протилежні їм кути, р−півпериметр, R−радіус описаного кола, r−радіус вписаного кола; hа , mа, lа−висота,медіана, бісектриса, які проведені до сторони а):
S=![]() аb
аb![]() ; S=
; S=![]() а hа; S=
а hа; S=![]() −формула Герона;
−формула Герона;
S= р r ; S=![]() .
.
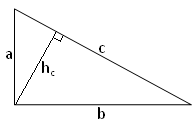 Прямокутний трикутник: S=
Прямокутний трикутник: S=![]() аb=
аb=![]() сhс.
сhс.
 а Правильний трикутник: S=
а Правильний трикутник: S=![]() а2.
а2.
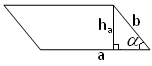
Трапеція ( а, b−основи трапеції, h−висота трапеції).
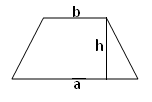
S=![]() (а+b)h.
(а+b)h.
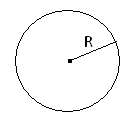 Площа круга та його частин.
Площа круга та його частин.
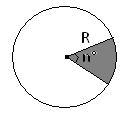
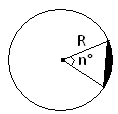
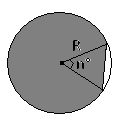
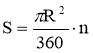 −площа кругового сектора, що відповідає центральному куту в n°.
−площа кругового сектора, що відповідає центральному куту в n°.
S=πR2−площа круга
Круговий сегмент : 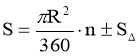


про публікацію авторської розробки
Додати розробку

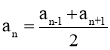 , де n≥2, nєΝ.
, де n≥2, nєΝ.
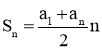 або
або 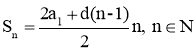
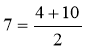
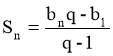 або
або 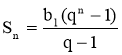
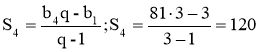
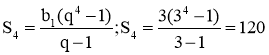
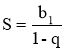 .
.
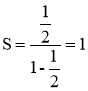 .
.
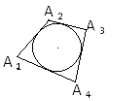
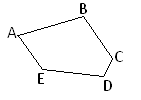 АВСDЕ−опуклий многокутник
АВСDЕ−опуклий многокутник

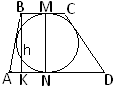 M N=h
M N=h