Опорні схеми для використання на уроках геометрії в 7 класі

ОПОРНІ СХЕМИ ДЛЯ ВИКОРИСТАННЯ НА УРОКАХ ГЕОМЕТРІЇ В 7 КЛАСІ

Писарєва Алла Володимирівна,

учитель математики Ліцею №5

імені Т.Г.Шевченка

Коростишівської міської ради

Уміння розв’язувати задачі – таке саме практичне мистецтво,

як уміння плавати й бігати. Ним можна оволодіти

тільки шляхом наслідування та вправ.

                                                          Д. Пойа

        Під час навчання геометрії учні знайомляться з основними геометричними поняттями, їх властивостями, починають розв’язувати найпростіші геометричні задачі. З вивченням все більшого обсягу геометричного  матеріалу вони зіштовхуються  з першою проблемою:  маючи деякі знання  (вивчивши правила), не знають, як їх застосовувати (не можуть розв’язати задачу).

Практика показала, що інформація, подана у вигляді певних моделей, алгоритмів, схем та асоціацій краще запам’ятовується; використання таких прийомів розвивають в учнів логічне мислення, краще формуються практичні уміння й навички.

Успішне оволодіння саме геометричними навиками базується на таких «трьох китах»:

1.                знання означень, властивостей геометричних фігур та теорем;
2.                уміння зобразити дані фігури та її властивості на рисунку;
3.                уміння впізнати на малюнку певний геометричний факт, його властивості.

Наприклад, розглянемо медіану трикутника.

Учень повинен:

1.                знати таке означення: медіана трикутника – це відрізок, який з’єднує вершину трикутника з серединою протилежної сторони (або відрізок, який виходить з вершити трикутника та ділить протилежну сторону навпіл);
2.                вміти зобразити медіану трикутника на малюнку;
3.                за даними на запропонованому малюнку:

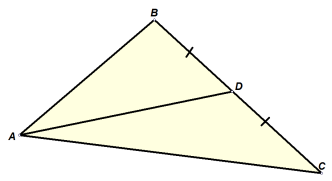
учень повинен дати назву відрізку АD (АD – медіана трикутника АВС).

  *     *    *

 Головним орієнтиром для пошуку ідеї розв’язання геометричної  задачі є така схема:

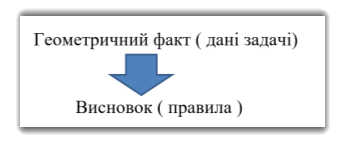
Зробивши логічний висновок за такою схемою, учні просунуться до розв’язку задачі.

Кожний геометричний факт  зображується у вигляді такого ж логічного ланцюжка, який містить стрілочки:     →      - слідує (випливає),         ↔            - рівносильність. У таких ланцюжках уже спостерігається логіка: що випливає з того чи іншого геометричного факту. Розглянемо приклади.

Поняття «середина відрізка» часто зустрічається в геометрії і несе теоретичне і практичне навантаження, оскільки міститься у таких геометричних поняттях: медіана трикутника, середня лінія трикутника та трапеції, діаметр кола тощо. Тому учням потрібно розуміти його зміст, вміти позначити на малюнку і використати для розв’язання задачі. Засвоєнню цих вимог сприяє така схема (логічний ланцюжок):

Середина відрізка ↔  Відрізок ділиться навпіл → Два рівних відрізки

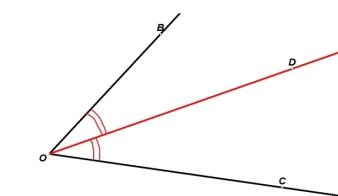
 Наприклад, для бісектриси кута аналогічна схема:

Бісектриса кута   ↔    Кут ділиться навпіл   →     Два рівних кута

          Розглянемо застосування таких прийомів при вивченні теми «Коло, дотична до кола», геометрія, 7 клас.

1.                Аналіз.

Основні знання з теми (перелік правил, які повинен знати учень):

1.               Коло, елементи кола, їх властивості.
2.               Дотична до кола перпендикулярна до радіуса, проведеного в точку дотику.
3.               Відрізки дотичних, проведених до кола з однієї точки, рівні.

Орієнтири для розв’язування задач:

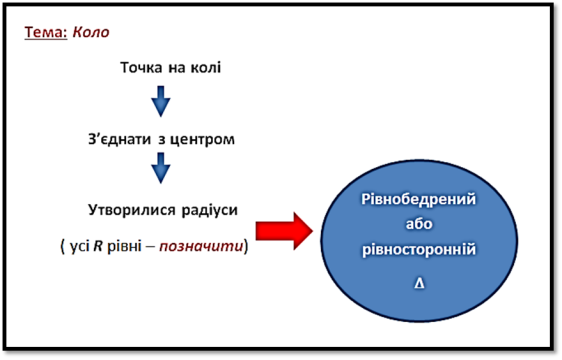
1.               Усі точки кола, які даються в задачі, з’єднати з центром → отримали радіуси.
2.               Усі радіуси кола рівні → позначити рівні радіуси на малюнку → можливе утворення рівнобедреного або рівностороннього трикутника.
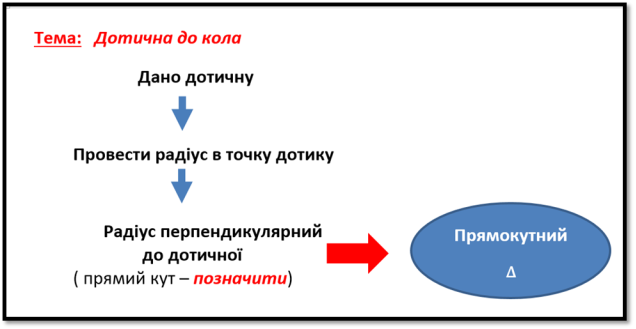
3.               Якщо дано дотичну до кола, то позначити її властивість (радіус, проведений в точку дотику, перпендикулярний до дотичної) → можливе утворення прямокутного трикутника.

2.                Подача опорної схеми.  Зазначені в орієнтирах логічні ланцюжки можна спростити і подати у вигляді схеми, яка приведе до розв’язання задачі:    

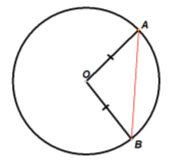
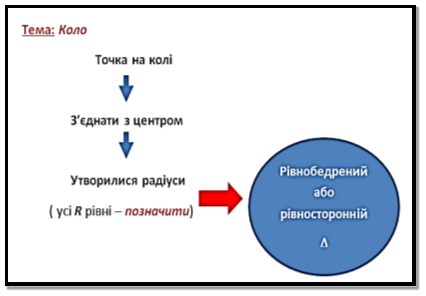
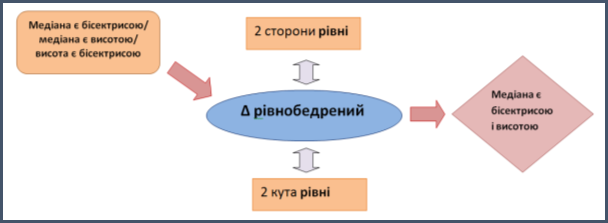
Для утвореного, наприклад, рівнобедреного трикутника у відповідній темі діти вже опрацювали таку опорну схему:

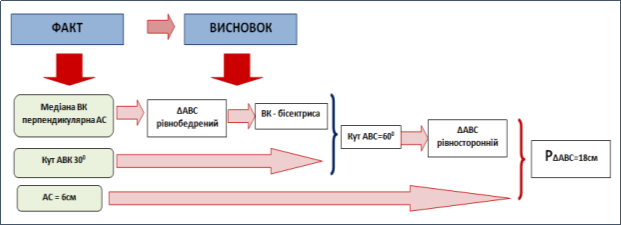
Приклад застосування орієнтиру «Факт – Висновок» та опорної схеми для розв’язування задачі показано на схемі:

Задача:  У трикутнику АВС медіана ВК перпендикулярна до сторони АС, довжина якої  дорівнює 6 см. Знайти периметр трикутника АВС, якщо кут АВК дорівнює 30^о.

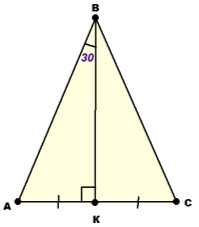
Дуже важливий візуальний супровід: рисунок до задачі з відповідними позначками.

МАТЕРІАЛИ ДЛЯ ВИКОРИСТАННЯ У 7 КЛАСІ

Тема: ВЗАЄМНЕ РОЗМІЩЕННЯ ПРЯМИХ НА ПЛОЩИНІ

Паралельність прямих

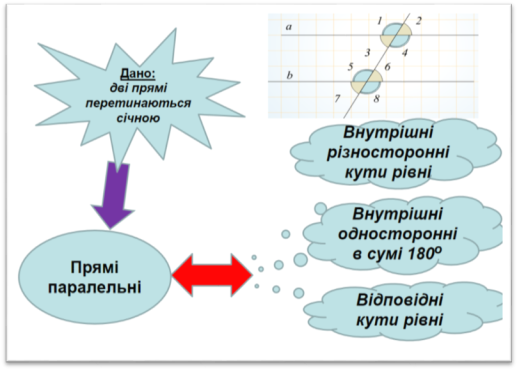
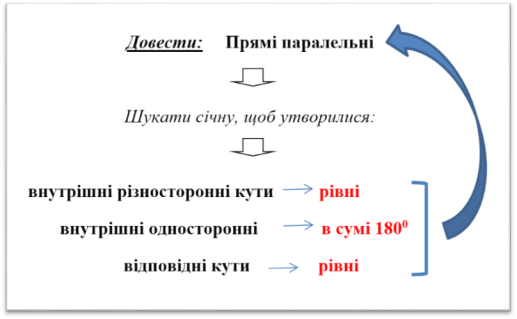
        Орієнтир для розв’язування задач:

     Тема: ТРИКУТНИКИ. ОЗНАКИ РІВНОСТІ ТРИКУТНИКІВ

Рівнобедрений трикутник

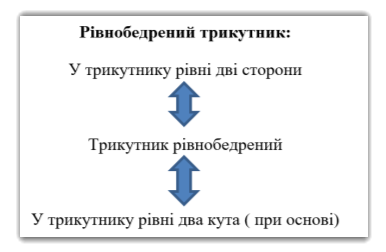
Прямокутний трикутник

Орієнтири для розв’язування задач на прямокутний трикутник:

1.                Дано кут 30⁰ → протилежний катет дорівнює половині гіпотенузи.
2.                Дано кут 60^о →другий гострий кут дорівнює 90^о – 60^о = 30^о → протилежний катет дорівнює половині гіпотенузи.
3.                Дано кут 45^о → другий гострий кут дорівнює 90^о – 45^о = 45^о → трикутник рівнобедрений → два катети рівні.

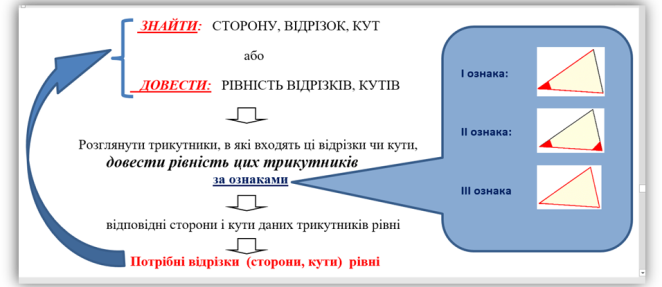
Ознаки рівності трикутників

Орієнтири для розв’язування задач:

    Тема: КОЛО І КРУГ

Орієнтири для розв’язування задач

Тема: КОЛО І ТРИКУТНИК

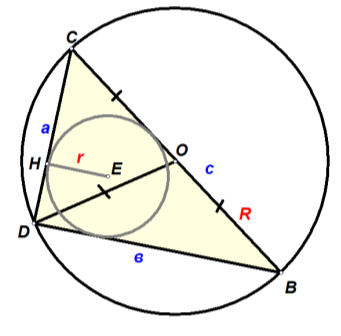
Основні знання з теми:

1. Центром вписаного у трикутник кола є точка перетину  його бісектрис.
2. Центром описаного навколо  трикутника кола є точка перетину серединних перпендикулярів, проведених до його сторін.
3. Прямокутний трикутник, вписаний в коло:

• Гіпотенуза є діаметром.
• Радіус дорівнює половині гіпотенузи.
• Медіана дорівнює  половині гіпотенузи

4. Прямокутний трикутник, описаний навколо кола:

• Відрізки дотичних рівні.
• 2r = а + в – с

 .