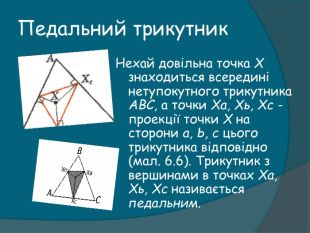
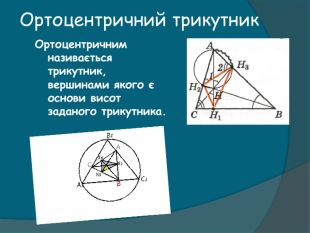
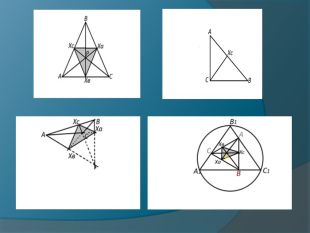
Презентація "Цікаві трикутники (з історії геометрії)"

З ІСТОРІЇ ГЕОМЕТРІЇЦікаві трикутники

Мета1 Дослідження властивостей та особливостей трикутників різного виду.2. Поглиблене вивчення означень та ознак трикутників. Виходячи із мети у дослідженні сформовані такі завдання:1.1 Розтлумачити особливості трикутників різного виду.1.2 Поглибити знання про визначні точки в довільному трикутнику.1.3 На прикладах задач чітко сформувати особливості та ознаки трикутників.1.4 Пояснити історичний зміст виникнення трикутників.

Об’єктом дослідження є такі види трикутників: педальний,ортоцентричний, різницевий,серединний, медіанний, цілочисловий, Піфагорів та трикутник Наполеона. Робота складається із вступу трьох розділів, висновку та додатків. Кожен розділ розкриває значеня та пояснює види трикутників.

Трикутник – один з найпотужніших і універсальних символів. Рівносторонній трикутник – представляє божество, вогонь, життя, серце, гору і сходження, благополуччя, гармонію і королівську владу. Трикутники, що перетинаються, утворюючи гексаграму, символізують синтез, союз протилежностей. Як найпростіша плоска фігура, що має за основу число 3, трикутник був піфагорським знаком мудрості, зв'язаним з богинею Афіною. В індуїзмі і християнстві трикутник – знак Бога. Бог християнської Трійці інколи представлений оком у середині трикутника чи фігурою з трикутним німбом. У загальному розумінні трикутники чи композиції, що містять форму трикутника, можуть позначити тріади богів чи інші троїсті поняття.

Педальний трикутник Нехай довільна точка X знахо­диться всередині нетупокутного трикутника АВС, а точки Ха, Хь, Хс - проекції точки X на сторони а, Ь, с цього трикутника відповід­но (мал. 6.6). Трикутник з верши­нами в точках Ха, Хь, Хс нази­вається педальним.

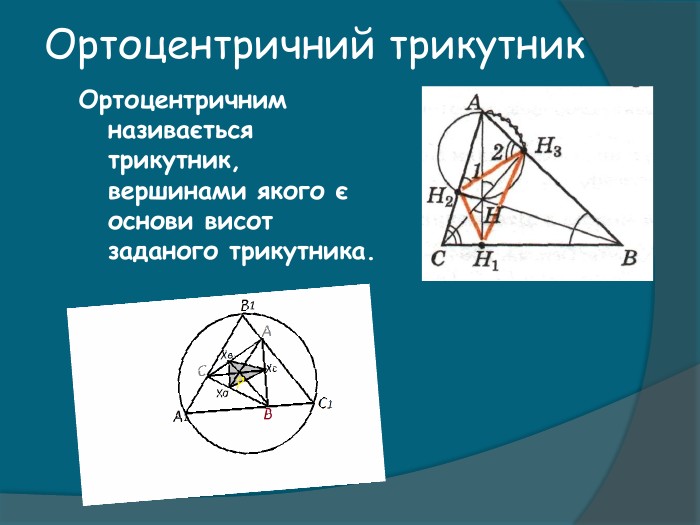
Якщо точка Х збігається з ортоцентром Х1 Х2 Х3, то вона є центром кола, описаного навколо АВС (мал.2) Доведеня. Продовжимо ХХ1 , ХХ2, ХХ3 до перетину зі сторонами Х1 Х2 Х3.оскільки точках Х- ортоцентр Х1 Х2 Х3,то сторони цього трикутника паралельні відповідним сторонам АВС, а чотирикутники АХ2 Х1 Х3 , ВХ1 Х2 Х3,С Х2 Х3 Х1- палалелограми і відрізки АХ1, ХХ2,ХХ3 належать серединним перпендикулярам до сторін ВС,АС,АВ. Отже ,точка Х є центром кола, описаного навколо АВС. Задача1

Задача 3 Якщо дві з чудових точок трикутника збігаються,то трикутник АВС- рівносторонній (мал.5) Доведення. Нехай, наприклад, збігаються точки ОіН. Проведемо висоту АН. Оскільки,їй належить точка О, то відрізок ОН,поділяє хорду ВС навпіл, і висота АН, є медіаною значить,АС=АВ аналогічно доводиться,що АВ=ВС.отже,АС=АВ=ВС, тому АВС-рівносторонній

Ортоцентричний трикутник. Ортоцентричним називається трикутник, вершинами якого є основи висот заданого трикутника.

Цілочисловий та Піфагорів трикутник Цілочисловим називається трикутник, довжини сторін якого виражаються натуральними числами. Та­ких трикутників безліч. Усі трійки натуральних чисел, які задовольняють умову нерівності для сторін трикут­ника, можуть бути довжинами сторін цілочислового трикутника. Якщо цілочисловий трикутник є прямокутним, то його називають піфагоровим трикутником. Наприк­лад, піфагоровими є єгипетські трикутники, довжини сторін яких пропорційні 3, 4 і 5 одиницям виміру.

Необхідною і достатньою умовою того, щоб цілочисловий трикутник із довжинами сторін х, у, 2 був піфагоровим, є виконання співвідношеннях2 + у2 = г2. Це випливає безпосередньо з теореми Піфагора і оберненої до неї. Зрозуміло, якщо трійка чисел {х, у, г} задовольняє вказане рівняння, то задовольняє його і кожна трійка {іх, {у, іг], де і - довільне натуральне число. Піфагорів трикутник називається основним., якщо довжини його сторін х, у, г - числа взаємно прості (тобто не мають спільних множників). Піфагор знайшов, що трійки чисел {2п + 1; 2п2 + + 2п; 2п2 + 2п + 1}, п е N. задовольняють рівняння (2п + І)2 + (2п2 + 2п)2 = (2п2 + 2п + І)2, тобто визна­чають піфагоровий трикутник.

Серединний трикутник. Серединним трикутником даного трикутника нази­вають трикутник, вершинами якого є середини сторін за­даного трикутника.

Єгипетський трикутник Землеміри Стародавнього Єгипту для побудови прямого кута користувались таким способом. Мотузок ділили вузлами на 12 рівних частин і кінці зв'язували. Потім мотузок розтягували на землі так, щоб утворився трикутник зі сторонами 3,4 і 5 поділок. Кут трикутника, протилежний до сторони, яка має 5 поділок, був прямий (32 + 42 = 52). У зв'язку з таким способом побудови прямого кута трикутник із сторонами 3, 4, 5 од. називають єгипетським

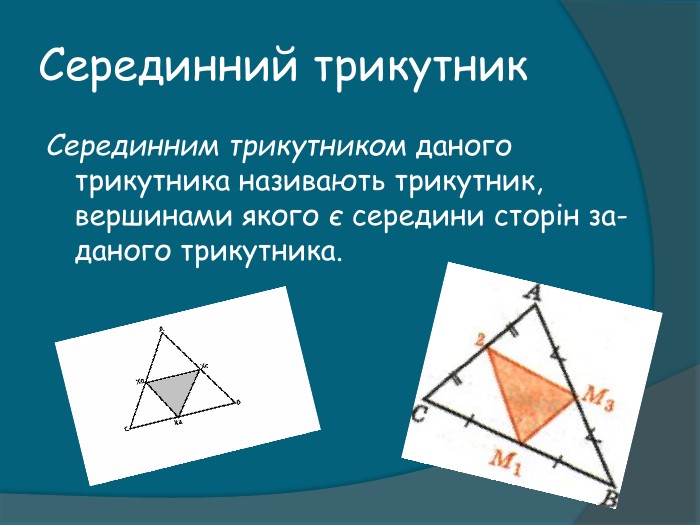
Слово про медіани довільного трикутника Нехай маємо трикутник АВС зі сторонами а, b,c тоді медіанним трикутником назвемо трикутник зі сторонами, які дорівнюють медіанам mа,m,, mc даного трикутника АВС. Визначемо властивості медіанного трикутника, які здаються корисними та важливими для ерудиції учнів, зацікавлених математикою.

Трикутники Наполеона та кола Торрічеллі Якщо на сторонах трикутника побудувати правильні трикутники, то отримаємо конфігурацію з чотирьох трикутників, які називають трикутниками Наполеона. Кола, описані навколо побудованих правильних трикутників, називають колами Торрічеллі . Вважають, що саме Наполеон Бонапарт (французький імператор) вивчав цю конфігурацію і першим сформулював та довів твердження, яке носить назву теорема Наполеона: “ Якщо на сторонах довільного трикутника зовні нього побудовано рівносторонні трикутники, то їхні центри є вершинами рівностороннього трикутника ”

Торрічеллі Еванджеліста (1608–1647)Італійський фізик і математик у математиці удосконалив і широко застосував метод неподільних при рішенні завдань на дотичні. Використовував кінематичні уявлення, зокрема принцип складання рухів. Узагальнив правило квадратури параболи на випадок довільного раціонального показника. Самостійно, хоч і декілька пізніше {Ж. Роберваля}, визначив квадратуру циклоїди. Услід за {Р. Декартом} знайшов довжину дуги логарифмічної спіралі. Торрічеллі належать також роботи по математиці (зокрема, розвинув метод неподільних) і балістиці, удосконаленню оптичних приладів, шліфовці лінз.

Піфагор Народився близько 580 р. до н. е. на острові Самос. Видатний грецький вчений, математик і метеоролог.

Висновки Працюючи та досліджуючи наукову роботу я прийшла до таких висновків: Всі трикутники мають власні особливості та відмінності. Безліч теорем, що стосуються особливих видів трикутників грунтуються на твердженнях стосовно трикутника загального виду. Задачі пов’язані з особливими видами трикутників мають важливе значення у розвитку геометрії трикутника. Матеріали даної роботи можуть бути використані на уроках математики, також гурткових та факультативних заняттях