Опорні схеми з математики для 6 класу "Вивчаємо математику за допомогою схем"

Множення звичайних дробів

 

 

1.        

 

 

 

 

 

2.        

 

 

 

 

 

3.        

 

 

 

 

 

 

 

Ділення звичайних дробів

 

 

1.              

 

 

 

 

2.              

 

 

 

 

 

 

 

 

 

 

3.        

 

 

Перетворення звичайних дробів у десяткові

 

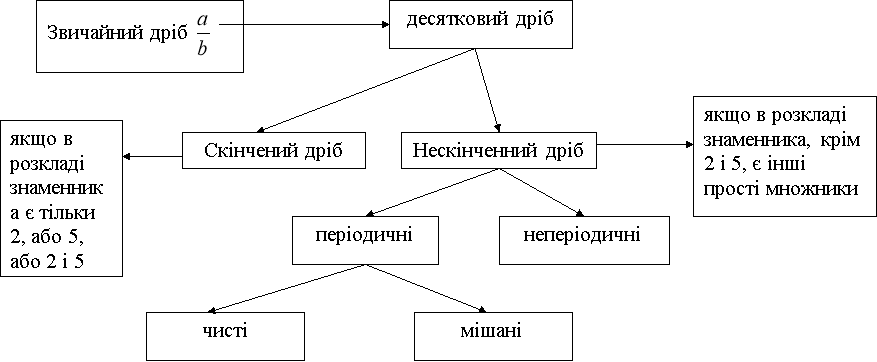
a:b

перевести

 

 

 

 

 

 

 

 

 

 

 

 

 

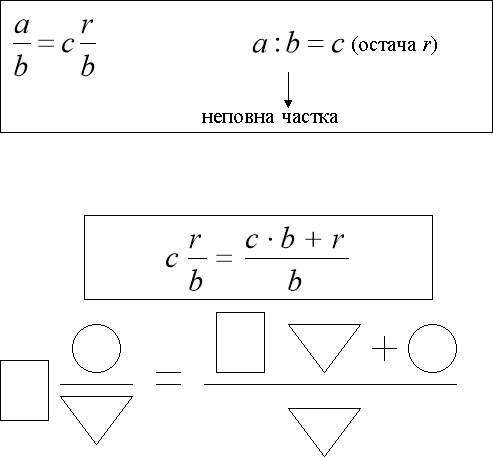
Виділення цілої частини із неправильного дробу

 

 

 

 

 

 

 

Перетворення мішаного числа у неправильний дріб

 

 

 

 

 

 

 

 

 

 

 

 

Основні властивості дробу

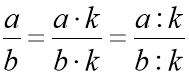, де k – натуральне число

Правила знаходження

НСД        НСК

 

 

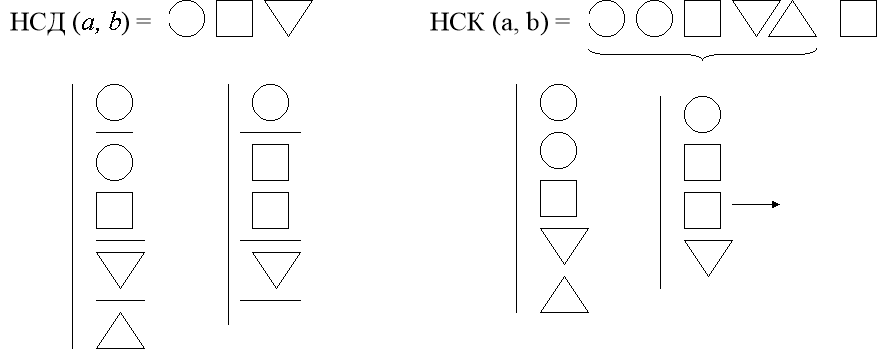
a

a   b      a   b

 

 

 

немає у розкладі числа а

 

 

 

 

Дописуємо ті прості множники, яких не вистачає у розкладі першого числа а

 

 

 

 

 

 

 

 

Знаходження числа за його дробом

 

 

 

 

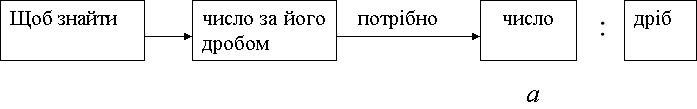
Схема задачі на знаходження числа за його дробом

 

 

 

 

 

 

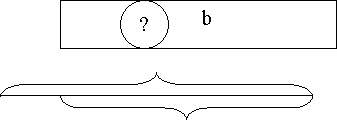
– задана дробом

а – задана по іменованою величиною

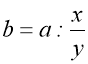
Приклад. На заняттях у класі 28 учнів, що становить кількості учнів класу. Скільки учнів у класі?

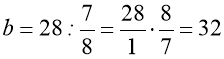(учні)

Знаходження дробу від числа

 

 

 

 

 

Схема задач на знаходження дробу від числа

 

 

 

 

 

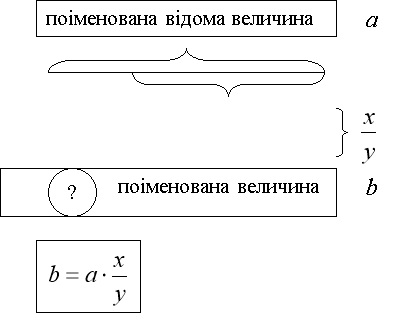
задана частина

величини дробом

 

 

 

 

 

 

 

 

 

Приклад. Знайти від 159 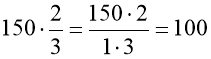км.

(км).

Взаємно обернені числа

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

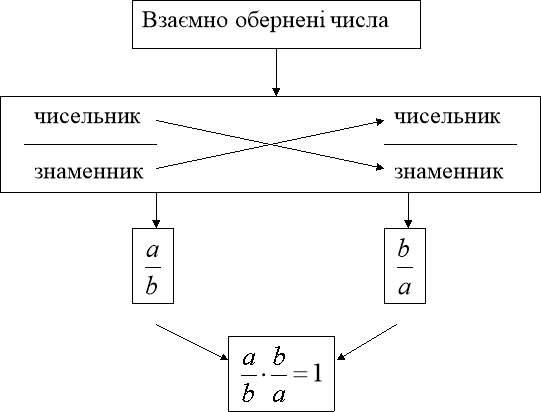
Приклади.

 

 

2 і ;    5 і ;     і – взаємно обернені

 

Обернена пропорційність

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

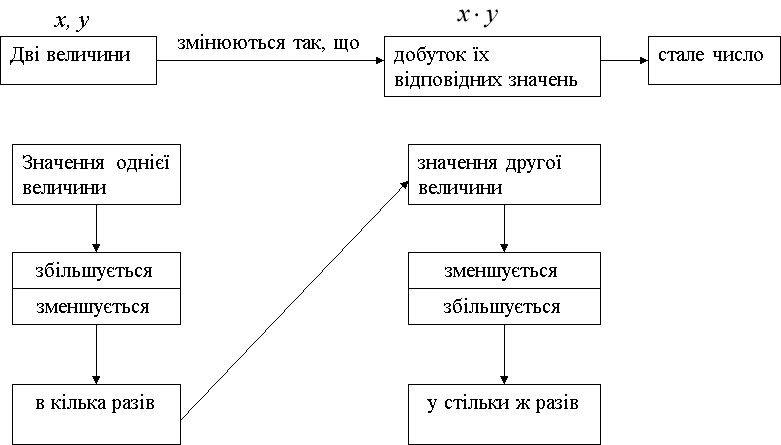
Пряма пропорційність

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

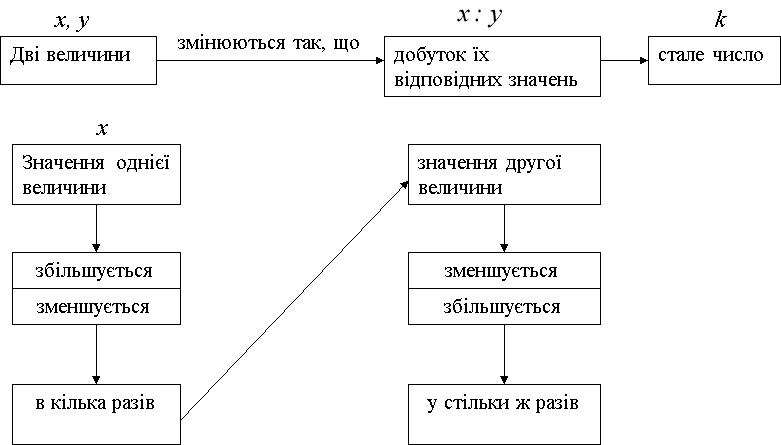
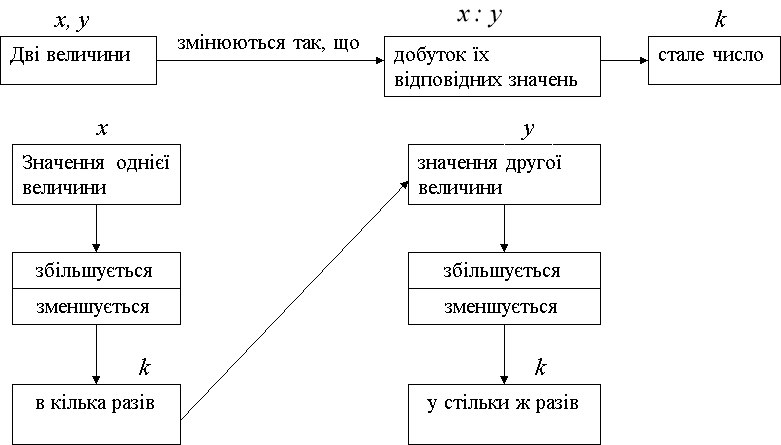
Пропорція та її властивості

Означення. Рівність двох відношень називається пропорцією.

 

Загальний вигляд пропорції

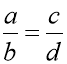або

 

a, d – крайні члени пропорції;

b, c – середні члени пропорції.

 

 

Основні властивості пропорції:

 

1.                                                                                 – добуток крайніх членів пропорції дорівнює добутку середніх членів;
2. У пропорції можна міняти місцями середні члени між собою, крайні, середні і крайні одночасно:

із 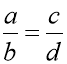можна одержати: , .

 

 

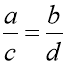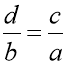Перпендикулярні прямі

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

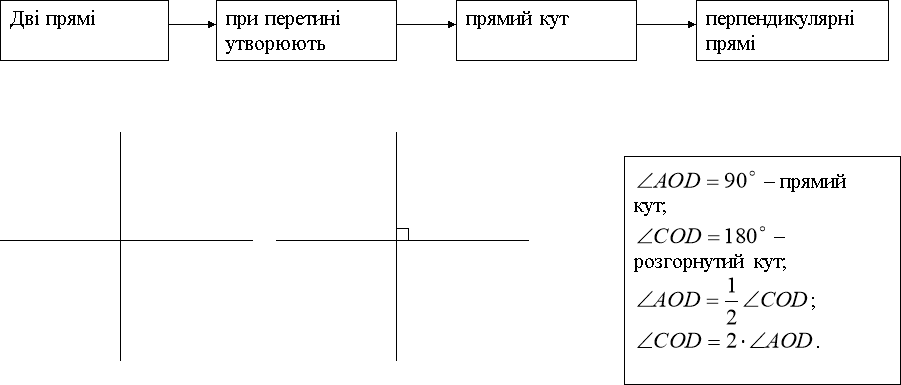
  , то

Паралельні прямі

 

 

 

 

 а       A    B

 

 b       C    D

 

          

Властивості

               c  b

 

 

              a

 

 

               a  M

 

               b

 

 

Взаємне розміщення двох прямих на площині

 

 

 

 

 

 

 

 

 

 

 

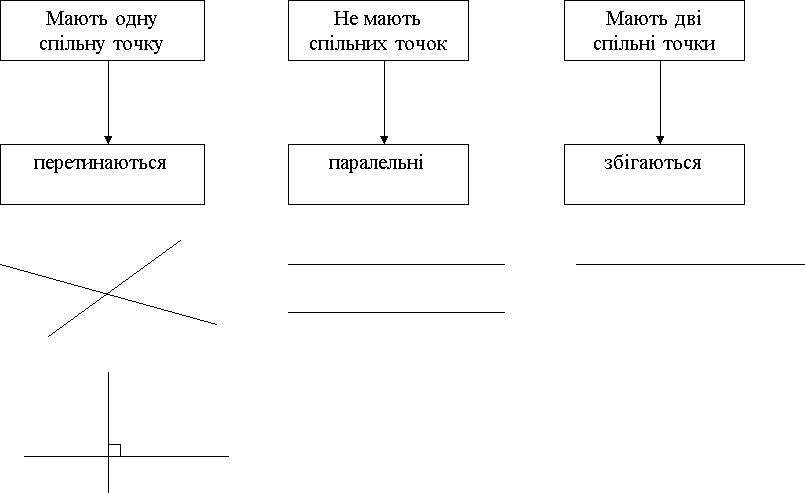
 a       a      a A B b

 

 

  b      b

     

   a      

 

 

  b

       

 

Трикутник

Види трикутників в залежності від величин кутів

  В     А       А

 

 

 

 

 

А    С          В      С  В    С

  Гострокутний     Тупокутний    Прямокутний

 

Види трикутників в залежності від довжини сторін

  В       В      В

 

 

 

 

 

А     С  А     С        А    С

Різносторонній    Рівносторонній    Рівнобедрений

 

В       Площа трикутника

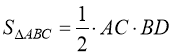
        AC = a; BD = h;

А  D     С  .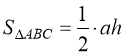

 

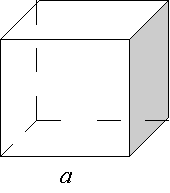
Куб                     , де а – довжина ребра             Граней – 6 (квадрати) Вершин –8 Ребер – 12

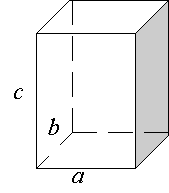
Прямокутний паралелепіпед   a, b, c – виміри (виходять з однієї вершини)   a – довжина; b – ширина; c – висота                     Граней – 6 (прямокутники) Ребер – 12 Вершин – 8

 

Конус

 

 

 

 

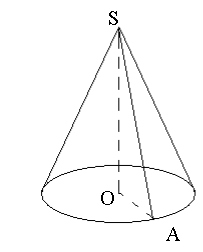
O – центр основи конуса;

S – вершина конуса;

 

– висота конуса;

– радіус основи конуса;

– твірна

конуса

 

 

 

 

 

 

 

 

 

 

 

 

 

Циліндр

 

 

 

 

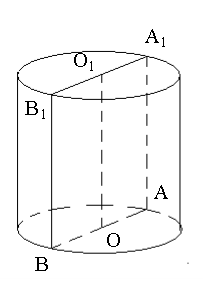
О, О₁ – центри основ

Основа – круг

 

– висота циліндра

ВВ₁, АА₁ – твірні

– радіус основи

 

 

 

 

 

 

 

 

 

 

 

 

 

 

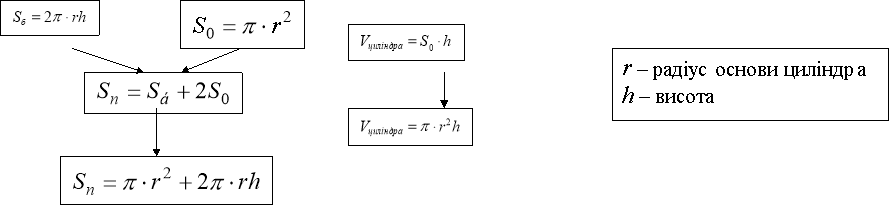
Круглі тіла

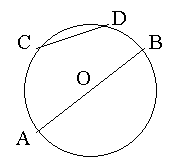
Коло

 

 

О – центр кола;

АО, ВО – радіуси; ;

АВ – діаметр; ;

С – довжина кола; CD – хорда

 

 

 

, де

 

 

Круг

 

 

 

 

 

 

 

 

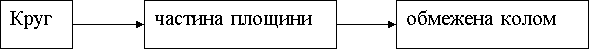
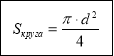
Координатна пряма

 

 

 

 

 

 

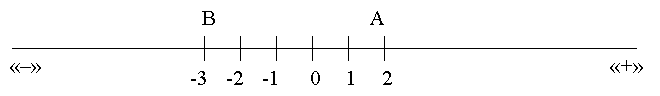
А(2)

В(-3)

 

 

 

 

 

 

 

 

 

 

 

 

 

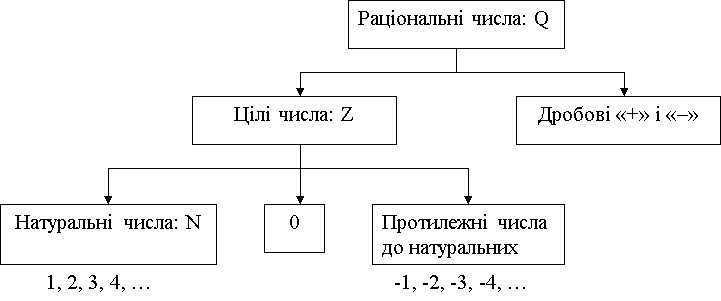
Модуль числа

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

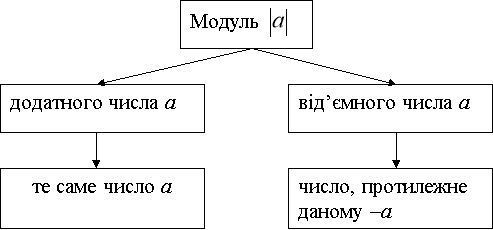
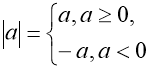
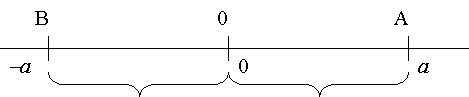
ОА=ОВ;   

Порівняння раціональних чисел

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

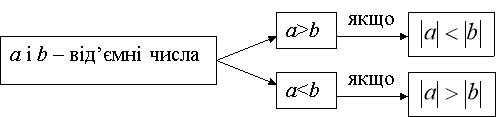
, бо

, бо

Координатна площина

 

 

 

 

 

 

 

 

 

 

 

 

Ох – вісь абсцис

Оу – вісь ординат

О – початок координат

 

 

 

 

 

 

 

 

 

 

 

Додавання раціональних чисел

Правила додавання раціональних чисел

1. Два від’ємні числа

 

 

 

 

2. Два додатні числа

 

 

 

 

3. Два числа з різними знаками

 

 

 

 

 

 

Закони додавання

1. – переставний закон

2. – сполучний закон

3. – закон про нуль

 

Пам’ятка

– сума двох протилежних чисел дорівнює 0.

Віднімання раціональних чисел

 

 

 

 

 

 

 

 

 

 

 

Розкриття дужок

 

 

 

 

 

 

 

– не змінюємо

–змінюємо

 

Множення раціональних чисел

 

 

 

 

 

 

 

 

Закони множення

1. – переставний закон

2. – сполучний закон

3. – розподільний закон

4. – закон про нуль

5. – закон про одиницю

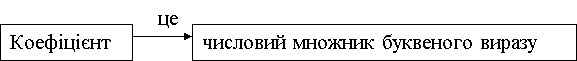Коефіцієнт

 

 

 

 

 

 

 

 

 

 

 

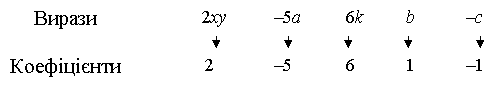
Ділення раціональних чисел

 

1.

 

 

 

 

 

2.

 

 

 

 

 

 

 

 

 

 

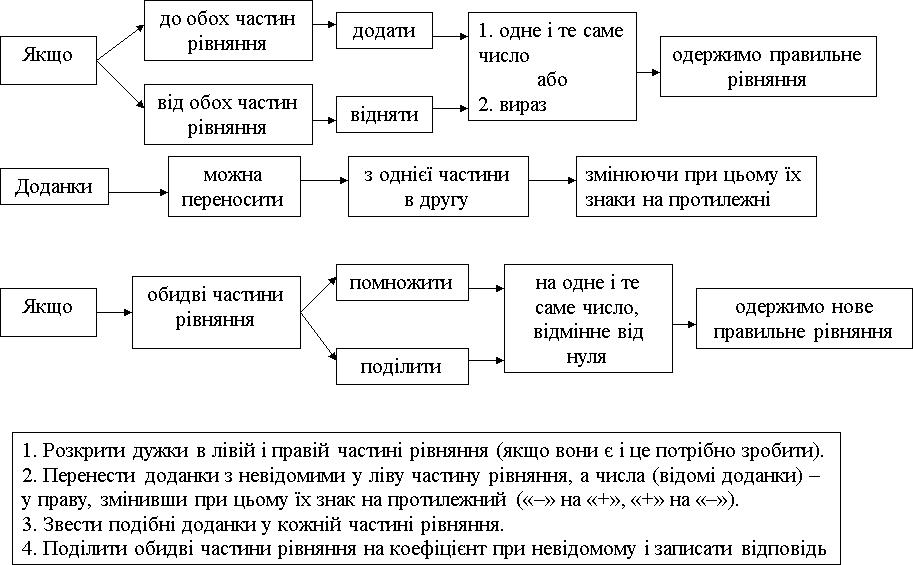
Основні властивості рівнянь

 

 

 

 

 

1.

 

 

 

 

2.

 

 

 

 

 

 

 

 

Схема розв’язання рівняння

 

 

 

 

 

 

 

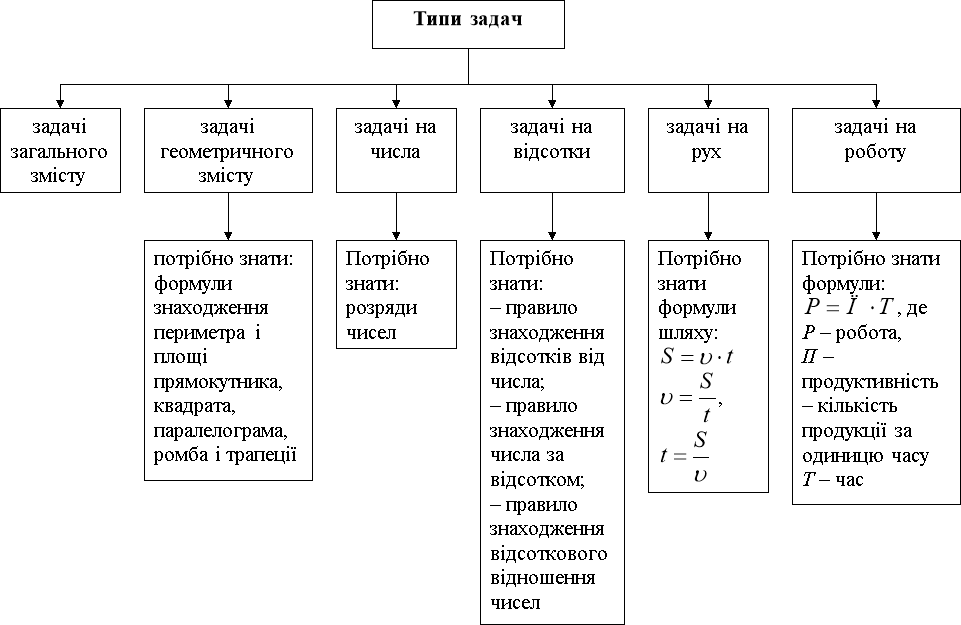
Задачі на складання рівнянь