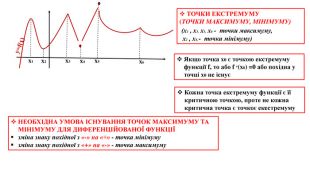
Опорні схеми з теми "Похідна функції"
Про матеріал
Дані опорні схеми є своєрідною "шпаргалкою" для учнів. Систематизовано і узагальнено навчальний матеріал з теми "Похідна функції". Подані і алгоритми знаходження точок екстремуму, проміжків зростання і спадання функції, найбільшого і найменшого її значення на проміжку. Даний матеріал буде корисним на уроках повторення у старшій школі та при підготовці учнів до ЗНО.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
-
-
Дякую за корисний матеріал!
pptx
До підручника
Алгебра і початки аналізу (академічний рівень) 10 клас (Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку

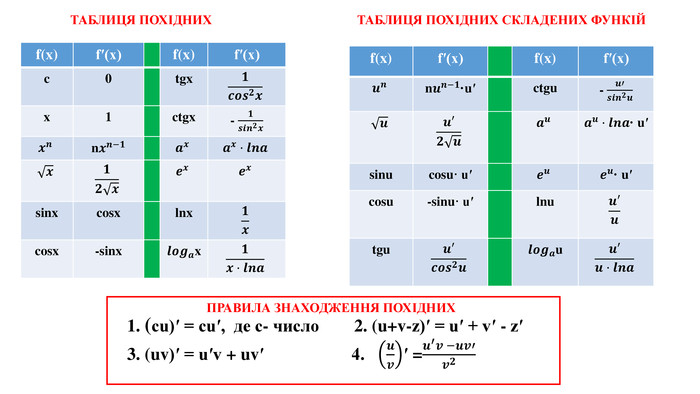
![y=f(x)Aαx0f(x0)y=kx+b. ГЕОМЕТРИЧНИЙ ЗМІСТ ПОХІДНОЇf ′(x0) = k= tgα (похідна функції y=f(x) у точці х0 дорівнює тангенсу кута між дотичною, проведеною до графіка функції у точці х0, і додатнім напрямом осі ОХ)УМОВИ ЗРОСТАННЯ (СПАДАННЯ) ФУНКЦІЇ y=f(x)якщо f ′(x)>0 для х є [а;в] - функція зростає на проміжку [а;в] якщо f ′(x)<0 для х є [а;в] - функція спадає на проміжку [а;в] МЕХАНІЧНИЙ ЗМІСТ ПОХІДНОЇs′(t) = v(t) v′(t)=a(t)s(t)- шлях v(t) – швидкість a(t) - прискорення КРИТИЧНІ ТОЧКИ – це внутрішні точки з області визначення, у яких похідна дорівнює нулю або не існує (у точках х1 , х2 похідна дорівнює нулю, у точці х3 – похідна не існує)y=f(x)x3x2x1 РІВНЯННЯ ДОТИЧНОЇ ДО ГРАФІКА ФУНКЦІЇ y=f(x) У ТОЧЦІ Х0y = f (x0) + f ′(x0)(x-x0) y=f(x)Aαx0f(x0)y=kx+b. ГЕОМЕТРИЧНИЙ ЗМІСТ ПОХІДНОЇf ′(x0) = k= tgα (похідна функції y=f(x) у точці х0 дорівнює тангенсу кута між дотичною, проведеною до графіка функції у точці х0, і додатнім напрямом осі ОХ)УМОВИ ЗРОСТАННЯ (СПАДАННЯ) ФУНКЦІЇ y=f(x)якщо f ′(x)>0 для х є [а;в] - функція зростає на проміжку [а;в] якщо f ′(x)<0 для х є [а;в] - функція спадає на проміжку [а;в] МЕХАНІЧНИЙ ЗМІСТ ПОХІДНОЇs′(t) = v(t) v′(t)=a(t)s(t)- шлях v(t) – швидкість a(t) - прискорення КРИТИЧНІ ТОЧКИ – це внутрішні точки з області визначення, у яких похідна дорівнює нулю або не існує (у точках х1 , х2 похідна дорівнює нулю, у точці х3 – похідна не існує)y=f(x)x3x2x1 РІВНЯННЯ ДОТИЧНОЇ ДО ГРАФІКА ФУНКЦІЇ y=f(x) У ТОЧЦІ Х0y = f (x0) + f ′(x0)(x-x0)](/uploads/files/81137/28178/28141_images/2.jpg)
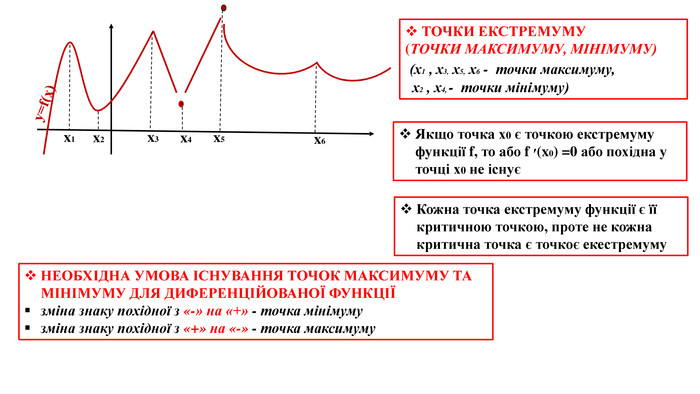
![АЛГОРИТМ ЗНАХОДЖЕННЯ ТОЧОК ЕКСТРЕМУМУ ТА ПРОМІЖКІВ ЗРОСТАННЯ (СПАДАННЯ) ФУНКЦІЇОбласть визначення функції. Критичні точки. Відкладання критичних точок та точок, що не входять в область визначення функції, на числовій прямій. Встановлення знаків похідної функції на отриманих проміжках (інтервалах). Запис відповіді. АЛГОРИТМ ЗНАХОДЖЕННЯ НАЙБІЛЬШОГО (НАЙМЕНШОГО) ЗНАЧЕННЯ ФУНКЦІЇ НА ПРОМІЖКУ [а;в] Область визначення функції. Критичні точки. Знаходження значень функції на кінцях відрізка [а;в] (у точках х=а, х=в) та у критичних точках, що належать відрізку [а;в]. Вибір з отриманих результатів найбільшого та найменшого значення. Запис відповіді: max f(x) = f(x1)= c min f(x) = f(x3)=d [а;в] [а;в] АЛГОРИТМ ЗНАХОДЖЕННЯ ТОЧОК ЕКСТРЕМУМУ ТА ПРОМІЖКІВ ЗРОСТАННЯ (СПАДАННЯ) ФУНКЦІЇОбласть визначення функції. Критичні точки. Відкладання критичних точок та точок, що не входять в область визначення функції, на числовій прямій. Встановлення знаків похідної функції на отриманих проміжках (інтервалах). Запис відповіді. АЛГОРИТМ ЗНАХОДЖЕННЯ НАЙБІЛЬШОГО (НАЙМЕНШОГО) ЗНАЧЕННЯ ФУНКЦІЇ НА ПРОМІЖКУ [а;в] Область визначення функції. Критичні точки. Знаходження значень функції на кінцях відрізка [а;в] (у точках х=а, х=в) та у критичних точках, що належать відрізку [а;в]. Вибір з отриманих результатів найбільшого та найменшого значення. Запис відповіді: max f(x) = f(x1)= c min f(x) = f(x3)=d [а;в] [а;в]](/uploads/files/81137/28178/28141_images/4.jpg)