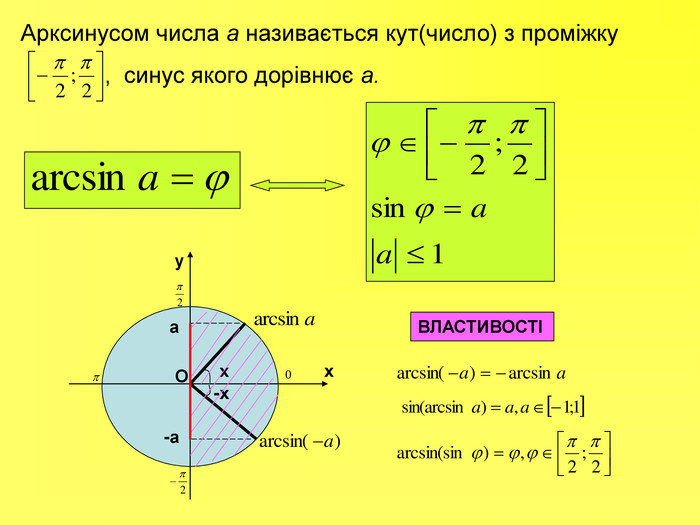
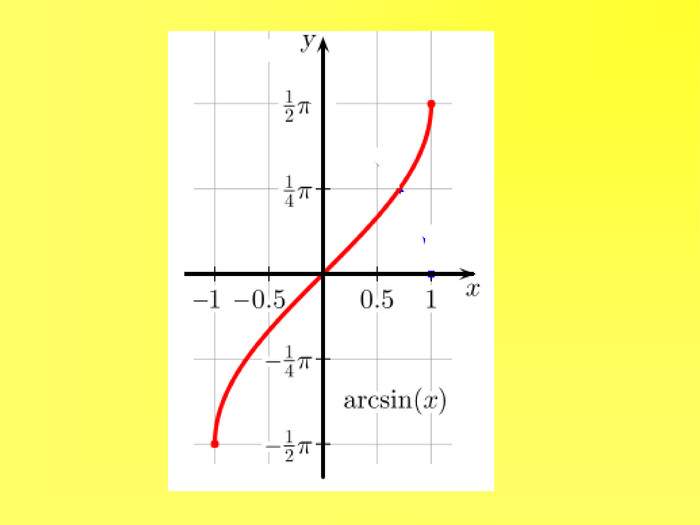
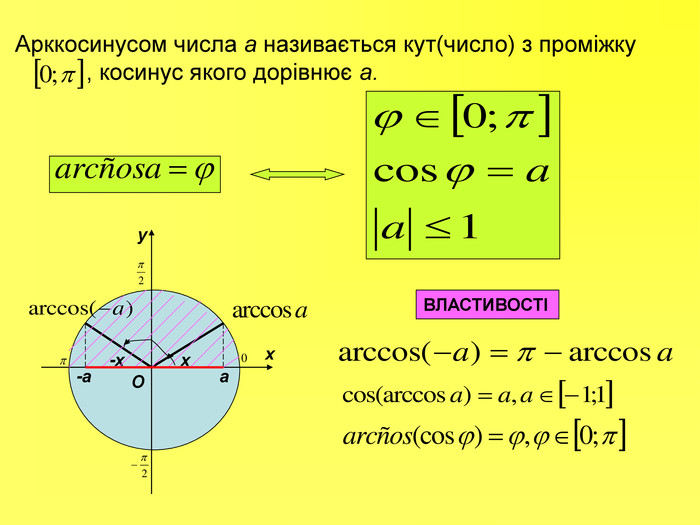
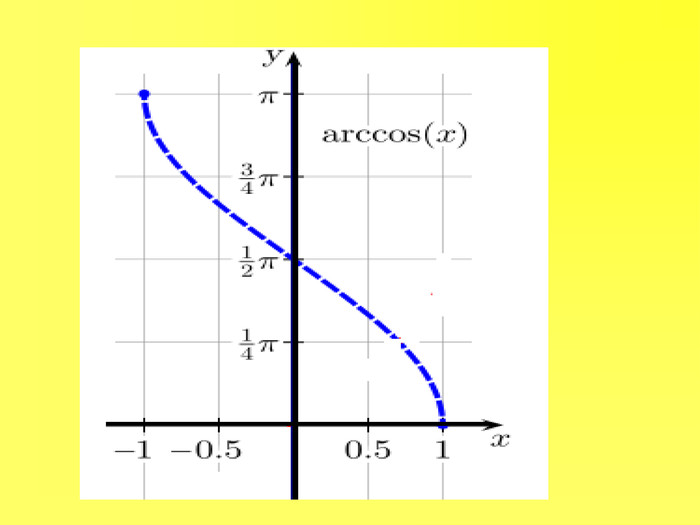
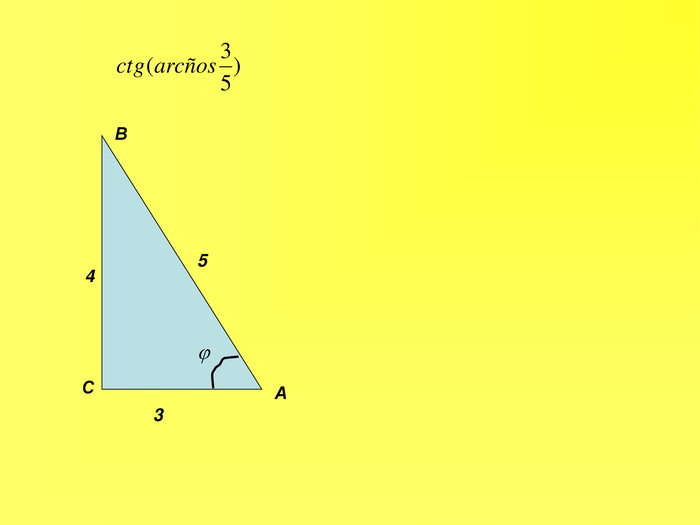
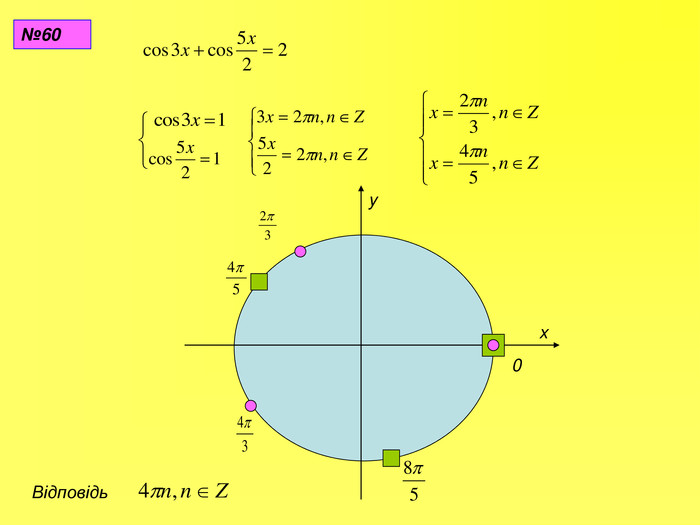
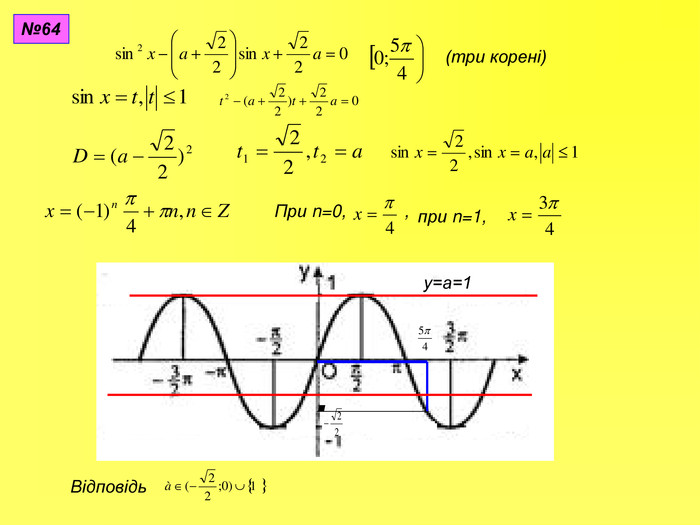
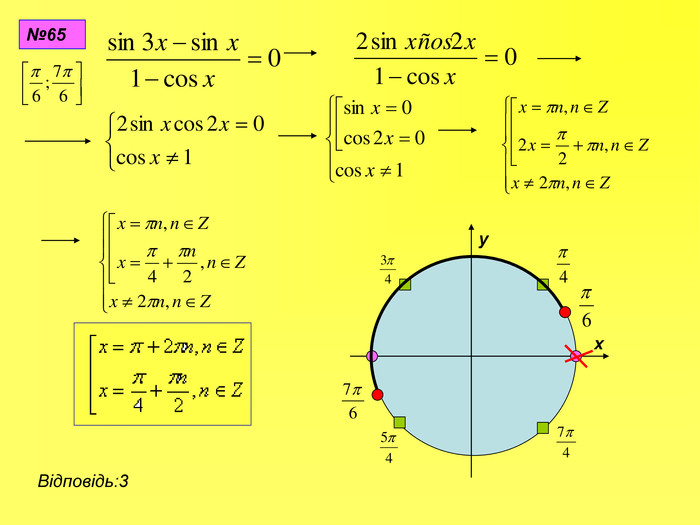
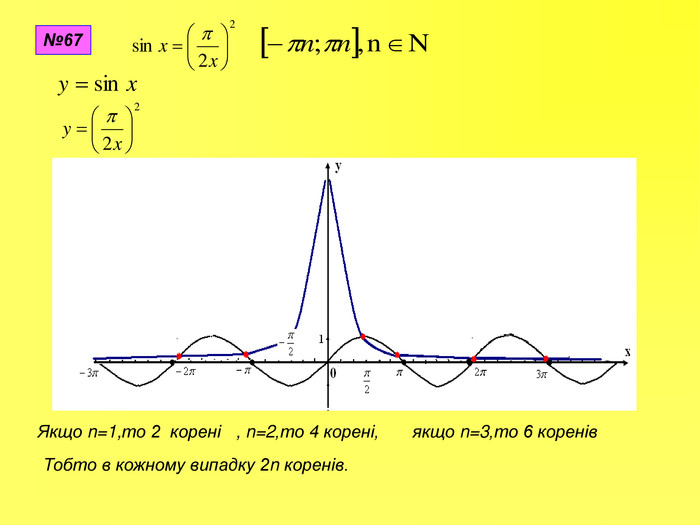
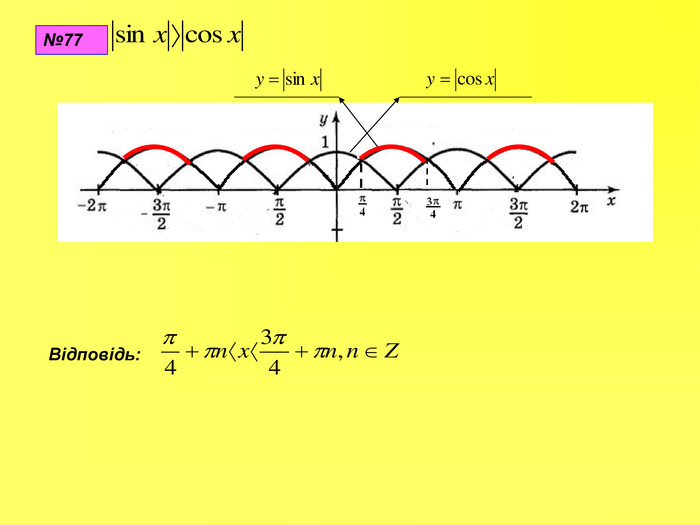
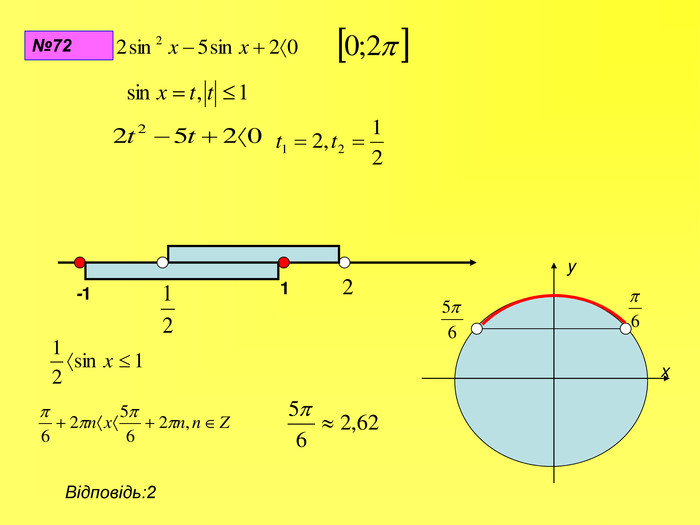
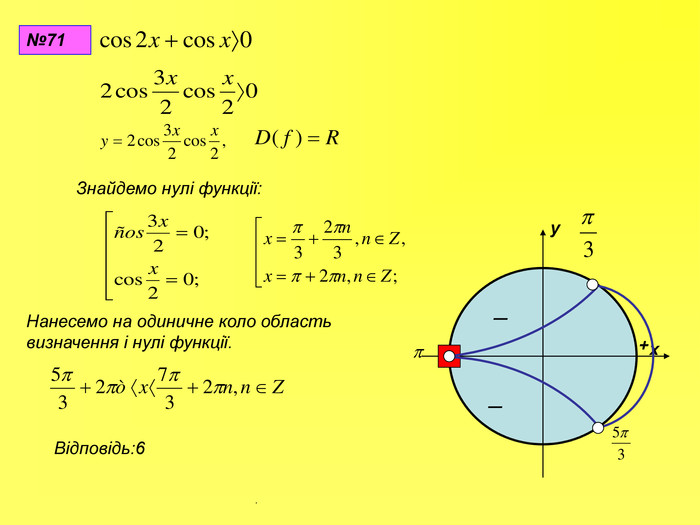
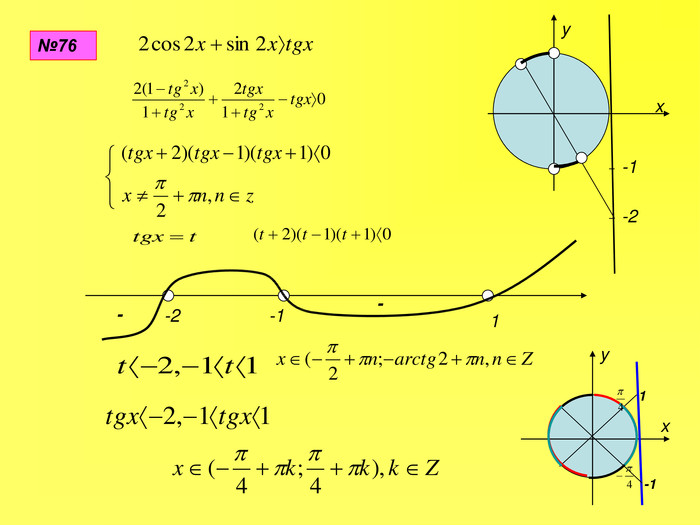
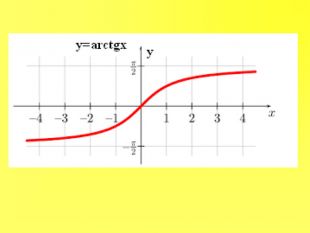
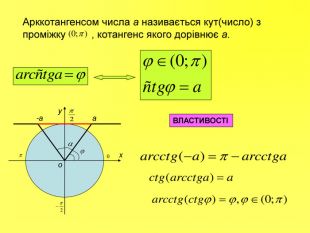
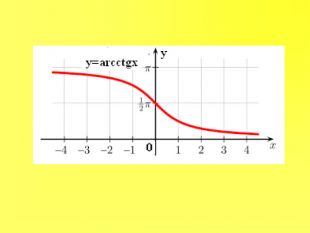
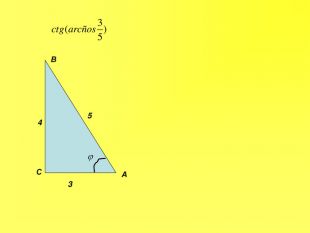
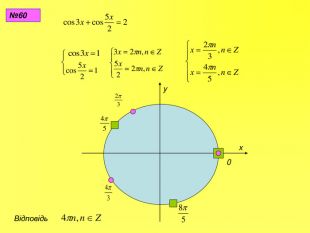
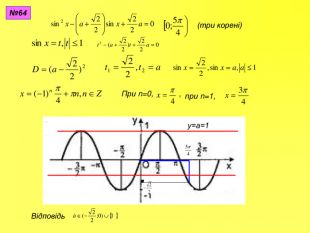
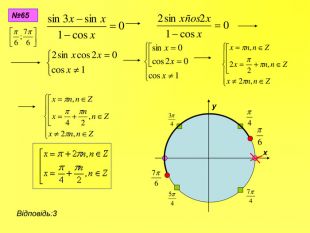
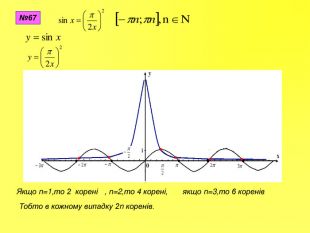
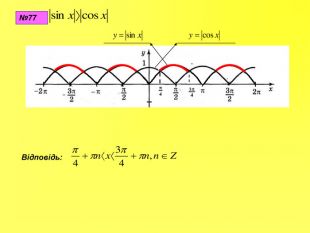
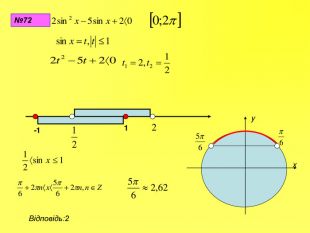
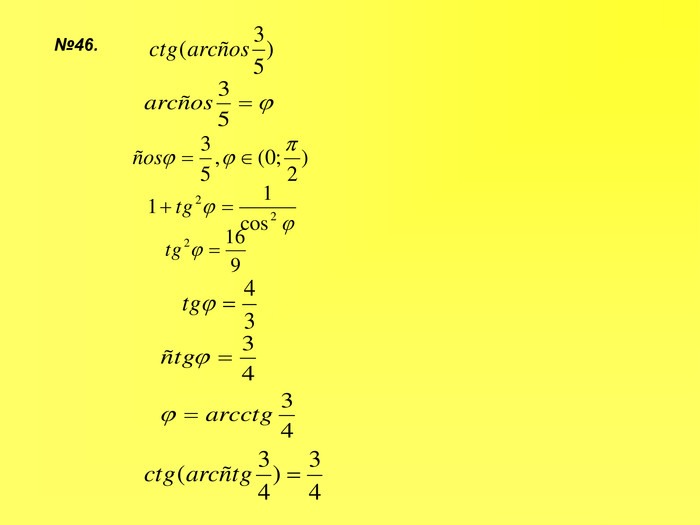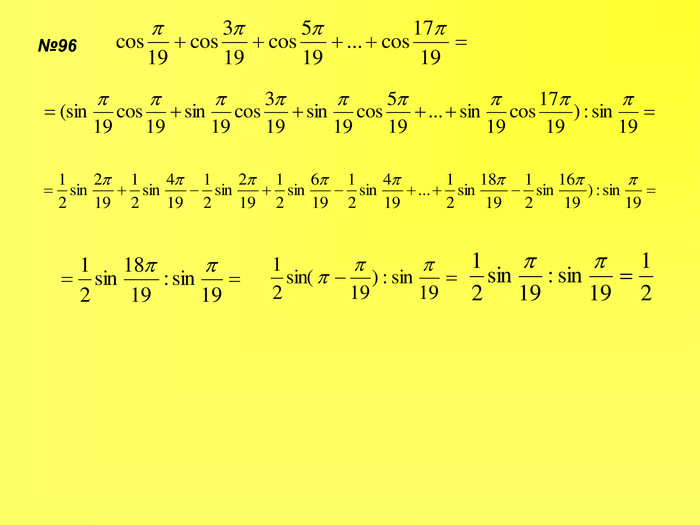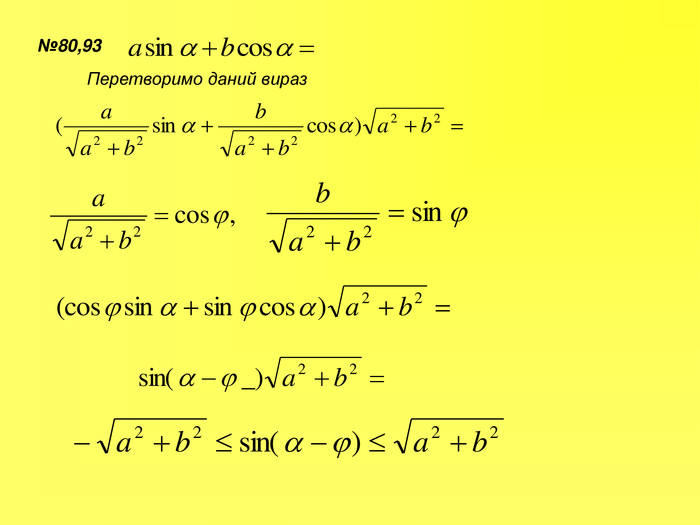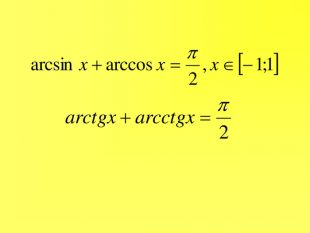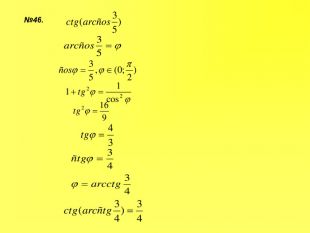Прентація до уроків з алгебри в 10 класі"Тригонометричні вирази та їх перетворення"
Прентація до уроків з алгебри в 10 класі"Тригонометричні вирази та їх перетворення"-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Тригонометричні вирази та їх перетворення
Арксинусом числа а називається кут(число) з проміжку , синус якого дорівнює а. а -а О х у х -х ВЛАСТИВОСТІ
Арккосинусом числа а називається кут(число) з проміжку , косинус якого дорівнює а. О х у -х х а -а ВЛАСТИВОСТІ
Арккотангенсом числа а називається кут(число) з проміжку , котангенс якого дорівнює а. х у о а -а ВЛАСТИВОСТІ
№46.
3 5 4 С А В
1
№86 №98 2 3
№96
№80,93 Перетворимо даний вираз
№81 Очевидно + №100
Тригонометричні рівняння і нерівності
№60 x y 0 Відповідь
№64 При n=0, , (три корені) при n=1, у=а=1 . Відповідь
№65 х у Відповідь:3
№67 Тобто в кожному випадку 2n коренів. Якщо n=1,то 2 корені , n=2,то 4 корені, якщо n=3,то 6 коренів
Нерівність називається тригонометричною, якщо вона містить змінну тільки під знаком тригонометричної функції Найпростіші тригонометричні нерівності – це нерівності виду: sinx > a sinx < a cosx > a cosx < a tgx > a tgx < a ctgx > a ctgx < a
у х 0 1.Будуємо одиничне тригонометричне коло 2,Будуємо пряму 3.Знаходимо на од.колі точки,значення ординат яких не менші 1 -1 1 -1 4. 5.Отже, розв'язками нерівності будуть усі значення х з проміжку 6.Враховуючи періодичність функції Відповідь:
у х 0 1.Будуємо одиничне тригонометричне коло. 2,Будуємо лінію тангенсів, пряму 3.відмічаємо на ній точку з ординатою 1. 1 -1 1 -1 4.На промені ТА лежать точки, ординати яких не більші за 1. 5.Отже, розв'язками нерівності будуть усі значення х з проміжку 6.Враховуючи періодичність функції Відповідь: Т(1;1) А
№77 Відповідь:
№72 -1 1 x y Відповідь:2
№71 Знайдемо нулі функції: Нанесемо на одиничне коло область визначення і нулі функції. х у + _ _ Відповідь:6
№76 -2 -1 1 - - -1 -2 1 -1 x y x y
№72 x y Відповідь: 5
про публікацію авторської розробки
Додати розробку