Опорний конспект і тести до теми " Функція"
Лекція 1 «Функція. Властивості функції»
Пригадай !
Що таке функція?
Що таке аргумент функції?
Як можна задати функцію?
Які властивості функцій вивчали раніше?
Функцією називається залежність змінної у від змінної х, якщо кожному значенню змінної х відповідає єдине значення змінної у.
Позначається або f(x), або у = f(x)
х — незалежна змінна, або аргумент.
у - залежна змінна, або значення функції.
у = 2х + 4
Способи задання функції:
|
Спосіб |
Приклад |
||||||||||||||||||||
|
формульний
|
у = - 4х;
у =
у =
у = |
||||||||||||||||||||
|
словесний |
Швидкість авто – 70 км/год. Залежність пройденого шляху s (функція) від часу t(аргумент) можна подати формулою s=70t |
||||||||||||||||||||
|
табличний |
|
||||||||||||||||||||
|
графічний |
|
Що значить дослідити властивості функції?
Це означає виявити її найважливіші властивості:
- вказати область визначення ;
- вказати область значень;
- з`ясувати, чи є дана функція парною або непарною;
- знайти точки перетину з віссю Оу;
- знайти нулі функції та проміжки знакосталості;
- визначити проміжки зростання чи спадання;
- побудувати графік функції.
Основні поняття та властивості функції
|
Поняття / властивість функції |
Позначення |
Означення |
Приклади |
|
Область визначення функції у= f(x) |
D (у) |
всі допустимі значення аргумента. |
1) у = - 3х + 12,
D(у) = (-
2) у =
D(у) = [0;+
3) у =
D(у )= (
4) у =
D(у) = ( |
|
Область значень функції у= f(x) |
Е (у) |
всі значення, яких набуває залежна змінна. |
1)у = - 3х + 12,
Е(у) =(- 2) у = - 4х ,
Е(у) = (-
3) у =
Е(у) = [0;+
4) у =
Е(у) = (
|
|
Графіком функції у= f(x) |
|
множина всіх точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати – відповідним значенням функції |
|
|
Нулі функції |
|
значення аргумента, при яких функція дорівнює нулю. (абсциси точок перетину графіка функції з віссю Ох)
Щоб знайти нулі функції y= f(x), треба розв'язати рівняння f(x) = 0
|
1) у= 2х-6, 2х-6=0, 2х = 6, х=3. 3 - нуль даної функції.
2) у =
х=0 0 - нуль даної функції.
3) у =
так як то функція нулів не має.
|
|
Проміжки знакосталості |
|
проміжки з області визначення функції, на яких дана функція набуває додатних чи від'ємних значень.
Щоб знайти проміжки, на яких функція у = f(x) набуває додатних значень, треба розв'язати нерівність f(x) > 0, від'ємних - f(x) < 0.
|
1)у = 6х -12 у >О: 6х-12>О, 6х >12;
х > 2; При х є (2; + 6х<12; х<2.
При х є (-
2) у =
Оскільки
при х є [0;
то у > 0 при є (0;+
|
|
Функція y=f(x) зростає на проміжку [а;в]
|
|
якщо більшому значенню аргументу х з цього проміжка відповідає більше значення функції у, а меншому х - менше у. Тобто, якщо х1 > х2 (х1 є [а; в], х2 є [а;в]) і f(x1 ) > f(x2 ), то f(x -зростає на[а;в].
Якщо функція зростає на всій області визначення, то вона називається зростаючою.
|
При х є [0;+
При k > 0 зростає для х є D(y). Отже, це зростаюча функція.
При к < 0 дана функція зростаюча.
|
|
Функція y = f(x) спадає на проміжку [а;в] |
|
якщо більшому значенню аргумента х з цього проміжка відповідає менше значення функції у, а меншому х - більше у. Тобто, якщо х1> х2 (х1 є [а;в], х2 є [а;в]) і f (х1) < f(x2), то f(x) - спадає на[а;в].
Якщо функція спадає на всій області визначення, то вона називається спадною.
|
При х є (-
При k < 0 спадає для х є D(y), то це спадна функція.
При k > 0 дана функція спадна.
|
|
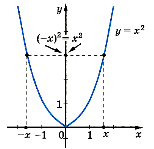
Функція у = f (х) - парна |
|
якщо її область визначення симетрична відносно нуля і для кожного х з області визначення f (-х) = f(x).
Графік парної функції симетричний відносно осі Оу |
у = х2
D(y) = (- Оскільки у(- х) = (- х )2 = х2 = у(х), то у = х2 – парна функція.
|
|
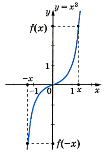
Функція у = f(x) - непарна |
|
якщо її область визначення симетрична відносно нуля і для кожного х з області визначення f(-x) = - f(x).
Графік непарної функції симетричний відносно початку координат.
|
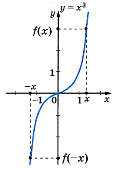
у = х3.
D(y) = (- Оскільки у(-х)=(-х) 3 = -х3 = - у(х), то у = х3 – непарна функція.
|
|
Функція у = f(x) –ні парна, ні непарна |
|
або якщо її область визначення несиметрична відносно нуля , або для кожного х з області визначення
f (-х)
і f (-х)
Графік ні парної ні непарної функції несиметричний відносно початку координат та осі Оу
|
у = ( х-3)2
D(y) = (- Оскільки
у(- х) = (- х-3 )2 = х2+6х+9 то у = х2 – ні парна , ні непарна функція.
|
Дослідивши властивості функції, можна побудувати графік функції за отриманими точками.
Тест 1 «Функція та її властивості»
- Функція задана формулою у= х3-х2+1 . Обчислити у(-1)
- 3
- 1
- -1
- -3
- Які з точок належить графіку функції у= 3х-1
- (-3;-8)
- (-1;-4)
- (0;-1)
- (-2;5)
-
Область визначення функції у=
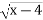
- (-4;∞)
- [-4;∞)
- (4;∞)
- [4;∞)
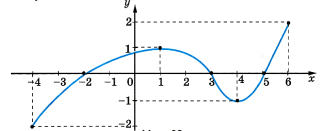
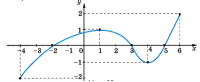
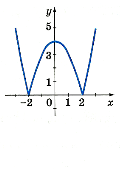
- Областю значень функції, зображеної на рисунку є проміжок:
-
 (-4;-6)
(-4;-6)
- (-1;2)
- (0;6)
- (-2;2)
-
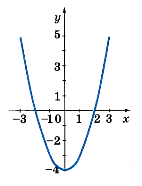
Нулі функції У=
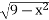
- 3
- -3 і 3
- -3
- 9
-
Задано функцію у=
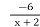 . Яке з тверджень правильне:
. Яке з тверджень правильне:
- у(0) = -3
- Областю визначення функції є всі дійсні числа.
- Графік функції проходить через точку А(-8;6)
- Область визначення функції задається умовою х≠-2
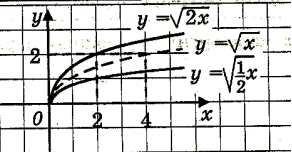
- Областю визначення якої з функцій є множина дійсних чисел
-
у=
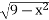
-
у=
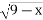
-
у=
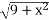
-
у=
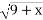
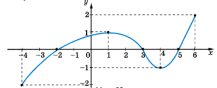
- Вказати проміжок спадання функції , графік якої зображений на рисунку:

- (-4;1)
- [1;4]
- [-4;∞)
- (1;6)
- Встановити відповідність між твердженням і графіком функції
Функція парна –
Функція непарна –
Функція ні парна, ні непарна –
-
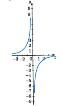
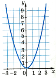
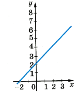 b) c)
b) c)
- За графіком функції f(x), зображеному на рисунку, визначити неправильне твердження:
-
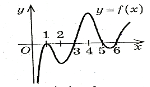 Якщо х є (1;3), то f(x ) < 0
Якщо х є (1;3), то f(x ) < 0
- Якщо х є [3;5], то f(x) ≥ 0
- f(x) > 0,якщо х є (3;5), х є (6;∞)
- Якщо х є (5;6), то f(x) > 0
- Нулі функції: 1, 3, 5, 6
- Функція у= 1,5х – 2 задана на проміжку [-2;5]. Знайти найбільше значення функції
- -5
- -2
- 5,5
- 9,5
-
Визначити область значень функції у =
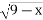
-
(-
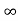 ;+
;+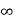 );
);
-
(
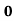 ;+
;+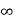 );
);
-
(-
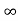 ; 0 );
; 0 );
-
 [ 0 ;+
[ 0 ;+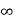 );
);
Відповіді до тесту 1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
c |
b, c |
d |
d |
b |
a, d |
c |
b |
b, c, a |
d |
с |
d |
в |
Лекція 2 «Приклади функцій та їх властивості»
Пригадай !
Як дослідити властивості та побудувати графік функції?
Що таке графік функції?
Що таке область визначення функції?
Що таке область значень функції?
Властивості яких функцій вивчали раніше?
|
№ |
Назва |
формула |
Властивості функції |
Графік |
|
1 |
лінійна |
у= k x + l |
D(у) = (-
Е(у) =(- Функція ні парна ні непарна Проходить через точку ( 0; l )
Нулі функції: х=
Якщо
При х є (
При х є ( Функція зростаюча
Якщо
При х є (
При х є ( Функція спадаюча |
Графік – пряма
у= x + 2
2)
|
|
2 |
Пряма пропорційність (лінійна, l = 0) |
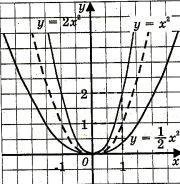
у= k x |
D(у) = (-
Е(у) =(- Функція непарна Проходить через початок відліку
Якщо
При х є (
При х є ( Функція зростаюча
Якщо
При х є (
При х є ( Функція спадаюча |
Графік – пряма, яка проходить через початок відліку у=2х
|
|
3 |
Стала |
у = k |
D(у) = (-
Е(у) = Функція парна
Графік проходить через точку (0;k), не перетинає вісь Ох
|
Графік – пряма, паралельна осі Ох у = 3,5
|
|
4 |
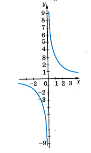
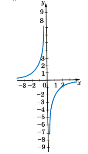
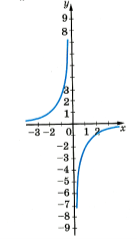
Обернена пропорційність |
у = |
D(у) = (-
Е(у) =(- Функція непарна Графік не перетинає вісі Ох, Оу
Якщо
При х є (
При х є (
Функція спадаюча
Якщо
При х є (
При х є (
Функція зростаюча |
Графік – гіпербола
|
|
5 |
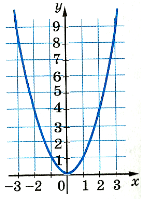
Квадратична |
у = x2 |
D(у) = (-
Е(у) = Функція парна Проходить через початок відліку
При х є (
При х є
|
Графік – парабола з двома вітками, направленими вгору
|
|
6 |
|
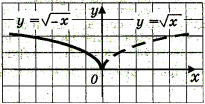
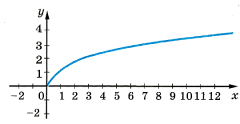
у= |
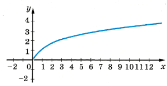
D(у) = [
Е(у) = [ 0;+ Функція ні парна ні непарна Проходить через початок відліку
Функція зростаюча
|
Графік – парабола з однією віткою
|
|
7 |
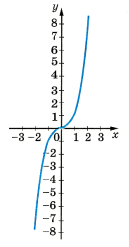
Кубічна |
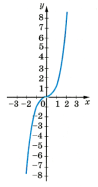
у = x3 |
D(у) = (-
Е(у) =(- Функція непарна Проходить через початок відліку
При х є (
При х є (
Функція зростаюча
|
Графік – парабола з двома вітками, направленими вгору та вниз
|
Тест 2 «Приклади функцій та їх властивості»
- Графік якої функції проходить через початок координат
- у= х2
-
у=
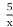
- у= -3х+4
-
у=
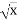
- Графіком якої з наведених функцій є горизонтальна пряма
-
у=
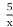
- у=х2
- у= -3
- у= -3х+4
- Графіком якої з поданих функцій є парабола з однією віткою
- у=х2
-
у=
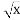
- у= -3х+4
-
у=
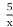
- На якому з рисунків зображений графік оберненої пропорційності:
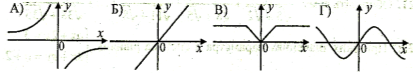
- Яка з лінійних функцій є спадна і не проходить через початок відліку:
- у= х
-
у=
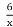
- у= 4-3х
- у=2х+5
- Яка з наведених прямих перетинає пряму у = -3х+7
- у = -3х+7
- у = 3х+7
- у = -3х-1
- у = -3х
- Які з функцій спадні на множині дійсних чисел
- у= -х3
-
у=
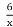
- у = х2
- у= -5х+1
- Для яких функцій область визначення є множина всіх дійсних чисел
- у= х2+5
-
у=
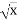
- у=2х+5
-
у=
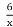
- Для кожної функції вказати відповідний графік
у= ![]()
у= х2
у= 3,5
у=![]()
a)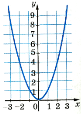 b)
b)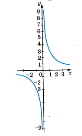 c)
c) 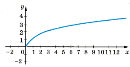 d)
d) 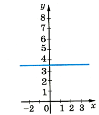
- Графік якої з функцій не перетинає вісь Ох
-
у=
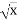
-
у=
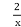
- у= 2х
- у= х2
Відповіді до тесту 2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
а, d |
c |
b |
a |
c |
b |
a, d |
a, c |
c, a, d, b |
b |
Лекція 3 « Найпростіші перетворення графіків функцій»
|
№ |
Функція |
перетворення графіка |
Зразок |
|
1 |
у = - f (x) |
Графік функції у = f(x) відобразити симетрично відносно осі Ох.
|
|
|
2 |
у = f ( - x) |
Графік функції у = f(x) відобразити симетрично відносно осі Оу.
|
|
|
3 |
у = f ( x |
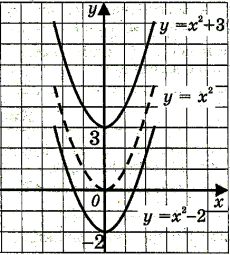
Виконати паралельне перенесення графіка функції у = f(x) вздовж осі Оу
на а одиниць вгору, якщо а > 0 на -а одиниць вниз, якщо а < 0.
|
|
|
4 |
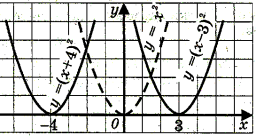
у = f ( x |
Виконати паралельне перенесення графіка функції у = f(x) вздовж осі Ох
на а одиниць вправо, якщо а < 0. на а одиниць вліво, якщо а > 0
|
|
|
5 |
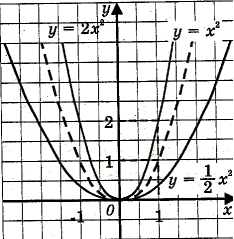
у = k f ( x ) k >0 |
Графік функції у = f ( x)
якщо k >1 розтягти від осі Ох у k разів
якщо 0< k < 1
стиснути в
|
|
|
6 |
у = f ( k x ) |
Графік функції у = f ( x)
якщо k >1 стиснути вздовж осі Ох у k разів
якщо 0< k < 1
розтягти вздовж осі Ох в
|
|
|
7 |
у = |
у =
Побудувати графік функції
|
|
|
8 |
у =f( |
Так як f ( то функція парна, а тому графік функції симетричний відносно осі Оу
Побудувати графік функції
|
|
Тест 3 «Найпростіші перетворення графіків функцій»
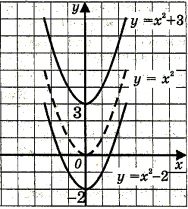
- Графік функції у= - х2 перенесли на 3 одиниці вгору вздовж осі ординат. Графік якої функції було отримано?
- у= - (х+3)2
- у= - (х-3)2
- у= -х2- 3
- у= -х2 + 3
-
Графік функції у=
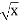 перенесли паралельно на 2 одиниці вліво вздовж осі абсцис. Графік якої функції було отримано?
перенесли паралельно на 2 одиниці вліво вздовж осі абсцис. Графік якої функції було отримано?
-
у=
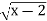
-
у=
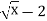
-
у=

-
у=
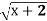
- На якому з рисунків зображено графік функції у= (х - 4)2
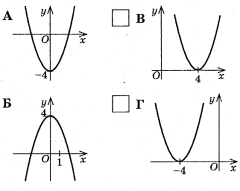
- Дано параболу у= х2. Рівняння параболи, яку можна отримати з даної перенесенням на 2 одиниці праворуч і з одиниці вгору:
- у= (х-2)2+3;
- у= (х+2)2-3;
- у= (х-3)2+2;
- у= (х+3)2-2;
-
Як треба перенести паралельно графік функції у =
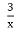 , щоб отримати графік функції у=
, щоб отримати графік функції у=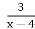
- на 4 одиниці вгору
- на 4 одиниці вправо
- на 4 одиниці вниз
- на 4 одиниці вліво
- Вказати квадратичну функцію, графік якої зображений на малюнку:
-
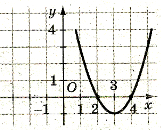 у= (х-3)2+1;
у= (х-3)2+1;
- у= (х+3)2-1;
- у= (х-3)2-1;
- у= (х+3)2+1;
-
Вказати рисунок на якому зображений графік функції у=
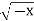
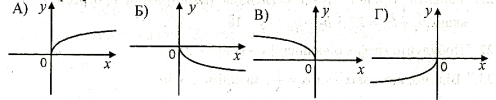
- Встановити відповідність між функціями та графіками
 у= - х-2
у= - х-2
у= х-2
у= х+2
у= - х+2
Відповіді до тесту 3
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
d |
d |
в |
a |
b |
c |
в |
Б,г, а, в |
|
|
Тест 4 «Квадратична функція»
- Яка з функцій є квадратичною:
- у= -3х+2;
- у= -4х2-3х+2;
- у= 4х3-3х+2;
-
у=
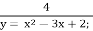
- Графіком квадратичної функції є
- гіпербола,
- парабола з однією віткою;
- пряма;
- парабола з двома вітками
- Чому дорівнює абсциса вершини параболи у= -2х2+12х
- 3
- 6
- -6
- -3
- Вершина якої з парабол належить осі ординат:
- у= х2 +4;
- у= х2 +5х -4;
- у= х2 -4х+4;
- у= х2 +5х
- Вершина якої з парабол належить осі абсцис:
- у= х2 +4;
- у= (х+4)2;
- у= х2 +4;
- у= (х-2 )2 - 1;
- У якій координатній чверті знаходиться вершина параболи у= (х-2 )2 - 6;
- у І чверті
- у ІІ чверті
- у ІІІ чверті
- у ІV чверті
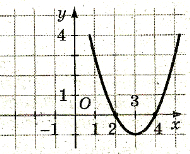
- На рисунку зображений графік функції у= х2 +4х+3. Вказати найменше значення функції.
- -1
- -3
- -2
- 0
- Чому дорівнюють абсциси точок перетину параболи у= х2 -4х-21 з віссю абсцис?
- 6;-2
- -7;3
- -6; 2
- 7; -3

- Користуючись рисунком, вказати проміжок, на якому функція недодання
- [2;4]
-
(-∞;2]
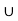 [4; ∞)
[4; ∞)
- (2;4)
-
(-∞;2)
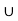 (4; ∞)
(4; ∞)
-
 Користуючись рисунком, вказати проміжок, на якому функція спадає
Користуючись рисунком, вказати проміжок, на якому функція спадає
- [2;4]
-
(-∞;2]
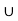 [4; ∞)
[4; ∞)
- (-∞;3]
- (3; ∞)
- Яка з даних функцій є зростаючою на проміжку [0; ∞)?
- у= -х2 +4;
- у= (х-4)2;
- у= х2 +4;
- у= -х2 -1
- Які з тверджень вірні?
- Графік функції у= х2 +4х є парабола, вітки якої направлені вниз.
- (0; 3)- координати вершини параболи, що є графіком функції у= -х2 +3;
- Вершини параболи, що є графіком функції у= (х+3)2, належить осі ординат
- Графік функції у= х2 -9х-7 є парабола, вітки якої направлені вгору
- На рисунку зображений графік функції у= х2 +3х+2. Які з тверджень невірне?
- -2 і -1 - нулі функції
- у≤ 0, якщо х є [ -2; -1]
- у зростає , якщо х є (- ∞;-1,5)
- -1,5 – найменше значення функції
- Встановити відповідність між заданими функціями та графіками:
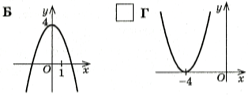
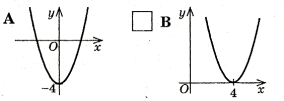 у= х2 - 4;
у= х2 - 4;
у= - х2+ 4
у= (х +4) 2
у = (х -4) 2
- Встановити відповідність за графіком функції
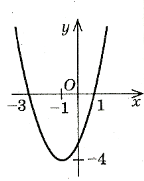 D(у)
D(у)![]()
Е(у)![]()
у![]()
координати вершини параболи
- [ -4; ∞)
- (-1; -4)
- (-∞; ∞)
- (-3; 1)
Відповіді до тесту 4
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
b |
d |
a |
a |
b |
d |
a |
d |
а |
с |
c |
b, d |
c, d |
a,b,г,в |
c,a,d,b |

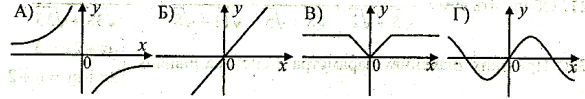


про публікацію авторської розробки
Додати розробку