Опорний конспект "Квадратні рівняння. Неповні квадратні рівняння"

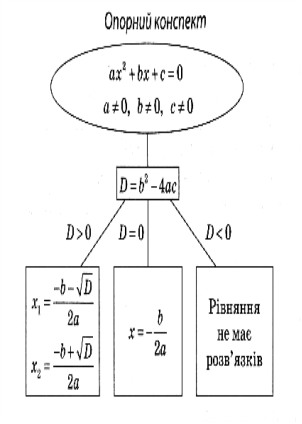
Формула коренів квадратного рівняння

                                                                                 (1)

  Оскільки  ,  то,   помноживши обидві частини цього рівняння на  4а,  отримаємо рівняння,  рівносильне даному:

      .

  Виділимо в лівій частині цього рівняння квадрат двочлена:

    ;

     ;

                                              .                              (2)

  Існування коренів цього рівняння та їхня кількість залежать від знака значення виразу .  

  -   дискримінант  квадратного  рівняння .

(увів термін англійський математик Джеймс Сільвестр)

   Отже, рівняння  (2)  можна записати так:   .         

   Можливі три випадки:    D < 0,    D = 0,    D > 0 .

• Квадратне рівняння, перший коефіцієнт якого дорівнює 1, називають  зведеним.

           Наприклад,  ,     ,       –  це зведені  квадратні  рівняння.  

• Оскільки , то незведене квадратне рівняння завжди можна перетворити  у  зведене,  рівносильне  даному.

Розділивши  обидві  частини  рівняння  на число а,  отримаємо  зведене  квадратне  рівняння  .

• Якщо у квадратному рівнянні хоча б один із коефіцієнтів  b або с  дорівнює нулю, то таке рівняння називають  неповним  квадратним  рівнянням.

• Існує  три  види  неповних  квадратних  рівнянь:

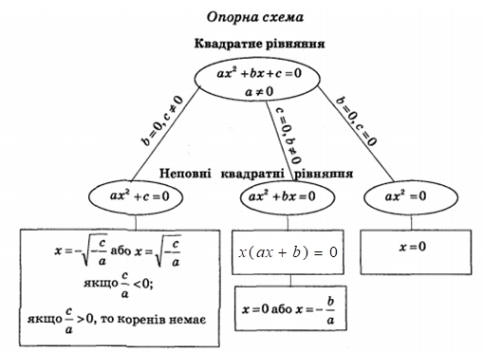
1)  при  b = с = 0   маємо:  ;

2)  при  с = 0   і     маємо:  ;

3)  при  b = 0   і     маємо:  .

Квадратні рівняння.  Неповні квадратні рівняння

• Рівняння  виду ,   де  х – змінна,   а і b – деякі числа, називають  лінійними  рівняннями.
• Якщо ,  то рівняння називають рівнянням першого степеня.

Наприклад,  ,    ,      є  рівняннями першого степеня.

• Числа  а і b  називають  коефіцієнтами рівняння першого степеня  .

• Квадратним  рівнянням   називають  рівняння  виду ,  де х – змінна,   а, b і с – деякі числа,  причому .
•  Числа  а, b і с називають коефіцієнтами квадратного рівняння:

  число а  називають  першим (або старшим) коефіцієнтом,

  число b  називають  другим  коефіцієнтом,

  число с  називають  вільним членом.

 Наприклад,    має  такі  коефіцієнти: 

а = ___,     b = ___,     с = ___ .

№ 592

Складіть квадратне рівняння,  у якому:

1. старший коефіцієнт дорівнює 6,  другий коефіцієнт дорівнює 7, а  вільний  член  дорівнює  2.

Розв’язання:  __________________.

2. старший коефіцієнт дорівнює 1,  другий коефіцієнт дорівнює –8, а  вільний  член  дорівнює  .

Розв’язання:  __________________,  отже,  __________________.

3. старший коефіцієнт дорівнює 7,2,   другий коефіцієнт дорівнює –2,   а  вільний  член  дорівнює  0.

Розв’язання:  __________________,  отже,  __________________.

Приклади:

1.  Розв’яжіть рівняння  .

Розв’язання:

     ________________________

           ________________________

                      ________________________

                  Відповідь: ___________

2.  Розв’яжіть рівняння  .

Розв’язання:

     ________________________

           ________________________

                      ________________________

                  Відповідь: ___________