Опорний конспект "ПІРАМІДА, ВПИСАНА У КОНУС. ПІРАМІДА, ОПИСАНА НАВКОЛО КОНУСА"
Опорний конспект містить стислий виклад теоретичного матеріалу та приклади розв'язування задач. Формат зручний для роздруковування. Друкувати рекомендую з двох боків аркуша. В результаті з одного аркуша паперу вийде дві картки. Зауваження: функція попереднього перегляду не відображає структуру документа.
Піраміда, вписана у конус
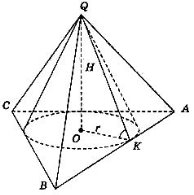
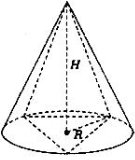
Піраміду називають вписаною у конус, якщо її основа вписана в основу конуса, а вершиною є вершина конуса.
При цьому конус називають описаним навколо піраміди.
Бічні ребра піраміди, вписаної у конус, є твірними конуса.
Властивості піраміди, вписаної у конус
- Конус можна описати навколо піраміди, якщо її основою є многокутник, навколо якого можна описати коло, а висота піраміди проходить через центр цього кола.
- Радіус основи конуса дорівнює радіусу кола R, описаного навколо основи піраміди, а висота конуса Н дорівнює висоті піраміди.
Задача
Навколо піраміди, сторони основи якої дорівнюють 10 см, 10 см і 12 см, а висота 8 см, описано конус. Знайти площу осьового перерізу конуса.
Розв’язання
-
Нехай радіус основи дорівнює R, а висота ‒ Н. Тоді площа осьового перерізу конуса
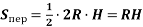 .
.
- Висота конуса дорівнює висоті піраміди, тому Н = 8 см.
-
Радіус конуса знайдемо як радіус кола, описаного навколо трикутника зі сторонами 10 см, 10 см і 12 см. Використаємо формулу
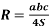 , де а, b, с ‒ сторони трикутника, S ‒ його площа.
, де а, b, с ‒ сторони трикутника, S ‒ його площа.
-
За формулою Герона
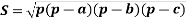 , де
, де 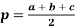 .
.
-
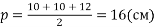 ;
; 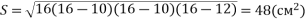 .
.
-
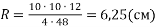 .
.
-
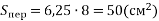 .
.
Піраміда, описана навколо конуса
Піраміду називають описаною навколо конуса, якщо її основа описана навколо основи конуса, а вершиною є вершина конуса.
При цьому конус називають вписаним у піраміду.
Бічні грані піраміди належать площинам, дотичним до конуса.
Площину називають дотичною до конуса, якщо вона проходить через твірну конуса і перпендикулярна до площини осьового перерізу, який містить цю твірну.
Властивості піраміди, описаної навколо конуса
- Конус можна вписати в піраміду, якщо її основою є многокутник, в який можна вписати коло, а висота піраміди проходить через центр цього кола.
- Радіус основи конуса дорівнює радіусу кола r, вписаного в основу піраміди, а висота конуса Н дорівнює висоті піраміди.
Задача
В основі піраміди лежить прямокутний трикутник з катетами 6 см і 8 см, а двогранні кути при основі піраміди дорівнюють по 60º. Знайти висоту конуса, вписаного у піраміду.
Розв’язання
- Нехай у трикутну піраміду з основою АВС і вершиною Q вписано конус. Основа висоти конуса точка О ‒ центр кола, вписаного в ∆АВС.
- Нехай точка К ‒ точка дотику кола, вписаного в ∆АВС, до сторони АВ. Позначимо ОК = r - радіус кола, вписаного в ∆АВС, а також радіус основи конуса.
-
ОК
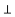 АВ, за теоремою про три перпендикуляри QК
АВ, за теоремою про три перпендикуляри QК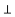 АВ, тому
АВ, тому 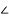 QКО ‒ лінійний кут двогранного кута при ребрі основи піраміди. За умовою
QКО ‒ лінійний кут двогранного кута при ребрі основи піраміди. За умовою 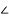 QКО = 60°.
QКО = 60°.
-
Радіус кола, вписаного у прямокутний трикутник, знайдемо за формулою
 , де а, b ‒ катети, с ‒ гіпотенуза.
, де а, b ‒ катети, с ‒ гіпотенуза.
-
За умовою АС = 6 см, ВС = 8 см ‒ катети. Тоді гіпотенуза
 АВ = 10 см. (∆АВС ‒ єгипетський).
АВ = 10 см. (∆АВС ‒ єгипетський).
-
OK =
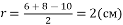 .
.
-
QO ‒ висота піраміди і конуса. З ∆OQK (
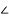 O=90°):
O=90°): 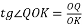 , тоді
, тоді 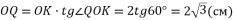 .
.


про публікацію авторської розробки
Додати розробку
