«Основні види рівнянь з однією змінною. Методи їх розв’язання.»


![Готуємось до ЗНОАБВГДR(-∞; -1][5; +∞)(-1; 5)[-1; 5] 1. Знайти область визначення ( область допустимих значень ) рівняння 2. Яке з наведених рівнянь має корені?АБВГД3. Знайти суму коренів рівняння АБВГД9-93-32 Готуємось до ЗНОАБВГДR(-∞; -1][5; +∞)(-1; 5)[-1; 5] 1. Знайти область визначення ( область допустимих значень ) рівняння 2. Яке з наведених рівнянь має корені?АБВГД3. Знайти суму коренів рівняння АБВГД9-93-32](/uploads/files/633777/231799/247711_images/3.jpg)


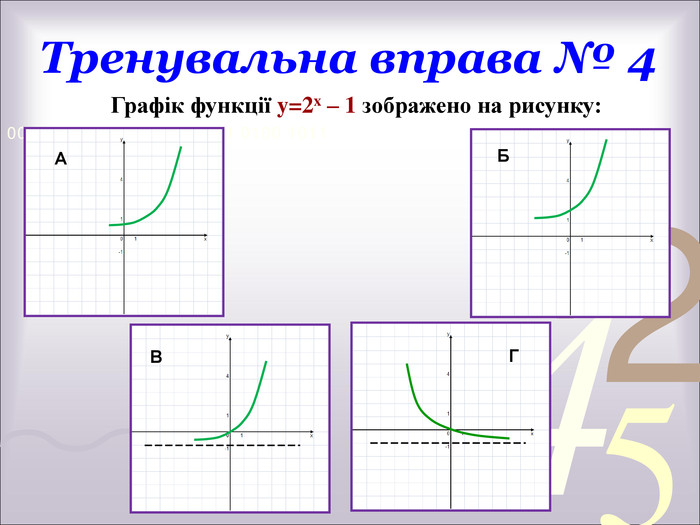

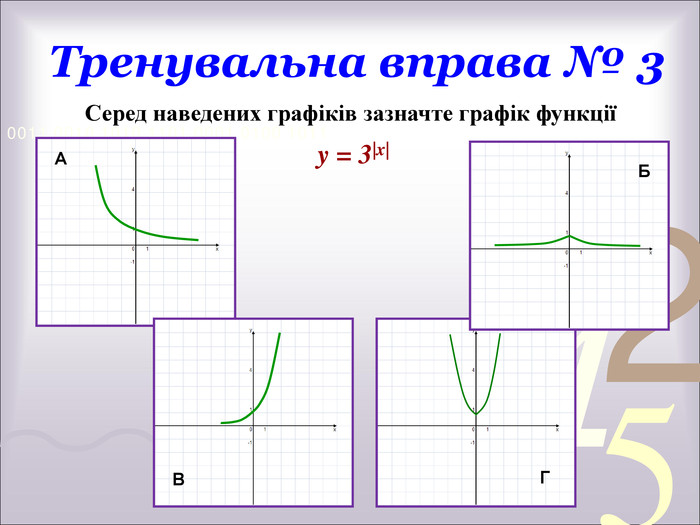











![Тест.1. Обчислити: а) 4; б) 2; в) 0,5; г) 82. Обчислити: а) -2; б) - 6; в) 34; г) розв’язку немає3. При яких значеннях х вираз має зміст: а)[0;∞) ; б)(- ∞; 5] ; в) ( - ∞; +∞) ; г) [5; +∞)4. Розв’язати рівняння: а) 4; б) 2; в) 16; г) -25. Розв’язати рівняння: а) 11; б) 21; в) -16; г) 1216. Розв’язати рівняння: а) 2; б) 265; в) -265; г) коренів немає7. Розв’язати рівняння: а) 1; -3,5; б) 1; 3,5; в) -1; г) -1; -3,5. Тест.1. Обчислити: а) 4; б) 2; в) 0,5; г) 82. Обчислити: а) -2; б) - 6; в) 34; г) розв’язку немає3. При яких значеннях х вираз має зміст: а)[0;∞) ; б)(- ∞; 5] ; в) ( - ∞; +∞) ; г) [5; +∞)4. Розв’язати рівняння: а) 4; б) 2; в) 16; г) -25. Розв’язати рівняння: а) 11; б) 21; в) -16; г) 1216. Розв’язати рівняння: а) 2; б) 265; в) -265; г) коренів немає7. Розв’язати рівняння: а) 1; -3,5; б) 1; 3,5; в) -1; г) -1; -3,5.](/uploads/files/633777/231799/247711_images/20.jpg)





































Розв'язання лінійного рівняння ах=в.1. Якщо а ≠ 0, то рівняння має один корінь. Наприклад, 3,4х-6,8=0, х=6,8:3,4, х=2. Відповідь:22. Якщо a=0, але b ≠ 0, то рівняння немає коренів. Наприклад, 4·(3х-1)=12х+10, 12х-4=12х+10, 12х-12х=10+4, 0·х=14немає такого значення x, при множенні якого на 0 можна отримати 14,тому дане рівняння розв´язків немає. Відповідь: ∅3. Якщо a=0 і b=0, то корінь рівняння — будь-яке число. Наприклад, 3,8·(х-1)=5,7х-1,9·(х+2), 3,8х-3,8=5,7х-1,9х-3,8, 3,8х-3,8х=-3,8+3,8, 0·х=0нуль при множенні на будь-яке число, дає 0,тому розв´язком даного рівняння є будь-яке число. Відповідь:х∈(−∞;+∞) Це трба вміти. Це треба знати
Розв'язок пропорцій.1. Розв´язати рівняння: 𝟏х−𝟏 = 𝟐х+𝟏. Для розв´язування використовуємо основну властивість пропорції 1·(х+1)=2·(х-1), х+1= 2х-2, х-2х = -2-1, х=3. Відповідь:32. Розв´язати рівняння: х+𝟓𝟏𝟎(х−𝟓) = 𝟏х−𝟓,(х+5)(х-5)=10х-50,х²-25-10х+50=0,х²-10х+25=0,(х-5)²=0,Х=5. При х=5 знаменики дробів,що входять до даного рівняння дорівнюють нулю.тому це значення х не може бути коренем рівняння. Відповідь: рівняння розв´язків не має. Це треба вміти
Квадратні рівняння. Рівняння виду ax²+bx+c=0, де a, b і c — дійсні числа та a≠0, називається квадратним рівнянням. Сума коренів зведеного квадратного рівняння х²+px+g=0 дорівнює взятому з протилежним знаком другому коефіцієнту, а добуток–вільному члену(Теорема Віета ): x1 +x2 = -p; x1· x2 =g. Наприклад: х²- 5х + 6=0, p=-5, g=6. x1 +x2 =5; x1· x2 =6. Корені знаходимо методом підбору. Відповідь:2;3. Це треба знати
Приклади. Біквадратним називається рівняння виду a𝒙𝟒+bx²+c=0 де x – змінна, a, b, c– деякі числа,причому a≠𝟎 . 1. Розв´язати рівняння: х𝟒+5х²+4=0,Робимо заміну змінної: х²=t, х𝟒= t²Розв´язуємо отримане квадратне рівняння відносно t. t²+5 t+4=0,Розв´язавши дане рівняння або за формулою коренів, або за теоремою Вієта отримаємо t=-1; t=-4. Робимо обернену заміну:1) х²=-1 –рівняння розв´язків не має.2) х²=-4 - рівняння розв´язків не має. Відповідь :рівняння розв´язків не має.2. Розв´язати рівняння: х𝟒−5х²+4=0,Робимо заміну змінної: х²=t, х𝟒= t²Розв´язуємо отримане квадратне рівняння відноно t. t²-5 t+4=0 Розв´язавши дане рівняння або за формулою коренів, або за теоремою Вієта отримаємо t=1; t=4. Робимо обернену заміну:1) х²=1; х=-1,х=12) х²=4; х=-2,х=2. Відповідь:-2;-1;1;2. Це треба вміти
Дробово-раціональні рівняння. Дробово- раціональне рівняння — це рівняння, в якого ліва або права частина або обидві — дробові вирази. Це треба знати1. Розв´язати рівняння:х+𝟏х+𝟐−(х−𝟐)(х−𝟑)(х−𝟐)(х+𝟐)=0,𝟖х−𝟒х²−𝟒=0, 8х-4=0 ,х=0,5. При х=0,5 знаменник х²−𝟒≠𝟎, отже х=0,5-корінь рівняння.2. Розв´язати рівняння:х𝟑−𝟗хх𝟑+𝟐𝟕=0, х(х−𝟑)(х+𝟑)(х+𝟑)(х𝟐−𝟑х+𝟗)=𝟎, х(х−𝟑)(х+𝟑)=0, х1=0;х2=3;х3=-3 . При х=-3 знаменник дорівнює 0,отже число -3 даного рівняння не задовільняє. Відповідь:0; 3.
Приклад1. Розв´язати рівняння:х−5+4−х= 7,Знайдемо ОДЗ:х−5≥0, 4−х≥0. х≥5,х≤4 Як бачимо система розв´язків не має, тому, рівняння також не має розв'язків, бо нема загальних значень х, для яких обидва радикали мають дійсне значення.2. Розв´язати рівняння: 𝟓х =1,х=15, ,(х)²= (15)², х= 125.3. Укажіть якому проміжку належить корінь рівняння: 13−5х=3, ( 13−5х)²=3², 13-5х=9, 5х=4, х=0,8 ,х∈(0;1) х45 Це треба вміти
Приклад(ПЗНО 2020)4. Розв´язати рівняння:х³=-0,027,добуваємо з лівої і правої частини𝟑х³𝟑х³ = 𝟑−𝟎,𝟎𝟐𝟕𝟑х³ = 𝟑(−𝟎,𝟑)³Х=-0,35. Розв´язати рівняння: х - х -2 = 0, х-2= х, ( х-2)²= (х)², х²-4х+4-х=0, х²-5х+4=0, х1=1; х2=4. Перевірка: , х1=1, 1-𝟏 -2=0 -2 ≠𝟎-сторонній корінь. х2=4, 4-𝟒 -2=4-2-2=0. 0=0 Відповідь;х=4. Це треба вміти
Тест.1. Обчислити: а) 4; б) 2; в) 0,5; г) 82. Обчислити: а) -2; б) - 6; в) 34; г) розв’язку немає3. При яких значеннях х вираз має зміст: а)[0;∞) ; б)(- ∞; 5] ; в) ( - ∞; +∞) ; г) [5; +∞)4. Розв’язати рівняння: а) 4; б) 2; в) 16; г) -25. Розв’язати рівняння: а) 11; б) 21; в) -16; г) 1216. Розв’язати рівняння: а) 2; б) 265; в) -265; г) коренів немає7. Розв’язати рівняння: а) 1; -3,5; б) 1; 3,5; в) -1; г) -1; -3,5.
Рівняння, що містять змінну під знаком модуля. Суть розв’язання рівнянь з модулями полягає в тому, щоб звільнитися від модулів(або за означенням модуля або методом інтервалів) і перейти до рівнянь, які не містять модулів, і розв’язувати вже відомим способом. Кількість коренів рівняння |f(x)| = a в залежності від значення числа a:1.а < 0-рівняння коренів не має.2.а=0-рівняння має один корінь.3.а˃0-рівняння має два корені:𝑓𝑥=𝑎,𝑓𝑥=−𝑎 Це треба знати
Приклади1. Розв´язати рівняння: 𝟑х−𝟕=8 Модуль числа дорівнює 8 тоді і лише тоді, коли це число дорівнює 8 або – 8. Отже:3х-7=8 або 3х-7= -83х=15 , 3х= -1, х=5 х= -13. Відповідь: -13;5.2. Розв´язати рівняння:𝟒х−𝟏−𝟓=7,4х−1-5=7, або 4х−1-5=-74х−1=12, 4х−1 = -2-розв´зків немає..4х-1=12 або 4х-1=-124х=13 4х=-11. Х=3,25 х=-2,75 Відповідь:-2,75; 3,25. Це треба вміти
Система двох рівнянь𝟐х+у=𝟒,𝟑х+𝟓у=𝟏𝟑; Розв´яжемо дану систему способом підстановки, для цього виразимо з першого рівняння змінну у через х: у=4-2х і підставимо у друге рівняння замість у:3х + 5·(4-2х) = 13,3х+20-10х=13,3х-10х=13-20,-7х=-7,Х=1. Підставивши знайдене значення х у вираз у=4-2х,знайдемо значення у. у=4-2·1=2. Відповідь:(1;2). Це треба вміти
Приклади (ЗНО)1. Розв´яжіть систему рівнянь. Оскільки коефіцієнти при змінній у протилежні, то дану систему зручно розв´язати способом додавання. Додавши почленно перше і друге рівняння отримаємо: 3х=3, х=1. Підставимо отримане значення у будь-яке із рівнянь 1+3у = -11,3у = -12,У = -4. Відповідь:(1;-4)2. Скільки розв´язків має система рівнянь:х²−у𝟐=−𝟓,х²+у𝟐=𝟒.2х² = -1, х² = - 0,5 -система розв´язків не має оскільки х² ≥ 0, а-0,5<0. 𝟐х−𝟑у=𝟏𝟒,х+𝟑у=−𝟏𝟏 +Це треба вміти
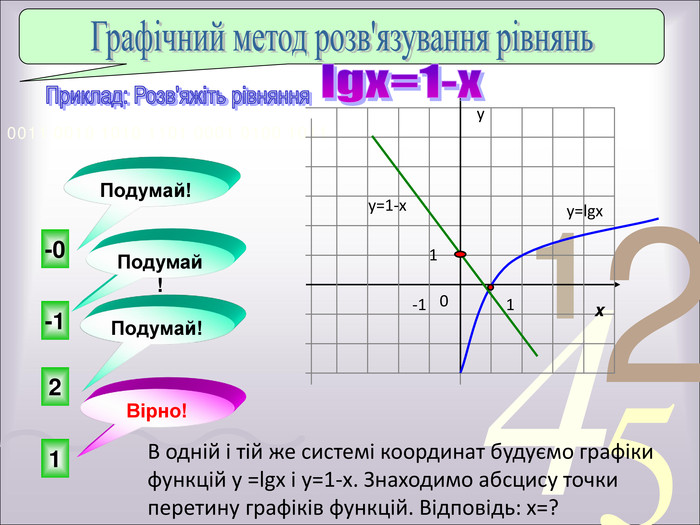
Графічний спосіб3. Графічний спосіб :будуємо в одній системі координат графіки обох рівнянь системи.знаходимо координати спільних точок графіків.координати цих спільних точок і є розв'язками системи. Розв´язати графічно систему рівнянь:2х−у=2,х+у=4.1)Будуємо графік рівняння 2х-у=2,у=2х-22)Будуємо графік рівняння х+у=4,у=4-х3) За отриманими даними будуємо в одній системі координат графіки обох рівнянь системи4)Графіки перетинаються в точці (2;2)Відповідь:(2;2) {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}х01у-20{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}х04у40 Це треба знати. Це треба вміти


про публікацію авторської розробки
Додати розробку


























































-

Паншина Наталія Миколаївна
14.11.2024 в 13:21
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Жуковська Валентина
30.01.2024 в 19:10
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Жуковська Валентина Василівна
04.02.2023 в 23:05
Дякую за змістовний матеріал!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сологуб Ольга Юріївна
20.12.2022 в 18:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сологуб Ольга Юріївна
20.12.2022 в 18:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука