Освітній сценарій з геометрії Узагальнення та систематизація знань з теми"Розв'язування трикутників"

Освітній сценарій з геометрії за темою:

 Узагальнення та систематизація знань з теми  «Роз’язування трикутників»

Вчитель ЯКОВИШИНА Н.В.

Основні задачі психологічно- соціального розв’язку:

•    елементи логічного та абстрактного мислення;
•    комунікативність;
•    вміння працювати самостійно.

Результати навчального модуля:

Знати:

• теореми синусів та косинусів та наслідки з них;
• співвідношення між кутами трикутника та протилежними сторонами;
• формули для знаходження площі трикутника. 

Нормувати:

• вміння застосовувати теореми косинусів та синусів при розв’язуванні задач;
• вміння знаходити площу трикутника;
• вміння розпізнавати проблему, стисло та зрозуміло формулювати власну думку.

Цінувати:

• вміння  відтворювати зміст вивчених понять;
• відповідальність, працьовитість, уважність.

І міні-модуль

Локалізація пізнавальної проблемності

Цільова установка на активний пошук учнями нових наукових знань.

ІІ міні-модуль

Адаптація теоретичних знань.

Розширення ментального досвіду

Застосовування наукового знання

на практиці

ІІІ міні-модуль

Рефлексія

Обсяг і структура навчального модуля.

АДАПТИВНО – ПЕРЕТВОРЮВАЛЬНИЙ

МІНІ- МОДУЛЬ № 1 (30 хвилин)

  Повідомлення теми і мети уроку.   Мотивація навчальної діяльності.

 На попередніх уроках ми розглянули  теореми синусів, косинусів та наслідки з них, ввели поняття розв’язування трикутників, розглянули основні типи задач на обчислення елементів довільних трикутників, навчилися знаходити площу трикутника, використовуя різні формули.

Сьогодні  перед нами стоїть задача:

• повторити все, що вивчили;
• пригадати те, що забули;
• вміло застосовувати отримані знання до розв’язування геометричних задач.

Незважаючи на те, що попереду у нас велика пізнавальна робота, я сподіваюсь, що ми зможемо зберегти гарний настрій до кінця уроку, а якщо вдасться, то ще його й покращимо.

Перевірка домашнього завдання.

№ 5.12 – перевіряємо відповідь, згадуємо формулу для знаходження радіуса вписаного кола.

№ 5.14 – розбираємо план розв’язання задачі, звіряємо відповіді.

№ 5.28 – розв’язання записано на дошці, перевіряємо, коментуємо.

Питання до задачі:

- Які теореми було використано при розв’язуванні задачі?

- за якою формулою була обчислена площа трикутника?

Актуалізація опорних знань.

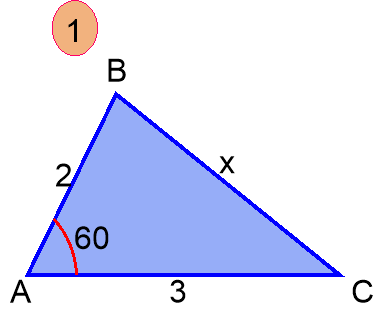
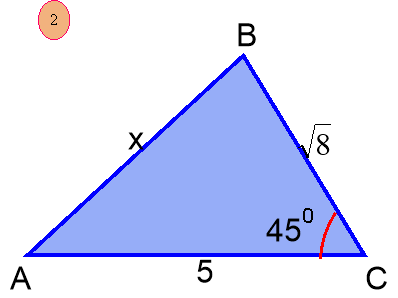
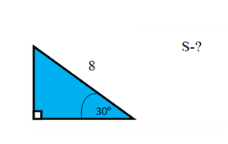
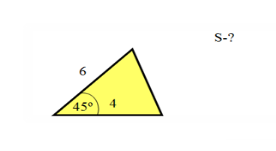
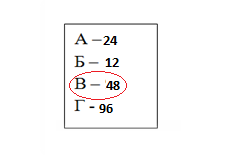
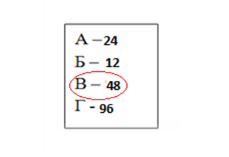
Відповідаючи на запитання, ми повторимо теоретичний матеріал з розділу «Розв’язування трикутників».

1)Що означає розв’язати трикутник?

2) Скільки елементів трикутника мають бути відомими, щоб його можна було розв’язувати?

3) Які теореми потрібно знати, щоб розв’язати трикутник?

4) Сформулюйте теорему косинусів.

5) Сформулювати теорему синусів.

6) Сформулюйте наслідок із теореми косинусів про співвідношення сторін трикутника.

7) Сформулювати наслідок з теореми синусів про діаметр кола, описаного навколо трикутника.

Знайдіть за малюнками 1 та 2 невідомий елемент трикутника. Які теореми було використане?

При вивченні теми ми з’ясували, що всі задачі на розв’язування трикутників можна поділити на чотири типи.

Задача

Сторони трикутника дорівнюють 6 см, 9 см, 8 см. Визначити вид трикутника.

Розв’язання.

Нехай АС=6 см, СВ=8 см, АВ=9 см. Вид трикутника визначаємо за найбільшим кутом, який, як ми знаємо, лежить проти більшої сторони. Отже нам треба знайти cosС.

Використовуючи теорему косинусів маємо:

АВ² = АС ^² + ВС ^² – 2АС ·ВС· cosС;

81 = 36 + 64 - 2 cos;

96 cos=19;

cos=. Оскільки знайдений  косинус є числом додатним ,то С- гострий

Відповідь: Трикутник – гострокутний.

АДАПТИВНО – ПЕРЕТВОРЮВАЛЬНИЙ

МІНІ- МОДУЛЬ № 2

                     ( 30 хвилин)

Розв’язування прикладних задач.

В сучасному житті потрібно бути компетентними у різних сферах: наприклад, порахувати кошторис для проведення ремонтних робіт в квартирі, розбити клумбу біля свого будинку тощо. Тому сьогодні ми розв’яжемо прикладні задачі з реального життя.

Прикладна задача – це задача, що виникла зовні математики, але для її розв’язування потрібно використати математичні моделі. Такі задачі розкривають багатогранність застосування математики в житті. Предмети, які нас оточують мають форму геометричних фігур. Вікна, двері наших будинків мають форму прямокутників і трикутників. Щоб споруди були стійкими і міцними, окремим їх деталям надають форму трикутника. Елементи, майже кожної будівельної конструкції виготовляють так, щоб вони мали якомога більше трикутників. Їх можна побачити у мостових формах, телевежах, кронштейнах.

Розв’язання.

АВС=180° - (80° +72° )= 28°. За теоремою синусів:

   ,      ;           ,  

Відповідь: 101,29 м.

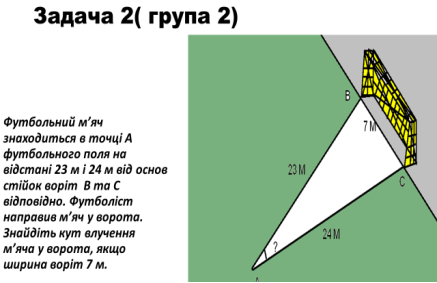
Розв’язання.

Розглянемо трикутник АВС, вершинами якого є точки А, В, С. За теоремою косинусів 

ВС² = АС² + АВ² – 2 ∙ АС ∙ АВ ∙ cos ВАС.

 ВАС – шуканий кут.

За наслідком із теореми косинусів cos ВАС = ,

cos ВАС = = 0,9565; ВАС=17°.

Відповідь: ВАС=17°.

Представники груп пропонують своє розв’язання.

Задача 3(ДПА 2017)

Сума двох сторін трикутника, кут між якими 60°, дорівнює 11 см, а довжина третьої сторони дорівнює 7 см. Знайдіть невідомі сторони трикутника.

                           В

         Хсм                            11-Х см

А                                                      С

                          7см

                          Розв’язання.

За теоремою косинусів маємо рівняння :

7² = Х² +(11-Х)² – 2Х(11-Х)cos60

Отримане рівняння учні розв’язують самостійно.

Перевіряємо відповіді.

Відповідь: 3см і 8см.

 Задача 3.( ДПА 2017)  - розв’язуємо з коментарями

Дві сторони трикутника відносяться як 5 : 3, а кут між ними дорівнює 120°. Знайдіть третю сторону трикутника, якщо його периметр дорівнює 45 см.

                                                    Відповідь: 21см

АДАПТИВНО – ПЕРЕТВОРЮВАЛЬНИЙ

МІНІ- МОДУЛЬ № 3

 (30 хвилин)

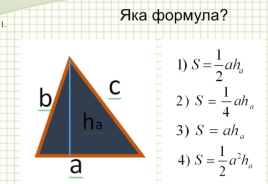
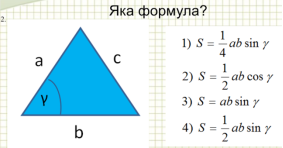
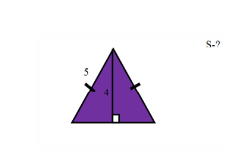
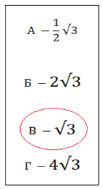
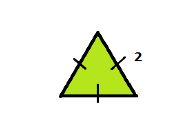
Останню частину нашого заняття ми присвятимо знаходженню площі трикутника. Ця тема є дуже важливою, бо кожний многокутник  можна розбити на трикутники. А розбивши фігуру на трикутники, можна легко знайти її площу як суму площ складених трикутників. До речі,так і робили єгипетські землеміри, визначаючи площі ділянок після розливу річки Нілу, а знаходити площу трикутника єгиптяни вміли вже кілька тисячоліть тому.

Для обчислення площі трикутника ми знаємо декілька формул, згадаймо їх.

Вправа   «Відгадай формулу» (вчитель показує рисунок трикутника, а учні відгадують формулу за якою можна обчислити його площу). (Формули на початку виконання завдання закриті та поступово відкриваються з відповідями учнів).

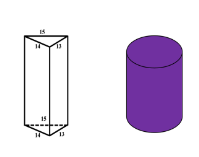
Задача. Із дерев'яного бруска , що має поперечний переріз у формі трикутника зі сторонами 13 дм, 14 дм, 15 дм, потрібно витесати і обточити циліндричний вал з найбільшим діаметром. Обчислити діаметр цього валу.

Відповідь: D = 8см

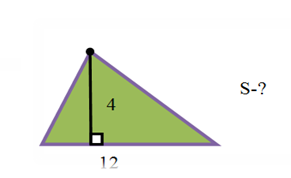
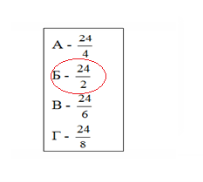
Задача. Відстань між трьома селами 4 км, 13 км, 15 км. На якій відстані від кожного села треба поставити вишку мобільного зв'язку, щоб прийом сигналу був однаковий у всіх трьох селах?

                   Відповідь. 8,125 км

А тепер перевіремо, як ви засвоїли формули для знаходження площі трикутника. Пропоную вам пройти тест.

1.

2.

3.                                                                      

4.

5.                                                                   

6.

Учні перевіряють свої результати, оцінюють свої успіхи.

Підсумок заняття. Домашнє завдання.

§ 1 п.2-5(повторити) № 5.16, 5.25

І на останок трохи цікавої інформації. Чи знаєте ви, є правило «золотого трикутника», яке використовують у торгівлі. Знайшовши в магазині потрібний товар, покупець, придбавши його, прямує до каси. Завдання продавця – змусити покупця затриматися в приміщенні магазину якомога довше. Для цього він (продавець) розташовує товар, який користується найбільшим попитом, у вершинах уявного трикутника (у різних кінцях магазину), а саме для того, щоб змусити покупця пройти весь периметр магазину. Чим більша площа трикутника між входом, касовим вузлом і товаром, тим більш вдалим можна назвати планування магазину і від цього збільшується об’єм продажів. 

Володіння теоретичними знаннями

Активізація регуляційно- вольової активності учня.

Зменшення напруження в ході створення алгоритмів

Осмислення добутих знань з метою розв’язування проблем

Накопичення досвіду.

Пошук істини, хвилювання