Тема уроку.   Ознака мимобіжності прямих.

Мета уроку: вивчення ознаки мимобіжності прямих, формування вмінь застосовувати ознаку мимобіжності двох прямих до розв'язування задач.

Обладнання: стереометричний набір, моделі тетраедра і куба.

Хід уроку

І. Перевірка домашнього завдання

1. Перевірити наявність виконаних завдань та відповісти на запитан­ня, які виникли в учнів під час виконання цих завдань.

2. Самостійна робота.

Варіант І

1) Трикутник АВС і паралелограм ABMN не лежать в одній площи­ні, К, L — середини сторін АС і ВС відповідно. Доведіть, що KL || MN . (4 бали)

2) Через кінці відрізка АВ і його середину Μ проведено паралельні прямі, що перетинають деяку площину в точках А₁, В₁, M₁. Знай­діть довжину відрізка АА₁, якщо ВВ₁ = b , MM₁ = т і відрізок АВ не перетинає площину. (8 балів)

Варіант 2

1) Паралелограми ABCD і ABMN не лежать в одній площині. Дове­діть, що CD || MN. (4 бали)

2) Через кінець А відрізка АВ проведено площину. Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетина­ють площину в точках В₁ і С₁. Знайдіть довжину відрізка СС₁, якщо АС = а, ВС = b, ВВ₁ = с. (8 балів)

Варіант 3

1) Паралелограм ABCD і трапеція ABMN (АВ — основа трапеції) не лежать в одній площині. Доведіть, що CD || MN. (4 бали)

2) Через кінець А відрізка АВ проведено площину. Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетина­ють площину в точках В₁ і С₁. Знайдіть довжину відрізка АС, якщо ВС = b, СС₁ = с, ВВ₁ = а. (8 балів)

Варіант 4

1) Трапеції ABCD і ABMN (АВ — основи трапеції) не лежать в одній площині. Доведіть, що CD || MN . (4 бали)

2) Через кінець А відрізка АВ проведено площину. Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетина­ють площину в точках В₁ і С₁. Знайдіть довжину відрізка АВ, якщо АС = a, ВВ₁ = b, СС₁ = с. (8 балів)

II. Сприйняття й усвідомлення нового матеріалу

Ознака мимобіжності прямих

Часто при розв'язуванні задач необхідно з'ясовувати: чи мимобіжні дані прямі? Користуючись означенням мимобіжності прямих, важко відповісти на це питання. Тому сформулюємо й доведемо ознаку мимобіжних прямих.

Теорема.

Якщо одна з двох прямих лежить у площині, а друга пере­тинає цю площину в точці, яка не лежить на першій пря­мій, то ці прямі мимобіжні.

Доведення

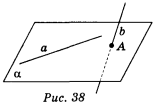
Нехай пряма а лежить у площині α , а пряма b перетинає цю площину в точці А такій, що А α (рис. 38). Доведемо, що прямі а і b мимобіжні. Припустимо, що прямі a і b не мимобіжні, тобто вони лежать в деякій площині β . Площина β проходить через пряму а і точку А і тому збігається з площиною α . Таким чином, пряма b лежить в площині α, що супере­чить умові. Отже, прямі a і b не лежать в одній площині, що і треба було довести.

Виконання вправ

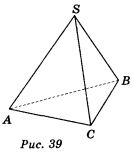
1. Дано в трикутнику піраміду SABC (рис. 39). Довести, що вказані прямі мимобіжні.a) SC і АВ; б) SB і АС; в) AS і ВС.

2. Дано куб ABCDA₁B₁C₁D₁ (рис. 40). Довести, що вказані прямі мимо­біжні.

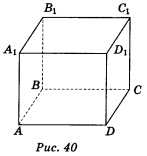а) АВ і СС₁;    б) АС₁ і DC;    в) AC і B₁D₁;     r) АС₁ і ВА₁.

3. Трикутники АВС і ABD не лежать в одній площині. Доведіть, що прямі АВ і CD не лежать в одній площині.

4. Пряма с перетинає пряму a і не перетинає пряму b, паралельну прямій а. Доведіть, що b і с — мимобіжні прямі.

III. Домашнє завдання

Вивчити ознаку мимобіжних прямих та розв'язати задачу № 27 (с. 20). З'ясувати, яке взаємне розміщення прямих AD₁ і АВ, DC і ВD₁ в цій задачі.

IV. Підведення підсумку уроку

Запитання до класу

1) Які прямі називаються мимобіжними?

2) Сформулюйте ознаку мимобіжності прямих.