Розробка уроку на тему "Теорема синусів"
Тема уроку. Теорема синусів.
Мета уроку: вивчення теореми синусів. Формування вмінь учнів застосовувати вивчену теорему до розв'язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця «Співвідношення між сторонами і кутами трикутника» [13].
Вимоги до рівня підготовки учнів: формулюють теорему синусів та доводять її.
Хід уроку
І. Перевірка домашнього завдання
Перевірити правильність виконання домашніх завдань за записами з пропусками.
Колективно обговорюється хід розв'язування задач і вписуються відповідні символи (записи). Там, де стоїть знак (?), необхідно пояснити, зробити посилання на відповідні теореми.
-
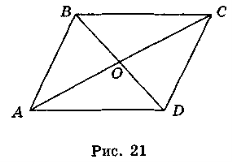
Нехай АС = с, BD = d,
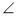AOB = α (рис. 21). Оскільки ABCD —
паралелограм, то АО = ..., ВО = ... (?).
За теоремою косинусів:
АВ2 = АО2 + ВО2 – 2АО ∙ ВО ∙ cosAOB = ... + ... - ... .
BOC = 180° - α (?).
ВС2 = ВО2 + СО2 – 2ВО ∙ CO ∙ cosBOC = ... + ... - ... .
Відповідь.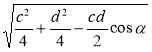 
, 
.
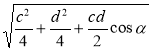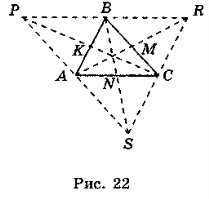
- Нехай АВ = 5 м, ВС = 6 м, АС = 7 м (рис. 22). АВRC — паралелограм. (?)
AR2 + BC2 = 2(AB2 + AC2) (?) 4АМ2 = - 36 + 2 ∙ (25 + 49) (?)
АМ2 = ..., АМ = .... АРВС — паралелограм. (?)
4СK2 + АВ2 = 2 ∙ (AC2 + BC2) (?) СК2 = ..., СК = ....
ABCS — паралелограм. (?) 4BN2 + ... = 2 ∙ (... + ...).
ВМ2 = ..., ВМ = ....
Відповідь. 
м, 2
м, 
м.
Самостійна робота
Варіант 1
- У трикутнику один із кутів становить 60°, а сторони, прилеглі до нього, дорівнюють a і b. Знайдіть третю сторону трикутника.
(4 бали)
- Сторони паралелограма дорівнюють 32 см і 10 см, а кут між ними становить 120°. Знайдіть діагоналі паралелограма.
(4 бали)
- Знайдіть діагоналі паралелограма, якщо вони відносяться як 3 : 5, а довжини сторін дорівнюють 8 см і 19 см.
(4 бали)
Варіант 2
-
У трикутнику дві сторони дорівнюють a і b, а кут між ними
становить 120°. Знайдіть третю сторону трикутника.
(4 бали)
- Діагоналі паралелограма дорівнюють 32 см і 10 см, а кут між ними становить 60°. Знайдіть сторони паралелограма.
(4 бали)
- Сторони паралелограма відносяться як 1 : 2. Знайдіть сторони паралелограма, якщо його діагоналі дорівнюють 18 см і 26 см.
(4 бали)
Відповіді до завдань самостійної роботи
Варіант 1. 1. a2 + b2 – ab. 2. 38 см і 2
см. 3. 15 см і 25 см.
Варіант 2. 1. a2 + b2 + ab. 2. 19 см і 
см. 3. 10 см і 20 см.
II. Сприймання й усвідомлення нового матеріалу
Вивчення теореми синусів
Наводимо пояснення теореми синусів.
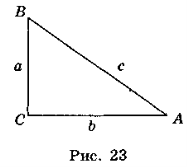
Розглянемо прямокутний трикутник ABC (рис. 23).
Відомо, що а = c sinA, b = c sinB, звідси 
, 
. Тоді 
. Ураховуючи, що C = 90° і sinC = 1, запишемо:
.
Якщо описати коло радіуса R навколо прямокутного трикутника ABC (рис. 24), то одержимо: 
.
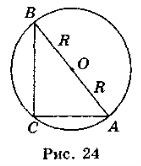
Отже, у прямокутному трикутнику сторони пропорційні до синусів протилежних кутів.
А чи є це твердження правильним для будь-якого трикутника?
Спочатку з'ясуємо співвідношення між діаметром кола, стороною вписаного в нього трикутника і кутом трикутника, протилежним цій стороні.
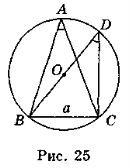
Нехай у трикутнику ABC кут А гострий, ВС = а (рис. 25). Проведемо діаметр BD, який дорівнює 2R, R — радіус описаного кола.
Сполучивши точки D і С, одержимо прямокутний трикутник BDC, у якому ВС є катетом, і тому BC = BDsinD. Але D = А як вписані, що опираються на дугу ВС, і тому sinD = sinA.
Отже, a = 2RsinA.
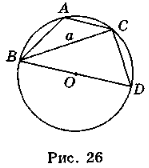
Одержане співвідношення справджується й тоді, коли кут А тупий (рис. 26), оскільки A + D = 180°. Тоді D = 180° - A і sinD = sin(180°- А). Таким чином, а = ВС = BDsinD = 2RsinD = 2RsinA.
Отже, завжди a = 2RsinA.
Аналогічно переконуємося, що b = 2RsinB, c = 2RsinC. У кожній із трьох останніх рівностей виразимо відношення сторони до синуса протилежного кута:
; 
; 
.
Отже, 
.
Таким чином, сторони трикутника пропорційні до синусів протилежних кутів, відношення сторони трикутника до синуса протилежного кута дорівнює діаметру кола, описаного навколо трикутника.
Розв'язування задач
- Сторона трикутника дорівнює 20 см, а протилежний кут становить 150°. Знайдіть радіус кола, описаного навколо трикутника. (Відповідь. 20 см.)
-
Знайдіть сторону АВ трикутника ABC, якщо ВС = 2
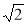см, 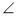A = 45°, 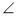C = 30°. (Відповідь. 2 см.)
III. Закріплення й осмислення вивченого матеріалу
Колективне розв'язування задачі
1) У трикутнику ABC АВ = 15 см, АС = 10 см. Чи може sinβ = 
?
Розв'язання
Припустимо, що sinβ = 
. Тоді з рівності 
, враховуючи, що АВ = 15 см, АС = 10 см, матимемо: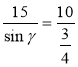 
. Звідси sinγ = 15 ∙ ∙ 
= 
> 1, що неможливо (бо sinγ < 1).
Отже, sinβ не може дорівнювати .
Відповідь. Не може дорівнювати.
2) У трикутнику задано дві сторони а = 27, b = 9 і кут, протилежний до однієї із сторін, α = 138°. Знайдіть два інші кути і третю сторону трикутника.
Розв'язання
; 
; 
; β 
13°. Тоді γ = 180° - α - β 180° - 138° - 13° = 29°.
; 
; 
.
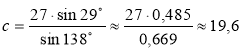Відповідь. β 13°, γ 29°, с 19,6.
Задачі для індивідуального розв'язування
- У рівнобедреному трикутнику основа дорівнює а, а кут при основі дорівнює 2β. Знайдіть бісектрису трикутника, проведену до бічної сторони.
Відповідь. 
.
- У прямокутному трикутнику гіпотенуза дорівнює с, а один із гострих кутів дорівнює α. Знайдіть бісектрису прямого кута.
Відповідь. 
.
- Доведіть, що сторона трикутника, яка лежить проти кута в 30°, дорівнює радіусу кола, описаного навколо цього трикутника.
- Доведіть, що бісектриса кута трикутника ділить протилежну сторону на відрізки, що обернено пропорційні синусам прилеглих до цієї сторони кутів.
Доведення
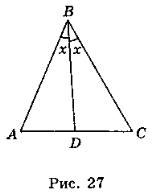
Нехай у трикутнику ABC (рис. 27) BD — бісектриса і ABD = DBC = x.
Із трикутника ABD за теоремою синусів маємо: 
. (1)
Із трикутника BDC за теоремою синусів маємо: 
. (2)
Розділивши рівність (1) на рівність (2), одержимо 
, що й треба було довести.
IV. Домашнє завдання
- Вивчити теорему синусів.
- Розв'язати задачу.
У трикутнику дано дві сторони і кут, протилежний до однієї із сторін. Знайдіть інші два кути і третю сторону трикутника, якщо:
а) а = 12, b = 5, α = 120°; б) а = 34, b = 12, α = 164°.
V. Підбиття підсумків уроку
Завдання до класу
- Сформулюйте теорему синусів.
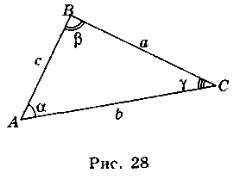
- У трикутнику ABC (рис. 28) сторони дорівнюють a, b, c, a кути дорівнюють α, β, γ. Навколо цього трикутника описане коло радіуса R. Які з наведених тверджень є правильними, а які — неправильними?
a) b = 2Rsinα; б) 
; в) 
; г) 
.
про публікацію авторської розробки
Додати розробку