План-конспект уроку

 

Тема: Розвиток математики в Китаї, Індії та Арабському халіфаті

Мета: ознайомити із історією розвитку математики в Китаї, Індії та Арабських країнах, основними фактами та відомостями.

Вид заняття: урок.

 

Хід заняття

І. Організаційний момент

IІ. Повідомлення теми та мети. 

ІІІ. Викладання нового матеріалу

План

1. Історія розвитку математики в Китаї.
2. Історія розвитку математики в Індії.
3. Історія розвитку математики в арабських країнах.

 

1. Історію розвитку математики в Китаї розглянемо за такими пунктами:

1.Математична освіта в Китаї.

2.Китайська «символіка».

3.Видатні математики ХІІІ ст.: Цинь Цзю-шао, Лі Є, Ян Хуей, Чжу Шицзе.

4.Розв’язання систем лінійних рівнянь у Китаї (книги 7 і 8 ).

5.Розв’язування прямокутних трикутників (книга 9, роботи Лю Хуея).

6.Арифметичний посібник Сяхоу Яна.

 

1.     Математична освіта в Китаї

Періоди розвитку математики в Китаї

Якісне представлення про загальний розвиток математики дає періодизація, запропонована академіком А. Н. Колмогоровим. Згідно з його періодизації, виділяються чотири етапи:

1.               накопичення математичних знань і створення практичної математики;
2.               період елементарної математики, або математики постійних величин;
3.               створення математики змінних величин;
4.               період сучасної математики.

Китайська математика цілком укладається в другий період розвитку, період математики постійних величин. Відзначаються тому окремі найбільш яскраві відкриття китайських вчених:

- Метод чисельного рішення рівнянь n-ступеня (метод Руффини - Горнера);

- Теоретико-числові завдання на системи порівнянь першого ступеня з одним невідомим (порівняння Гаусса);

- Метод рішення систем лінійних рівнянь (метод Гаусса);

- Обчислення числа π (пі).

Китайська техніка рахунку була заснована на десяткової нумерації, але користувалися позиційним принципом. У стародавньому Китаї велику роль грала лічильна дошка з здійсненої на ній позиційною системою числення.

Поняття числа. Арифметичні та теоретико-числові проблеми.

Тут розглядається алгебраїчний шлях переходу від цілих чисел до чисел раціональним. Той історичний процес, який відбувався в стародавньому Китаї при освоєнні поняття числа, носив досить загальний характер і мав місце у всіх стародавніх цивілізаціях:

- Звичайні дроби;

- Пропорції і прогресії;

- Проблема розподілу із залишком.

Алгебра. Рішення рівнянь.

Алгебраїчні методи характерні для китайської математики. Досягнення китайських алгебраїстів - найбільш відома частина історії математики в Китаї, відома, проте не повною мірою. Зауважимо, що давня алгебра викладалася словесно, без символіки:

- Лінійні системи;

- Рішення рівнянь вищих ступенів чисельним методом;

Геометрія. Застосування методів алгебри до геометричних завданням.

Тут розглядалися методи, якими користувалися при вирішенні різних завдань прикладного характеру. Існує обгрунтований погляд на китайську математику як на обчислювальну, для якої характерні алгебраїчні методи:

- Вимірювання площ і об'ємів;

- Теорема Піфагора;

- Вимірювання кола і кулі;

- Визначення відстаней до недоступних предметів.

2. Китайська символіка

 Додатні кількості в китайській математиці назвали «чен», від'ємні — «фу»; їх зображали різними кольора­ми: «чен» — червоним, «фу» — чорним. Такий спосіб зображення використовувався в Китаї до середини XIII ст., поки Лі Є не запропонував зручніше позначення від'ємних чисел — цифри, що зображали від'ємні числа, перекреслювали рискою навскіс справа наліво

Цифри позначалися спеціальними ієрогліфами, які з'явилися в II тисячолітті до н. е.., і знамено їх остаточно встановилося до III в. до н.е.. Ці ієрогліфи застосовуються і в даний час. Для запису великих чисел в стародавньому Китаї використовувалися 4 різні системи. Перша система є, очевидно, найдавнішою. Зараз повсюдно використовується друга система, та більшість людей не знають символів, великих.

Цифри в стародавньому Китаї позначалися спеціально розробленими ієрогліфами, накреслення яких остаточно встановилося до кінця третього століття до н.е. Цікавий той факт, що ці ж ієрогліфи використовуються і донині.

На  практиці розрахунки виконувалися на лічильній дошці суаньпань, де запис чисел був іншим — позиційним. Сучасний тип цього приладу створили пізніше, очевидно в XII столітті. Китайці розробили техніку роботи лічильної дошки. Виконували всі 4 арифметичні операції, і навіть видобувати квадратні і кубічні коріння.

3.     Видатні математики XIII ст.: Цинь Цзю-шао, Лі Є, Ян Хуей, Чжу Шицзе

Цінь Цзю-шао (秦九韶, 1208 —1261) — китайський математик часів династії Сун, один з великих алгебраїстів XIII ст.

Цінь Цзю-шао у 1244–1247 роках написав свою головну працю, яка в епоху Сун називалася «Шусюе далюе» або «Шушу далюе», а в епоху Мін — «Шусюе цзючжан» або «Шушу цзючжан» («Книга про числа в дев'яти розділах»).

За формою трактат нагадує «Цзючжан суаньшу», але більш складний і в архітектоніці цілком свідомо пронумерований. У ньому 81 завдання розподілена по 9 «родам» (лей). Кожна задача супроводжується відповіддю, «правилом» (шу), що містить метод, і «рішенням» (цао), що вказує послідовність дій, а при необхідності і пояснювальній схемою.

I розділ - присвячено невизначеному аналізу та рішенню по модулю системи порівнянь першого ступеня з одним невідомим.

II розділ («Небесні часи» )-про астрономію, календарі та метеорологію

III розділ («Площі полів» )-наведена важлива формула, яка виражає площу геометричної фігури як корінь рівняння четвертого ступеня. формула площі трикутника, дана у термінах його сторін: A = √ ¼ [a²b² — ½ (a² + b² — c²)²] і еквівалентна формулі Герона.

IV розділ («Виміри здалека» )- включає завдання на вимірювання відстаней з недоступних точок з використанням рівнянь вищих ступенів аж до десятої.

V-IX розділ -Розглядаються лінійні системи рівнянь, вирішення низки завдань приводяться до рівнянь третьої або четвертої ступенів прототипом методу Руффіні-Горнера.

Лі Е (李冶,1192-1276) — китайський математик часів династії Дзінь та Юань.

Лі Е написав 10 книг. Однак, будучи при смерті, він наказав синові всі їх спалити, крім «Це юань ганьбі цзін», яка, як він вважав, одна могла бути корисною наступним поколінням, але збереглася також «І гу янь дуань».

Книга «Це юань ганьбі цзін» («Морське дзеркало вимірювань кола»), яка була написана у 1248 році, присвячена здебільшого рішенням рівнянь, що стосуються кіл, вписаних в трикутники. Вона починається з передмови, в якій подається єдине у книзі креслення кола, вписаного в прямокутний трикутник, в якому різного роду лінії (проведені через центр кола, дотичні та ін.) утворюють 15 прямокутних трикутників різних розмірів. На цьому кресленні ґрунтуються 170 завдань, поміщених у главах від 2 до 12. Глава 1 є довідковою. Ця книга — найраніше джерело методу тянь юань («небесного невідомого»). У своїй роботі Лі Е не пояснював, як розв'язувати рівняння, і що розуміється під рівнянням, невідомим, негативним числом і ін., а лише показував, як будувати рівняння, не обмежуючись другою або третьою ступенями і займаючись рівняннями доволі високих ступенів. Він використовував метод, подібний до методу Руффіні-Горнера, який був розроблений більш ніж шістьма століттями пізніше. Ця книга справила сильний вплив на японську математику, зокрема на дослідні Секі Кōва.

Ян Хуей (杨辉, 1238 —1298) — китайський математик з групи визначних сунських алгебраїстів XIII–XIV ст., педагог-методолог.

Займався десятковими дробами, магічними квадратами, рядами, арифметичній прогресії, системами рівнянь і «правилом сумішей».

Сформулював аналог доказу теореми Евкліда про паралелограми й уперше використав циклічні знаки (ганьчжі) як алгебраїчні позначення невідомих у лінійних системах. Критикував математиків, які «змінюють назви своїх методів від задачі до задачі».

У 1261 році написав «Сянцзе цзючжан суаньфа» («Докладне роз'яснення методів числення в дев'яти розділах“) у 12 цзянів з додатком „Цзючжан суань фацзуань лей“ („Методи числення в дев'яти розділах у послідовній класифікації»). Кожна задача розглянута в трьох аспектах: її логіки, числового розв'язку, застосування представленого методу розв'язку для інших подібних завдань.

Чжу Шицзе (朱世杰, 1249 — 1314) — китайський математик-алгебраїст часів династії Сун та Юань.

У 1299 році у зв'язку з великою кількістю учнів склав «Суаньсюе цимен» («Вступ до вчення про рахунок»). Згодом, у 1303 році, створив значніший твір «Сиюань юйцзянь» («Нефритове свічадо чотирьох першоелементів»).

«Вступ до вчення про рахунок» незабаром після видання загубився в Китаї, але, потрапивши до Японії і Кореї, був там вперше надрукований відповідно у 1433 та 1658 роках й використовувався як підручник з математики. На батьківщину він потрапив у XIX ст., коли у 1839 році його було переведено китайською з японської мови.

Вперше теоретично оформлені правила перемноження позитивних і негативних чисел, введені нові поняття, пов'язані з перемножуванням зворотних чисел, дані приклади обчислень з дробами і десятковими числами, пояснення потрійного правила, правила помилкової подвійний позиції і правил обчислення площ та об'ємів. При роботі з системами рівнянь зроблені уточнення, по суті, еквівалентні методом Гаусса.

4.     Розв’язання систем лінійних рівнянь у Китаї

Хоч окремі задачі, які можна тлумачити як системи лінійних рівнянь, зустрічаються ще в стародавніх вавилонських текстах, - загальний метод розв’язування систем лінійних рівнянь вперше досить детально розробили китайські математики. Виклад цього методу можна знайти в одному з найперших відомих китайських математичних творів – “Математика в дев’яти книгах” (ІІ – І ст. до н.е.), в якому підведені підсумки багатовікового розвитку математичних знань у Китаї. Отже, теорія лінійних алгебраїчних рівнянь має стародавні джерела.

Стародавній китайський метод подано у формі певного способу розв’язування конкретних арифметичних задач, але по суті він має загальний алгебраїчний характер і збігається з сучасним методом виключення невідомих за допомогою зрівнювання коефіцієнтів.

Метод “фан-чен” зустрічається і у відомому математичному трактаті китайського математика Сунь-цзи (III – IV ст. н.е.). В 1683 р. японський математик КоваСекі удосконалив цей метод, наблизивши його до ідей теорії детермінантів. Тоді ж, в кінці XVII ст., до проблеми знаходження загальних формул розв’язків систем лінійних рівнянь звернувся видатний німецький математик і філософ Г.В. Лейбніц (1646  - 1716). Саме Лейбніц запровадив для позначення коефіцієнтів лінійної системи два індекси і завдяки цьому дістав основні правила побудови чисельників і знаменників формул розв’язків (тобто по  суті – детермінантів).

 

5.     Розв’язування прямокутних трикутників (Книга 9, роботи ЛюХуея)

Лю Хуей (刘徽, 220 — 2280) — китайський математик часів династії Вей.

Народився у 220 році. Про його життя майже немає відомостей. Походив зі знатного роду, був нащадком аристократа Ціаня. Ймовірно більшу частину життя мешкав у столиці держави Вей — Лояні, знаходячись у почті імператорів з роду  Цао. Помер у 280 році.

У 263 році він написав коментар до «Цзю чжансуань шу» («Правила рахунку в дев'яти розділах») та книгу «Хай даосуаньцзин» («Лічильний канон морського острова»).

У коментарі до «Правила рахунку в дев'яти розділах» за допомогою спеціальних методів Лю Хуей обчислював площу кола і об'єми різних тіл типу призми, піраміди, тетраедра, клину, циліндра, конуса і зрізаного конуса. Безуспішно намагаючись знайти об'єм кулі, він написав, що залишає цю роботу майбутнім математикам. На відміну від своїх попередників, яким булла властива догматична подача математичного матеріалу, Лю Хуей зробив перші теоретичні кроки, забезпечивши поясненнями алгоритмічні правила з «Правила рахунку в дев'яти розділах».

«Лічильний канон морського острова») — спеціальний твір з практичної геометрії, що складається з дев'яти задач на визначення відстані до недоступного об'єкта і його розмірів (висота острова, сосни, вежі, ширина гір, стіни, річки, глибина ущелини, ями) за допомогою застосування прямокутного трикутника та його властивостей. Для всіх задач наводиться правильний розв'язок і відповідь. Для обчислень використовуються від 2 до 4 вимірювань за допомогою пари жердин (бяо), пари косинців (цзюй) абомотузки (зі). Лю Хуей розв'язує задачі за допомогою розробленого ним методу чунча («подвійнарізниця»), назва якого пояснюється використанням відношення двох виміряних різниць, отриманих на підставі подібності прямокутників.

6. Арифметичний посібник Сяхоу Яна

Текст відноситься до середині VI ст. Трактат складається з трьох книг, він виділяється особливим прагненням до полегшення виробництва операцій на рахунковому приладі. Всього 73 завдання, причому в першій книзі немає завдань.

Про «Математичний трактат Сяхоу Яна» («Сяхоу Ян суань цзин») дослідники зазвичай згадують у зв’язку з творами Сунь-цзи і Чжан-цзяня, коротко описуючи його зміст таким, який зводиться до задач на відсотки, до операцій множення та ділення і принципу позиційності. Відомо, що в передмові трактата Чжан Цю-цзяня (V ст.. н. е.) згадується про Сунь-цзи і Сяхоу Яна, а в трактаті Сяхоу Яна повторюється правило знаходження площі неправильного чотирикутника, яке вжито в «Математичному трактаті п’яти відомств». Це все, що відомо про хронологію тексту. Про автора трактата також немає відомостей.

Книга перша трактату Сяхоу Яна містить опис принципу позиційності китайської лічильної дошки, деяких правил операцій (множення і ділення) з цілими числами і дробами, метрологічних таблиць та ін. Однак на відміну від трактату Сунь-цзи у Сяхоу Яна в першій книзі для пояснення деяких правил наводяться завдання . Їх всього дев'ять. У Сунь-цзи завдань в першій книзі немає. Але в ньому велику частину займають числові таблиці, яких у Сяхоу Яна немає зовсім. Весь матеріал першої книги трактату Сяхоу Яна розділений на окремі параграфи. Їх налічується шість. Це теж нововведення в манері викладу древніх авторів.

Слід відзначити ще одну характерну особливість трактату Сяхоу Яна: у першій його книзі здійснюється спроба описати історію еталонів мір і ваги, чітко сформулювати правило множення і ділення на ступені 10, яке, щоправда, вживалося ще до Сяхоу Яна, наприклад у Сунь-цзи.

З усіх трактатів «Десятикнижжя» твір Сяхоу Яна виділяється особливим прагненням до полегшення виробництва операцій на рахунковому приладі. Дуже часто в задачі дається два способи вирішення, що відрізняються один від одного тим, що в одному з них спеціально описаний спосіб швидкого рахунку.

 

2. Історію розвитку математики в Індії розглянемо за такими пунктами:

1.Математика в Стародавній Індії як наука про обчислення (способи запису чисел, нуль, правила виконання дій, …).

2.Особливості геометричних знань в Індії.

3.Математичні здобуткиАріабхати

4.“Удосконалена наука Брахми”.

5.Математичні здобуткиМагавири.

6.«Вінок науки» Бхаскари.

7.Розвиток тригонометрії в Індії.

8.Життєвий шлях і творчість Сринивази Ромамуджана.

9.Квадратні рівняння в Індії.

10.Математика сучасної Індії. Міжнародні премії для індійських математиків.

 

 

 

1. Математика в Стародавній Індії як наука про обчислення

Спочатку, за свідченнями найдавніших текстів санскриту, для запису чисел в Індії використовувалися слова: одиниця – «місяць», «земля»; двійка – «очі», «губи»…І лише потім з’явилися позначення цифр.

Цифри мали вигляд початкових букв відповідних числівників на давньоіндійській мові - санскриті (алфавіт «девангарі»).

Спочатку цими знаками представлялися числа 1, 2, 3, ..., 9, 10, 20, 30, ..., 90, 100, 1000; з їх допомогою записувалися інші числа. Після винайдення числа нуль, знаки для чисел, більших 9, вийшли з ужитку, і нумерація «девангарі» перетворилася в десяткову помісну систему.

Цифрові знаки Індії не співпадають за формами з сучасними цифрами, але все ж мають з ними в деяких випадках велику схожість. Так, наприклад, дуже схожі на сучасні цифри індійські знаки, що зображали одиницю і сімку. Інші знаки протягом багатьох віків, що відділяють нас від часу їх виникнення, сильно видозмінилися. 

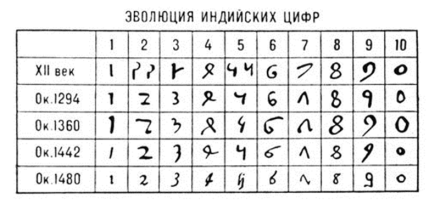
Позиційне числення дуже поширилося через те, що люди мали природну лічильну машину» — десять пальців на руках.

Як говорив видатний російський математик М. М. Лузін (1883—1950), «Переваги десяткової системи не математичні, а зоологічні. Якби в нас на руках було не десять пальців, а вісім, то людство користувалося б вісімковою системою».

Аналогічно щодо цього висловився відомий французький математик А. Лебег (1875—1941): «Можливо, що, коли б люди мали 11 пальців, була б прийнята одинадцяткова система числення».

Видатний французький математик і фізик Лаплас (1749—1827) писав: «Думка подати всі числа дев’ятьма знаками, надаючи їм, крім значення за формою, ще й значення за місцем, така проста, що саме внаслідок цієї простоти важко зрозуміти, наскільки вона чудова. Як нелегко було прийти до цього методу, ми бачимо на прикладі великих геніїв грецької науки Архімеда і Аполлонія, які до цього не дійшли».

Дуже скоро стало потрібним введення нового числа - нуля. Учені розходяться в думках, звідки до Індії прийшла ця ідея - від греків, з Китаю або індійці винайшли цей важливий символ самостійно. Нуль, що називався «сунья», або - ніщо, зображали спочатку у вигляді крапки, а пізніше у виді маленького кружечка.

Введення нуля, цифр і їх позиційного принципу полегшило обчислювальні операції над числами, а тому арифметичні обчислення і отримали в Індії значного розвитку.

2. Особливості геометричних знань в Індії

Знання та відкриття індійських математиків в геометрії скромніше, ніж в арифметиці, алгебрі та теорії чисел. Спеціальних творів з геометрії в Індії не було, ці відомості повідомлялися в арифметичних трактатах або в арифметичних розділах творів з астрономії.      

Геометричні теореми наводилися без доказів. Зазвичай це було тільки креслення зі словом «дивись». Лише в окремих випадках його супроводжували короткі пояснення. Мабуть, докази учням повідомлялися усно. У геометричних задачах питання частіше всього зводилися до обчислень і набагато рідше - до побудов.

Найбільш ранні відомості про пізнаннях індійців у галузі геометрії є в посібнику з будівництва вівтарів і храмів - «Шульба-сутрі». Храми зводили, підкоряючись ряду правил: будівлі повинні були мати в основі певні фігури і бути зорієнтовані на сторони світу. Для цього було потрібно вміння будувати прямий кут, квадрат, прямокутні трикутники, сторони яких виражаються цілими числами. Індійці знали, як побудувати квадрат, рівновеликий прямокутнику, і квадрат, площа якого кратна площі даного квадрата. Відправною точкою багатьох побудов служила теорема Піфагора.

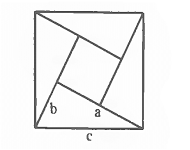
Бхаскара навів доказ теореми Піфагора у вигляді креслення з надписом: «дивись».

Якщо позначити катети прямокутного трикутника через a та b, побудованого на кожній із сторін квадрата, а гіпотенузу через с і рівну стороні квадрата, то площа квадрата буде рівна чотирьом  площам  прямокутного трикутника і площі квадрата побудованого на різниці катетів трикутника.  Спростивши отримаємо співвідношення .

3. Математичні здобутки Аріабхати

Аріабхата I (476- бл. 550 до н.е.) - індійський астроном і математик. Народився у великому науковому центрі Кусумапура. У творі "Аріабхати" (499), присвяченому астрономії та математики, викладені математичні відомості, необхідні для астрономічних спостережень. Аріабхата висловив здогад про те, що Земля обертається навколо осі і навколо Сонця. У творі Аріабхати зустрічаються вилучення квадратних і кубічних коренів з чисел, найпростіші завдання на складання і рішення рівнянь, зокрема на рішення одного рівняння з двома невідомими в цілих числах, підсумовування кубів натуральних чисел; з геометричних відомостей наводиться наближене значення числа π = 3,1416.

Роль Аріабхати у розвитку індійської математики та астрономії величезна.

  Аріабхата написав два твори: перше і єдине що дійшло до нас - «Аріабхати», друге - коментарі до астрономічного твору «Сурьясіддханта». Цей твір не зберігся. «Аріабхати», написаний у віршах, складається з чотирьох частин: перша присвячена системам позначення чисел, друга - математиці, третя і четверта носять переважно астрономічний характер, хоча вони містять математичні відомості. Цей трактат був написаний в 499 році, коли автору було 23 роки.

В  математиці:

•              описав процес добування квадратного і кубічного коренів;
•              навів кілька завдань на лінійні рівняння з одним невідомим;
•              знаходження числа членів арифметичної прогресії;
•              першим прийняв π рівним 3,1416;
•              у його трактаті зустрічаються синус і косинус, а також перша в Індії таблиця синусів

В теорії чисел:

•              першим сформулював методи вирішення в цілих числах невизначеного рівняння першого ступеня з двома невідомими;
•              навів правила підсумовування рядів трикутних чисел, натуральних квадратів і кубів, натуральних чисел.

В астрономії:

•               навів діаметри Землі, Сонця, Місяця та інших небесних тіл;
•               дав відомості календарного характеру;
•               способи інтерполяційних обчислень;
•               висловив здогад, що Земля обертається навколо своєї осі і навколо Сонця.

4. «Удосконалена наука Брахми»

Брахмагупта, Брамагупта (санскр. ब्रह्मगुप्त, бл. 598-670) - індійський математик і астроном. Керував обсерваторією в Удджайні. Зробив істотний вплив на розвиток астрономії у Візантії та ісламських країнах, став використовувати алгебраїчні методи для астрономічних обчислень, ввів правила операцій з нулем, додатними і від’ємними величинами.

Брахма-спхута-сіддханта.«Брахма-спхута-сіддханта» («Удосконалена наука Брахми», або «Перегляд системи Брахми») - найвідоміша праця Брахмагупти, присвячена математиці та астрономії. Трактат написаний віршами і містить тільки результати без доведень. Праця складається з 25 глав (в інших джерелах говориться про 24 глави і додаток з таблицями).

Перші 10 розділів містяться зокрема розрахунки середньої та дійсної довготи, обчислення добового обертання, розрахунок сонячних і місячних затемнень, методи розрахунку положення небесних тіл з плином часу (ефемериди), їх сходів і заходів, з'єднань.

Наступні 15 глав містять значні доповнення та уточнення до перших глав, а також глави з математики. Математичні глави дають уявлення про два основні підходи індійських математиків: «математика процедур», або алгоритми, і «математика насіння», або рівняння. 12-а глава книги носить назву «Математика», вона присвячена простим арифметичним операціям, пропорціям, задачам на змішування і рядам, що становило основну частину практичної математики в часи Брахмагупти. 18-а глава, «Розпилювач», має пряме відношення до алгебри, але оскільки такого терміну ще не існувало, названа по першій задачі, розглянутій в розділі.

Внесок у математику. У своїй роботі Брахма-спхута-сіддханта Брахмагупта дав визначення нуля як результат віднімання з числа самого числа. Він одним з перших встановив правила арифметичних операцій над додатними і від’ємними числами і нулем, розглядаючи при цьому додатні числа як майно, а від’ємні числа як борг. Далі Брахмагупта намагався розширити арифметику давши визначення ділення на нуль. Згідно Брахмагупти:

• ділення нуля на нуль є нуль;
• ділення додатного або від’ємного числа на нуль є дріб з нулем в знаменнику;
• ділення нуля на додатне чи від’ємне число є нуль.

Брахмагупта запропонував три методи множення багатозначних чисел в стовпчик (основний і два спрощених), які близькі до тих, що використовуються в даний час. Брахмагупта також запропонував метод наближеного обчислення квадратного кореня, еквівалентний ітераційної формулою Ньютона (Newton-Raphson), метод розв'язання деяких невизначених квадратних рівнянь виду     ax² + c = y², метод розв’язання  невизначених лінійних рівнянь виду ax + c = by, використовуючи метод послідовних дробів.

Тотожність Брахмагупти

Тотожність Брахмагупти стверджує, що добуток двох сум двох квадратів саме є сумою двох квадратів, причому двояким чином.

Наприклад,

5.               Математичні здобутки Магавири

Махавіра (mahAvIra, букв. ,, великий герой,,) – представник дігамбарської вітки джайнізма, що жив в сер. 9 ст. н. е. Він працював при дворі Амогхаварші (роки правління 815- 877), царя із династії Раштракутов – правителів великої імперії (8-10 ст.), що знаходь. на території сучасних штатів Каратака і Махараштра.

Трактак Махавіри ,, Збірник основних положень науки про обчислення’’ (gaNitasArasaGgrahaH) – єдина відома праця Махавіри. Цей трактат є першим в історії індійських думок роботою, в якій мова йде лише про математику як незалежну ( перш за все від астрономії) дисципліну. В даному трактаі містяться майже всі математичні досягнення того часу. Впродовж багатьох століть трактат,, Збірник основних положень науки про обчислення’’ (gaNitasArasaGgrahaH) користувався успіхом серед вчених всієї Індії.

В трактаті мова йде про : арифметичні операції, дії з дробами, арифметична та геометрична прогресії,  правило трьох величин, задачі на рух, економічні задачі, комбінаторика, розв’язання систем рівнянь з декількома змінними, планіметрія, стереометрія та ін. В трактаті Махавіра дає правила обчислень ( без доведень).

Трактат ,, Збірник основних положень науки про обчислення’’ (gaNitasArasaGgrahaH) написаний на санскриті, в традиційно індійському стилі – у віршах. Текст складається з 9 глав. Матеріал розподілений нерівномірно, а саме : 1 гл. – 70 в, 2 гл. – 115 в., 3 гл. – 140 в., 4 гл. – 72 в., 5 гл. – 43 в., 6 гл. – 337 в., 7 гл. – 232 в., 8 гл. – 68 в., 9 гл. – 52 в. Всього 1129 віршів.

 6. «Вінок науки» Бхаскари

Бхаскара (1114-1185), зазвичай називають Бхаскар II, щоб відрізнити його від іншого індійського вченого Бхаскар I) - великий індійський математик і астроном XII століття. Очолював астрономічну обсерваторію в Удджайне.

Бхаскара написав трактат «Сиддханта-шіромані» («Вінець вчення»), що складається з чотирьох частин: «Лілаваті»-«Красуня» присвячена арифметиці, «Біжда-ганіта»-«Обчислення коренів» - алгебрі, «Голадхайя» - Сферика, «Гранхаганіта» - теорії планетних рухів. Праця «Вінець вчення» є вершиною розвитку індійської математики. Найцікавіші дві перші частини цього твору – «Лілаваті» і «Біжда-ганіта».

У них викладені методи розв`язання алгебраїчних задач , що зводяться до рівнянь першого степеня, правила дій над додатними та від`ємними числами, правила розв`язання невизначених рівнянь першого і другого степенів у цілих числах, прикади розв`язування систем нелінійних рівнянь та окремих рівнянь 3 і 4 степенів.

Здобутки:

А) розв`язує в цілих числах , яке пізніше дістало назву «рівняння Пелля»;

Б) розв`язує систему

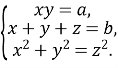
В) Розглядає тотожності, які пізніше включалися майже в усі математичні навчальні підручники і посібники:

і

Бхаскара отримував від`ємні корені рівнянь, хоча і сумнівався в їх значущості. Йому належить один з найбільш ранніх проектів вічного двигуна.

7. Розвиток тригонометрії в Індії

Вчення про тригонометричні функції почало розвиватися ще у 4 – 5 столітті у працях індійських вчених. Тригонометрія у індійців розвивалася головним чином у зв’язку з її астрономічними додатками, загалом для використання в теорії руху планет і для вивчення небесної сфери. Це свідчить про хороше знання сферичної тригонометрії «Альмагеста» і «Аналемми», проте ні одної власної їх роботи, яка розвиває теорію цього розділу тригонометрії, не знайдено.

Проте, в розробці прикладних алгоритмів розв’язування астрономічних задач індійці досягли великих успіхів. Наприклад, в «Панча-сіддхантіке» Варахаміхири ( 7 ст.) дається оригінальний розв’язок астрономічної задачі, описаної у Птолемея: знайти висоту Сонця над горизонтом, якщо відомі широта місцевості, схилення Сонця і його годинний кут. Автор для розв’язання застосовує  аналог теореми косинусів, він же вперше привів формулу для синуса половинного кута.

Для астрономічних розрахунків був створений ряд тригонометричних таблиць. Перші таблиці синусів наведені в стародавній «Сурья-сіддханте» і у Аріабхати (5 століття).

В 11 столітті мусульмани (Махмуд Газневі) захопили і розорили Північну Індію. Культурні центри перемістилися в Південну Індію, де виникла «школа Керала», що в 15 – 16 століттях досягла великих успіхів в області додавання тригонометричних функцій; дала правила розкладення синуса і косинуса в нескінченні степеневі ряди; привела правила розкладення арктангенса в нескінченний степеневий ряд. В Європі до таких результатів дійшли лише в 17 – 18 століттях.

8. Життєвий шлях і творчість Сринивази Ромамуджана

Срініваса Айєнґар Рамануджан (Srīnivāsa Aiyangār Rāmānujan, таміл. 22 грудня 1887 — 26 квітня 1920) — індійський математик, відомий своїм самородним талантом, що дозволив йому зробити значний внесок у математику (математичний аналіз, теорію чисел, теоріючислових рядів та теорію неперервних дробів), здобувши свої знання в основному самоосвітою.

Рамануджан народився і виріс в Ероде, Таміл-Наду, Індія. З математикою він уперше познайомився у десятирічному віці. З огляду на природну здібність учителі дали йому книгу з вищої тригонометрії, яку він опанував до 13 років, навіть відкривши свої власні теореми. До 17 років Рамануджан уже провів дослідження чисел Бернуллі та сталої Ейлера-Маскероні. Завдяки успіхам у математиці він отримав стипендію для навчання в урядовому коледжі в Кумбаконані, але не зумів туди поступити, проваливши екзамени з інших дисциплін. Він поступив до іншого коледжу, працюючи клерком в офісі головного бухгалтера Мадраського портового тресту. В 1912–1913 роках він послав приклади доведених теорем трьом науковцям із Кембриджу. Серед них тількиҐодфрі Гарольд Гарді (Hardy G.H.) зрозумів геніальність його робіт і запросив Рамануджана до Кембриджу для співпраці. Рамануджан швидко став членомЛондонського королівського товариства, але незабаром помер у віці всього 32 роки від хвороб, недоїдання та, можливо, печінкової інфекції.

За своє коротке життя Рамануджан незалежно від інших отримав 3900 математичних результатів, здебільшого тотожностей та рівнянь. Невелика кількість цих результатів виявилася помилковою, деякі були вже відомі, але правильність більшості з них була підтверджена. Його результати були оригінальними і дуже незвичними, відкрили простір для подальших досліджень.

На його честь названо астероїд 4130 Рамануджан.

9. Квадратні рівняння в Індії

Квадратні рівняння вирішували і в Індії. Завдання на квадратні рівняння зустрічаються вже в астрономічному трактаті «Аріабхаттіам», складеному в 499 році індійським математиком і астрономом Аріабхаттою. Інший індійський учений, Брахмагупта (VII століття), виклав загальне правило розв'язання квадратних рівнянь, приведених до єдиної канонічної форми:

a + bx = c, де a> 0.

У цьому рівнянні коефіцієнти, крім а, можуть бути і негативними. Правило Брахмагупти по суті збігається з нашим.

У Стародавній Індії були поширені публічні змагання в рішенні важких завдань. В одній із старовинних індійських книг йдеться з приводу таких змагань наступне: «Як сонце блиском своїм затьмарює зірки, так вчений чоловік затьмарить славу іншого в народних зборах, пропонуючи і вирішуючи алгебраїчні завдання». Завдання часто наділялися в віршовану форму. Різні рівняння як квадратні, так і рівняння вищих ступенів вирішувалися нашими далекими предками. Ці рівняння вирішували в самих різних і віддалених один від одного країнах. Потреба в рівняннях була велика. Рівняння застосовувалися в будівництві, у військових справах, і в побутових ситуаціях.

 Ось із завдань знаменитого індійського математика XII в.Бхаскари.

Завдання 13.

«На дві зграї розділившись,

Розважались в гаї мавпи.

Одна восьма їх в квадраті

Гучно разом збавлялись.

З криком радісним дванадцять

На ліанах колихали. 

Разом скільки, ти дізнайся,

Мавп було у тому гаї?»

Рішення Бхаскари свідчить у тому, що він теж знав про двозначності коренів квадратних рівнянь.

Відповідне завданню 13 рівняння:

 (x/8)² + 12 = x

Бхаскара пише у вигляді:

x² -64х = -768

і, щоб доповнити ліву частину цього рівняння до квадрата, додає до обох частин 32², одержуючи потім:

 

x² -64х + 32² = -768 + 1024,

(x - 32)² = 256,

x - 32 = ± 16,

x₁ = 16, x₂ = 48.

10. Математика сучасної  Індії. Міжнародні премії для індійських математиків

Субхаш Как (Нар. 26 березня 1947, Шрінагар, Кашмір)-Індія-американський вчений у галузі інформатики, завідувач кафедри інформатики Університету штату Оклахома. Найбільшу популярність здобув своїми індологіческой публікаціями з історії, філософії науки, давньої астрономії та історії математики. У галузі інформатики опублікував роботи по криптографії та квантової інформації.

Книги:

• Патанджали і когнітивної науки (1987);
• Індія на кінці століття , Південної Азії Книги / Голос Індії (1994);
• Древо бажання: Наявність і Обіцянка Індії (2001).

Дамодар Дхармананд Косамбі

(Скор. Д. Д. Косамби, англ. DD Kosambi; 31 липня 1907, Косбі, Гоа - 29 червня 1966, Бомбей, Індія) - індійський математик, статистик, філолог, історик марксистського толку і громадський діяч. Один з найвизначніших текстологів і фахівців з давньоіндійській літературі на санскриті, в галузі історії вивчав переважно древню Індію, її культуру і суспільні відносини.

З 1933 по 1945 Косамбі працював в коледжі ім. Фергюссона в Пуне, викладаючи математику і працюючи над теорією графів. У 1944 він видав невелику статтю на чотири сторінки, в якій виклав свою функцію карт.

У 1945 Бхабха Хоми Джехангир Баба запропонував Косамби посаду професора математики в Інституті фундаментальних досліджень (Інституті суспільних наук) ім. Тата в Бомбеї. Робота Косамби в Інституті ім. Тата (з 1945 до 1962) вважається найважливішим періодом його наукової діяльності.

Наваратна Шрініваса Раджарам

(Нар. 1943; Майсур, Британська Індія) - індійський математик, історик і лінгвіст, відомий своїми публікаціями з історії Стародавньої Індії, зокрема з теорії «корінних аріїв», яка є предметом великої полеміки в індійській політиці.

У 1970-х роках Раджарам отримав докторський ступінь з математики від Університету Індіани і опублікував ряд наукових праць за статистикою, а в 1980-х роках - по штучному інтелекту і робототехніки.

  Починаючи з 1984 року працював науковим консультантом для НАСА. Одночасно займався дослідженням зв'язку, що існує між ведичної математикою і математикою Стародавнього Єгипту та Вавілонії. З 1990-х років зайнявся вивченням наукової бази історії Стародавньої Індії.

Кальямпуді Радхакрішна Рао

(Нар. 10 вересня 1920, Хадаган) - найбільший індійський математик, статистик.

  Автор кількох теорем, пов'язаних зі статистичними оцінками параметрів розподілу.

З дитинства познайомився зі статистикою в індійському статистичному інституті, і вибрав цю область своєю майбутньою професією. Отримав ступінь магістра з математики в університеті Андхра та магістра за статистикою в університеті Калькутти в 1943 році.

Докторську дисертацію, написану під керівництвом Роберта Ейлмера Фішера і захищену в 1948 році, Рао присвятив дослідженням генів мишей.

Премії

Премія Неванлінни (або приз Неванлінни, англ. Rolf Nevanlinna Prize) - нагорода за видатні досягнення молодих математиків в галузі інформатики або обчислювальної математики. Присуджується раз на 4 роки на Міжнародному конгресі математиків. Засновано в 1981 році і названа в пам'ять ректора університету Хельсінкі і президента Міжнародного математичного союзу, фінського математика Рольфа Неванлінни, який помер роком раніше. Премія складається з грошового призу (10000 євро) і золотої медалі з профілем Неванлінни, на обідку якої викарбувано ім'я лауреата.

Премія Бальцана - міжнародна премія за вищі досягнення в науці і культурі, заснована дочкою італійця Еудженіо Бальцана (італ. Eugenio Balzan; 1874-1953), співвласника газети «Корр'єре делла Сера». Премія була присуджена в 1961-1962 роках і потім стала присуджуватися щорічно з 1978 року. Номінації премії змінюються, їх точний склад на наступний рік оголошується в травні. З 2001 року розмір становить 1 мільйон швейцарських франків, при цьому половину грошей лауреат зобов'язаний віддати молодим вченим, які зможуть фінансувати на отримані гроші свої проекти

 

3. Історію розвитку математики в Арабських країнах розглянемо за такими пунктами:

1.Математична школа «Дім знань» у Багдаді.

2.Аль Хорезміта його арифметичний трактат.

3.«Кiтаб аль-джебр аль-мукабала» Аль Хорезмі

4.Брати Бану Муса (Хст.).

5.Математичні здобутки Абу-л-Вафа.

6.Творчість Аль-Біруні.

7.Роботи Насират Тусі.

8.Математик і астроном Мухаммед Тарагай Улугбек (1394—1449 рр.).

9.Математичні здобутки Джамшида ал-Каши.

10.Омар Хайям – математик.

 

1.Математична школа «Дім знань» у Багдаді.

Початкові школи при мечетях існували з 8 століття. Вищі школи – мед сере були у Басрі, Куфі та Багдаді. Об’єднанню мусульман та поширення писемності сприяла арабська мова.

Багдадська школа: 8-9 ст. Вивчалася астрономія та математика. Найбільшою видатною спорудою був «Будинок мудрості» з бібліотекою та обсерваторією.

Перекладались та видавалися арабською з обширними коментарями твори: Евкліда, Архімеда, Апполонія, Менелая, Герона, Діофанта та ін. авторів.

2. Аль Хорезмі та його арифметичний трактат.

Аль Хорезмі великий узбецький математик, географ, історик та астроном. 813-833 рр. – очолив в Багдаді бібліотеку «Будинку мудрості», свого роду академії.

Вважається встановленим, що Аль-Хорезмі був автором 9 творів:

• Книга про індійську арифметику (або Книга про індійський рахунок);
• Коротка книга про числення алгебри і алмукабали;
• Астрономічні таблиці (зідж);
• Книга картини Землі;
• Книга про побудову астролябії;
• Книга про дії за допомогою астролябії;
• Книга про сонячний годинник;
• Трактат про визначення ери євреїв і їх свята;
• Книга історії.

З цих книг до нас дошли тільки 7 — у вигляді текстів або самого Аль-Хорезмі або його арабських коментаторів, або в перекладах налатину.

Книга алгебри Аль-Хорезмі (Китаб мухтасаб ал-джабр і ва-л-мукабала) складається з двох частин — теоретичної (теорія розв'язання лінійних і квадратних рівнянь, деякі питання геометрії) і практичної (застосування методів алгебри в розв'язанні господарський-побутових, торгових і юридичних завдань — ділення спадку, складаннязаповітів, розділ майна, різні операції, вимірювання земель, будівництво каналів). Слово ал-джабр (заповнення) означало перенесення негативного члена з однієї частини рівняння в іншу, і саме з цього терміну виникло сучасне слово «алгебра». Ал-мукабала (зіставлення) — скорочення рівних членів в обох частинах рівняння. Успадковане від східних математиків вчення про лінійні і квадратні рівняння стало основою розвитку алгебри в Європі.

3.«Кiтаб аль-джебр аль-мукабала» Аль Хорезмі

Кітаб аль-Джебр ва-ль-Мукабала (араб. الكتاب المختصر في حساب الجبر والمقابلة‎‎ — «Коротка книга доповнення і протиставлення» — відома книга арабського вченого Мухаммеда ібн Муси аль-Хорезмі, від назви якої походить термін «алгебра».

Книга ділиться на три частини:

• рівняння першої та другої ступені з вправами
• практична тригонометрія
• розв'язання задач за розподілом спадку

У рівняннях не використовуються символи, вони виражаються словами. Аль-Хорезмі виділяє наступні 6 типів рівнянь (a, b, c при цьому невід'ємні коефіцієнти; розглядаються тільки додатні розв'язки):

• «квадрати дорівнюють кореням» (ax² = bx)
• «квадрати дорівнюють числу» (ax² = c)
• «корені дорівнюють числу» (bx = c)
• «квадрати і корені дорівнюють числу» (ax² + bx = c)
• «квадрати і число дорівнюють кореням» (ax² + c = bx)
• «корені і число дорівнюють квадратам» (bx + c = ax²)

Кожен тип рівнянь розв'язується за правилом, яке доводиться геометрично.

4.Брати Бану Муса (Хст.).

Бану Муса (араб. بنو موسى) - сини Муси ібн Шакіра: Мухаммад, Ахмад і ал-Хасан - видатні вчені арабського Халіфату, що займалися геометрією, астрономією і механікою. Вони збирали рукописи грецьких авторів і побудували при «Домі мудрості» в Багдаді обсерваторію, в якій проводили спостереження в 850-870 роках. Ал-Біруні відзначає перевага їх астрономічних таблиць перед іншими, оскільки «вони не шкодували зусиль для досягнення істини і стояли в свою епоху самотньо за майстерністю і гостроті спостережень». Їх учнем був Сабіт ібн Куррі.

Братам належать обробка «Конічних перетинів» Аполлонія, «Книга вимірювання плоских і кульових фігур», «Книга про витягнутому колі» (тут описано побудову еліпса «способом садівника»), «Книга механіки», «Книга про рух першої сфери», «Книга про початок світу »,« Книга градусів про природу знаків зодіаку »,« Книга про побудову астролябії »та ін.

5.Математичні здобутки Абу-л-Вафа.

Абуль-Вафа Мухаммад ібн Мухаммад аль-Бузджані (араб. ابوالوفا البوزجانی, Бузган, 10 червня 940 - Багдад, 998) - один з найбільших математиків і астрономів середньовічного Сходу. Учитель Абу-л-Хасана ібн Юніса.

Абу-л-Вафа ввів тригонометричні функції тангенс і котангенс і побудував їх таблиці; знайшов з високою точністю значення синуса одного градуса. Він же вивів формулу для синуса суми двох кутів, і в один час з ал-Ходжанді і Ібн Іраком довів теорему синусів для сферичних трикутників:
 

Абу-л-Вафа склав коментарі до математичних працям ал-Хорезмі, Евкліда, Діофанту, Гиппарха. Йому належать книги «Про те, чого слід навчитися до вивчення арифметики», «Про те, що потрібно знати переписувачам, ділкам і іншим в науці арифметики», «Про те, що необхідно реміснику з геометричних побудов», «Про застосування шестидесятеричной таблиць» , «Про визначення ребра куба, квадрато-квадрата і того, що складається з них обох».

6.Творчість Аль-Біруні.

Твори Біруні є значним внеском у математику, астрономію, фізику, мінералогію, історію та етнографію. Біруні описав календарні системи арабів, персів, греків, євреїв, хорезмійців та інших народів. Автор фундаментальної праці про Індію. Загалом, Аль-Біруні залишив 152 наукових дослідження. З цієї величезної спадщини до нас дійшло лише 30. У низці трактатів Біруні виклав основи математики й астрономії. Вперше на Середньому Сході висловив думку про рух Землі навколо Сонця. Обчислив довжину кола Землі. Визначив питому вагу багатьох мінералів.

Розробив астрономічні методи геодезичних вимірювань. Удосконалив основні астрономічні інструменти, якими користувалися у той час (астролябію, квадрант, секстант), розвинув теорію тіней - гномоніку. Побудував перший нерухомий (стінний) квадрант радіусом 7,5 м для точних (до 2') спостережень Сонця і планет, який протягом 400 років був найбільшим у світі. Проведені ним вимірювання нахилу екліптики до екватора протягом багатьох століть залишалися неперевершеними за точністю.

Одним з перших після старогрецьких учених почав розвивати і широко застосовувати плоску і сферичну тригонометрію як математичну основу практичної астрономії. Розробив новий, вельми точний метод визначення радіусу Землі шляхом спостереження положення горизонту з вершини гори. За 600 років до Віллеброрда Снелліуса запропонував тригонометричний метод вимірювання відстаней, схожий з сучасною тріангуляцією.

7.Роботи Насир ат Тусі.

Насир ад-Дін Абу Джафар Мухаммад ібн Мухаммад Туси (перс. محمد بن محمد بن الحسن الطوسی, Тус, 18 лютого 1201 - Марага, 26 червня 1274) - перський [1] [2] [3] [4] [5] [6] [7] [8] математик, механік і астроном XIII століття [9], учень Камал ад-Діна ібн Юніса, надзвичайно різнобічний учений, автор творів з філософії, географії, музиці, оптиці, медицині, мінералогії.

Серед математичних праць Туси особливо значний «Трактат про повний четирехсторонніке» (в іншому перекладі - «Трактат про фігуру січних»). Трактат був написаний по-перському під час перебування ат-Тусі в Аламута і по-арабськи, в дещо скороченому вигляді, в Мараге (1260). В якості свого основного попередника ат-Тусі вказує на ал-Біруні з його «Книгою ключів науки астрономії про те, що відбувається на поверхні сфери». У трактаті згадується трактат ас-Салар з цього ж питання, причому в перської версії шанобливо, а в арабській - принизливо, що, мабуть, було пов'язано з боротьбою ат-Тусі проти ас-Салар при дворі Хулагу. Твір ат-Тусі стало одним із джерел для Региомонтана (1436-1476), з ім'ям якого пов'язаний початок нового етапу в історії тригонометрії.

Трактат ат-Тусі складається з п'яти книг. У I книзі викладена теорія складових відносин. Розвиваючи ідеї Сабіта ібн Коррі і Омара Хайяма, ат-Тусі вводить тут розширене поняття числа, яке визначається як відношення, раціональне або ірраціональне. У II книзі даються докази різних випадків теореми Менелая для плоского чотирикутника. У III книзі вводяться поняття синуса і косинуса дуги і доводиться ряд теорем плоскою тригонометрії; зокрема, тут розглядаються правила вирішення плоских трикутників і дано доказ плоскою теореми синусів. Книга IV присвячена доказу різних випадків теореми Менелая для сферичної фігури січних. У V книзі розглядаються прийоми вирішення завдань сферичної тригонометрії за допомогою теорем, «замінюють фігуру січних», - теореми тангенсов і теореми синусів. У заключній главі V книги пропонуються правила вирішення сферичних трикутників, причому для того випадку, коли в трикутнику дано три кути, вводиться поняття полярного трикутника.

8.Математик і астроном Мухаммед Тарагай Улугбек (1394—1449 рр.).

Мухаммед Тарагай ібн Шахрух ібн Тимур Улугбек гураган (перс. میرزا محمد طارق بن شاهرخ; 22 березня 1394, Сольтаніе - 27 жовтня 1449, Самарканд) - правитель тюркської держави Тимуридів, син Шахруха, онук Тамерлана. Відомий як видатний математик, астроном і астролог свого часу, також цікавився історією та поезією. Заснував одну з найважливіших обсерваторій середньовіччя.

Головним науковою працею Улугбека по праву вважаються «зідж джадид Гурагані» або «Нові Гураганови астрономічні таблиці». Автор завершив цей твір в 1444 році після тридцяти років кропіткої роботи та астрономічних спостережень. Астрономічний довідник незабаром був переведений на латинську мову і поряд з «Альмагест» Клавдія Птолемея і астрономічними таблицями кастильського короля Альфонса X був посібником з астрономії у всіх обсерваторіях Європи

9.Математичні здобутки Джамшида ал-Каши.

Гіяс-ад-дін Джамшид ібн Масуд аль-Каші (перс. غیاثالدین جمشید کاشانی, англ. Ghiyāth al-Dīn Jamshīd ibn Mas'ūd al-Kāshī; 1380, Кашан (Іран) - 22 червня 1429) - один з найбільших математиків і астрономів XV століття, співробітник Улугбека, один з керівників Самаркандської обсерваторії. Опублікував перше систематичний виклад теорії десяткових дробів.

У трактаті «Ключ арифметики» ал-Каші описує шістдесяткова систему числення. (В астрономічних трактатах стародавніх греків в Шістдесяткова системі записувалася тільки дрібна частина числа, а ціла частина записувалася в традиційній буквеної ионической системі. Ал-Каші запропонував записувати в Шістдесяткова системі і цілу частину теж. Тим самим він фактично повернувся до тієї форми запису, яка була в ходу у древніх вавилонян; але він сам навряд чи про це знав.) У цьому ж трактаті ал-Каші вводить десяткові дроби, формулює основні правила дії з ними і призводить способи перекладу шестидесятеричной дробів у десяткові і назад.

У «Трактаті про окружності» ал-Каші обчислює довжину кола за рецептом Архімеда - як середнє арифметичне між периметрами вписаного і описаного правильних багатокутників з числом сторін 3 · 228. Це дало йому для 2π наближення 6,2831853071795865. Це значення, вірне у всіх 16 десяткових знаках, було отримано з обчисленого ним раніше в Шістдесяткова системі значення з 9 знаками. Цим він поставив рекорд, що протримався до 1596 року, коли Людольф ван Цейла обчислив число π з 35 десятковими знаками. Крім того, напевно можна сказати, що ця робота ал-Каші була першим історично зафіксованим прикладом переведення дробу з однієї системи числення в іншу.

10.Омар Хайям – математик.

Омар Хайям — перський поет, математик та філософ — народився 18 травня 1048 року і помер 4 грудня 1131 року.

Повне його ім’я — Гіяс ед-Дін Абу-ль-Фатх Омар ібн Ібрахім ель-Хайямі ен-Найсабурі.

У Ісфахані, при дворі Малік-шаха, Омар Хайям продовжив заняття математикою. Відомі математичні результати, досягнені Хайямом, відносять до трьох напрямків: до алгебри, до теорії паралельних та до теорії відношень і вченню про число.

Алгебраїчні твори Омара Хайяма — їх збереглося до наших днів два (третій, без назви, не знайдений) — містили теоретичні висновки надзвичайної важливості. У своєму знаменитому “Трактаті про доведення задач алгебри та алмукабали”, вперше в історії математичних дисциплін, Хайям дав повну класифікацію усіх видів рівнянь — лінійних, квадратних і кубічних (всього 25 видів) і розробив систематичну теорію рішення кубічних рівнянь за допомогою властивостей конічних перерізів.

Книги Омара Хайяма довгий час залишалися невідомими європейським вченим, творцям нової вищої алгебри, і вони були змушені пройти довгий і нелегкий шлях, що за 5-6 століть до них уже проклав Омар Хайям. Так, з подібним твердженням виступив Р.Декарт у 1637 році, а ще 200 років потому, у 1837 році, це було доведено П. Ванцелем.

Ще одна математична праця Хайяма — “Труднощі в арифметиці” — був присвячений методу знаходження коренів будь-якого ступеня з цілих чисел; в основі цього методу Хайяма лежала формула, що пізніше одержала назву бінома Ньютона. Цей трактат не знайдений, але його згадував сам Хайям у “Трактаті про доведення задач алгебри та алмукабали”.

 

ІV.  Підведення підсумків