Паралельні прямі. Кути, що утворені при перетині двох прямих січною. Ознаки паралельності прямих

Тема. Паралельні прямі. Кути, що утворені при перетині двох прямих січною. Ознаки паралельності прямих

Мета: домогтися засвоєння учнями змісту понять: паралельні прямі, січна, відповідні кути та ознаки паралельності прямих (за відповідними кутами); виробити вміння формулювати означення паралельних прямих та ознаку паралельних прямих, зображувати на рисунку пара­лельні прямі, січну, а також відповідні кути при двох паралельних прямих та січній, розв'язувати однокрокові задачі на доведення паралельності прямих.

Тип уроку: засвоєння знань і вмінь.

Обладнання: набір демонстраційного креслярського приладдя, таб­лиця № 7 «Паралельні прямі».

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання    

Самостійна робота № 4

Варіант 1

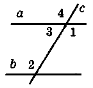
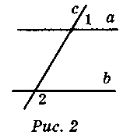
Довести, що а || b, якщо:
a) 1 = 2 (рис.  1);   б) 1 + 2 = 180° (рис.  2).

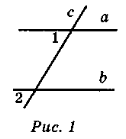
Варіант 2

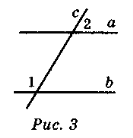
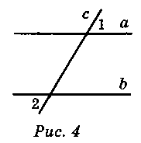
Довести, що а || b, якщо:
a) 1 + 2 = 180° (рис. 3);  б) 1 = 2 (рис. 4).

III. Формулювання мети і завдань уроку. Мотивація навчальної діяльності  учнів    

Методичний   коментар

Для мотивації навчальної діяльності учнів доречно буде звернутися до демонстраційних таблиць, що стисло відобра­жають зміст вивченого матеріалу, та запропонувати учням ус­тановити логіку вивченого матеріалу.

Складений спільними зусиллями учнів та вчителя логічний ланцюжок може бути таким (див. схему № 4).

Схема № 4

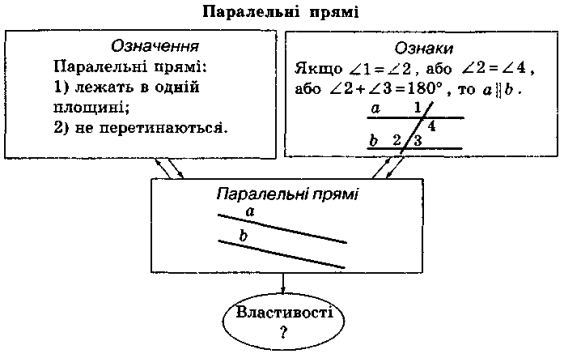
Тепер буде логічним перейти до питання про інший випадок (окрім випадку перетину двох прямих) взаємного розміщення двох прямих на площині. Після проведеного обговорення вчи­тель формулює погоджену з учнями мету уроку.

IV. Актуалізація опорних знань і вмінь учнів   

Усні   вправи

1. З-поміж фігур, зображених на рис. 37, виберіть ті, що вважаються основними в планіметрії.

2. За  рис.   38  сформулюйте  основні  властивості  вивчених геометричних фігур.

V. Засвоєння нових знань    

План вивчення нового матеріалу

1. Уявлення про випадки взаємного розміщення двох пря­мих на площині.
2. Означення паралельних прямих.
3. Поняття січної; кути, утворені при перетині двох прямих січною; відповідні кути.
4. Ознака паралельних прямих за відповідними кутами.

Методичний   коментар

Поняття паралельних прямих не є новим для семикласників, оскільки воно відоме їм з шостого класу, так само учням на інтуїтивному рівні відома аксіома паралельних. Тому на дано­му уроці необхідно систематизувати знання учнів про взаємне розміщення двох прямих на площині та їх властивості, виокре­мивши випадок паралельних прямих; сформулювати означен­ня та ознаки паралельних прямих, сформувавши попередньо уявлення про внутрішні різносторонні кути, як одні з таких, що утворюються при перетині двох прямих січною. (Звернімо увагу на той факт, що в даному підручнику не змінено підхід до викладення цього питання: основною вважається ознака за внутрішніми різносторонніми кутами, а ознака паралельності за внутрішніми односторонніми кутами та за відповідними кутами вважається висновком з основної ознаки.)

У будь-якому разі при вивченні цього матеріалу доречно буде звернутись до наочності (див. таблицю № 7 «Паралельні прямі»).

Таблиця № 7

Паралельні прямі

VI. Первинне усвідомлення нових знань

Усні   вправи

1. Відомо, що  а || b. Чи означає це, що  b || a?
2. Два відрізки не мають спільних точок. Чи означає це, що відрізки обов'язково паралельні?
3. Прямі KM і EF паралельні. Чи можуть промені МК і FE перетинатися?
4. На площині проведено три паралельні прямі. Чи може деяка четверта пряма:

а) перетинати тільки одну з даних прямих;

б) перетинати тільки дві з даних прямих;

в) не перетинати жодної з даних прямих?

5. Чи можна провести два промені з початком у точці поза даною прямою, які були би паралельні даній прямій? Якими мають бути ці промені?
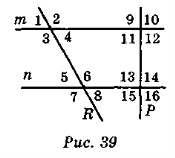
6. На рис. 39 назвіть прямі, що перетнуті січними; січні; пари відповідних кутів при прямих m i n i січній k; при прямих m i n i січній р.

Графічні   вправи

За допомогою двосторонньої лінійки проведіть паралельні прямі а і b.

1. Позначте на прямій а точку А. Чи можна провести через точку А іншу пряму, паралельну прямій b? чому?
2. Побудуйте відрізок AD, паралельний прямій b. Чи ле­жить точка D на прямій а?
3. Проведіть через точку А пряму с, що не пристає до прямої а. Чи перетинаються прямі b і с? чому?
4. Проведіть пряму l, що є січною прямих а і b; позначте на рисунку і запишіть пари відповідних кутів.

Письмові вправи: № 171, 173 (б), 183.

VII. Підсумки уроку    

Запитання   до   учнів

1. Прямі т і n не мають жодної спільної точки. Що можна сказати про прямі т і п?
2. Точка С не лежить на прямій п. Скільки прямих, па­ралельних прямій п, можна провести через точку С? Скільки прямих, паралельних прямій п, можна провес­ти?

VIII. Домашнє завдання    

1. § 5, 6, с. 40, 47—49 — вивчити означення та ознаки.
2. Письмово: № 172,  174 (а),  175,  182 (а, б).
3. Додаткова задача. На площині проведено чотири прямі, причому три з них мають одну спільну точку. Скільки пар паралельних прямих можуть при цьому утворитися? Розгляньте всі можливі випадки.