Перетворення графіків тригонометричних функцій

ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ САМОСТІЙНОЇ РОБОТИ

Тема:  Перетворення графіків тригонометричних функцій. Гармонічні коливання.

Мета:    Виробити практичні навички побудови і перетворення графіків тригонометричних функцій. Визначення періоду тригонометричної функції. Визначення амплітуди, фази та періоду гармонічних коливань.

Контрольні запитання:

1. Яку функцію називають періодичною?
2. Назвіть область визначення і область значень кожної з тригонометричних функцій.
3. Назвіть найменший період кожної з тригонометричних функцій.
4. Як називаються графіки тригонометричних функцій?
5. Назвіть нулі усіх тригонометричних функцій.
6. Назвіть проміжки знакосталості усіх тригонометричних функцій.
7. Назвіть проміжки монотонності усіх тригонометричних функцій.
8. Що таке коливання? Яке коливання називають гармонічним?
9. Якими можуть бути амплітуда, період та початкова фаза гармонічного коливання?
10. Чи можна стверджувати, що графік функції y=tg x зростає на всій області визначення?
11. Розкажіть алгоритм побудови графіка функції  у=asinbx, у=acos(bx+c).
12. Розкажіть алгоритм побудови графіка функції  у=asin(bx+c)+d, у=tg(x+c)+d.

Література:

1. Бевз Г.П., Бевз В.Г Математика 10.Рівень стандарту. – К.: Генеза, 2011 р.

Розділ 2, §14 стор.109–114, §15 стор.117–121. 

2. Афанасьєва О.М., Бродський Я.С. Математика. – К.: Вища школа, 2001 р.

Розділ ІІ, §1(1.4–1.6) стор. 68–80. 

3. М.І.Шкіль Алгебра і початки аналізу 10 кл. – Київ “Зодіак-ЕКО”, 2002 р.

Розділ 1, §6 стор.50–56, 64–65.

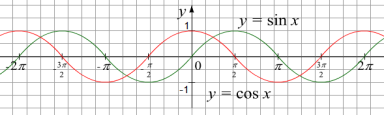
Приклад 1.

Побудова графіка функції y=cos x може бути виконана за допомогою геометричних перетворень графіка функції y=sinx, використовуючи формулу зведення :

Приклад 2. Розглянемо приклад побудови графіка функції:

Скористаємося графіком функції у=соs x. Паралельно перенесемо його вздовж осі Ох на відстань праворуч і отримаємо графік функції

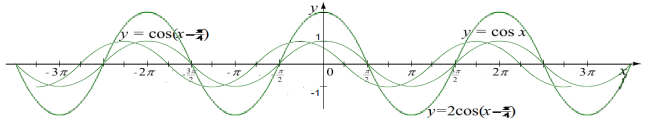Ординату кожної точки цього графіка збільшимо вдвічі. Отримаємо шуканий графік:

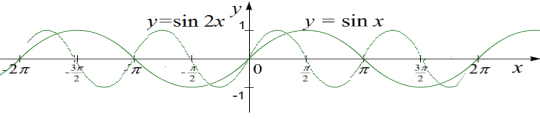
Приклад 3. Розглянемо приклад побудови графіка функції:

Скористаємося графіком функції у=sin x.

Період даної функції Т=, тому наш графік стискається вздовж осі Ох вдвічі:

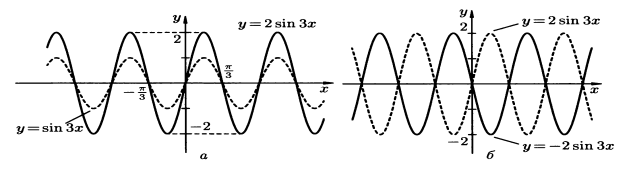
Приклад 4 Розглянемо приклад побудови графіка функції:

Скористаємося графіком функції у=sin x.

Період даної функції Т=, тому наш графік стискається вздовж осі Ох втричі:

Приклад 5. Розглянемо приклад побудови графіка функції:

Приклад 6.

Визначити амплітуду, фазу, початкову фазу, період  і кутову швидкість гармонічного коливання, заданого формулою:

Розв’язування: Оскільки формула гармонічного коливання має вигляд , маємо:

 амплітуда А=3,  фаза – , початкова фаза –- , кутова швидкість =4, період Т=.

Критерії оцінювання:

Робота містить 4 завдання: №№1-3 по 3 бали, №3 – 2 бали

Бали за виконання завдань №№1-2 відповідно виставляються :

  а) за правильну побудову графіка і записи відповідних перетворень (3бали);

б) за правильну побудову графіка без запису відповідних перетворень (2 бали);

в) за частково правильну побудову графіка або запис необхідних перетворень (1 бал);

г) у решті випадків 0 балів.

Бали за виконання завдань №№4 відповідно виставляються :

  а) за правильну відповідь і записи без помилок  (2 бали);

б) за правильну відповідь і записи з помилками або за часткове розв’язування, яке не доведене до відповіді (1 бал);

в) у решті випадків 0 балів.

Завдання для самостійного виконання: