Тестові роботи з геометрії (стереометрії) для 10 класу Запропоновані тестові завдання можуть бути використані з метою організації та проведення тестової перевірки знань учнів з гео

Тестові роботи з геометрії (стереометрії) для 10 класу

Запропоновані тестові завдання можуть бути використані з метою організації та проведення тестової перевірки знань учнів з геометрії за наступними темами:

1. Паралельність прямих та площин.
2. Перпендикулярність прямих та площин.

Роботи розроблено у 3 – 4 варіантах, різнорівневі.

І рівень – репродуктивного характеру. Вимагає знання визначень, теорем, ознак, формул.

ІІ рівень – складається з більш складних задач, вимагає більш широкого круга математичних знань, вмінь та практичних навичок.

ІІІ рівень – складається із задач рівня підвищеної складності, розв’язок яких потребує творчого застосування набутих знань.

До кожного завдання І та ІІ рівнів запропоновано варіанти відповідей, один з яких є правильним. На допомогу вчителеві наведено таблиці відповідей до кожного тесту та  критерії оцінювання.

 

Тест № 1

(у чотирьох варіантах)

Тема: Паралельність прямих та площин.

І рівень  4 завдання   1б∙4=4б

ІІ рівень  2 завдання   2б∙2=4б

ІІІ рівень  3 завдання   3б∙3=9б

    Всього 17 балів

 

Оцінювання

від 0б до 7б  «1-3 бали»

від 8б до 11б  «4-6 балів»

від 12б до 15б «7-9 балів»

від 16б до 17б «10-12 балів»

 

Таблиця відповідей на завдання тестової роботи № 1

варіант	І рівень				ІІ рівень		ІІІ рівень
	1	2	3	4	1	2	1	2	3
І вар.	Г	Г	Б	Б	Б	В	Паралельні	4 см	32 см
ІІ вар.	Б	В	В	Г	В	Б	Паралелограм	4 см	41 та 57 см
ІІІ вар.	В	Б	В	Б	Г	В	Мимобіжні	9 см	78 см
IV вар.	А	Б	Г	Б	В	В	Рівні	2 см	27 см

 

 

 

ТЕМА : Паралельність прямих та площин

Тест № 1

І ВАРІАНТ

І рівень

1. Скільки площин можна провести через три точки, які не лежать на одній прямій?

а) безліч ;   б) дві;    в) жодної ; г) одну;      д) три.

 

2. Дано паралельні прямі a і b. Скільки існує площин, які проходять через пряму a та паралельні до прямої b?

а) жодної;      б) одна;      в) дві;      г) безліч;     д) три.

 

3. Трикутник побудовано у площині α, яка паралельна до площини β. Як розміщено сторони цього трикутника відносно площини β?

а) перетинають площину;     б) паралельні до площини;     в) належать площині.

 

4. Як розміщено площини α і β, якщо пряма a перетинає площину α та паралельна до площини β?

а) паралельні;      б) перетинаються ;     в) співпадають.

 

ІІ рівень

1. Чотири точки не належать одній площині. Яка найбільша кількість точок належать одній прямій?

а)  жодної;       б) дві;    в) три;     г) одна;     д) чотири.

2. Кут між мимобіжними прямими дорівнює φ. Вказати неправильне значення кута φ.

а)  φ=30^о;    б) φ=90^о;        в) φ=0^о;      г)  φ=45^о;       д) φ=20^о. 

 

ІІІ рівень

1. Чотири точки А, В, С, D не належать одній площині. Через середини відрізків АВ та ВС, АD та DС проведено прямі. Яким може бути взаємне розміщення цих прямих?

 

2. Відрізок АВ не перетинає площину. Через кінці відрізка АВ проведено паралельні прямі, які перетинають площину у точках А₁ та В₁. Через точку С, яка ділить відрізок АВ у співвідношенні АС:СВ = 1:2, також проведено пряму, яка паралельна до прямих АА₁ та ВВ₁. Знайдіть довжину відрізка СС₁, якщо АА₁ = 2 см та ВВ₁=8 см.

 

3. Через вершини паралелограма проведено паралельні прямі до перетину з площиною, яка не має з ним спільних точок. Довжини відрізків цих прямих, від трьох послідовних вершин паралелограма до площини дорівнюють відповідно 27,44 та 49 см. Обчисліть довжину відрізка від четвертої вершини паралелограма до цієї площини.

 

 

 

ТЕМА : Паралельність прямих та площин

Тест № 1

ІІ ВАРІАНТ

І рівень

1. Дано прямі a і b, паралельні до прямої с. Яке взаємне розміщення прямих a і b?

а) перетинаються; б) паралельні; в)мимобіжні.

 

2. Дано мимобіжні прямі a і b. Скільки існує площин, які проходять через пряму a та паралельні до прямої b?

а) дві;      б) жодної;      в) одна;      г) безліч;     д) три.

 

3. Скільки площин, паралельних до заданої площини, можна провести через точку поза даної площини?

а) дві; б) безліч;      в) одну;       г) три;       д) жодної.

 

4. Пряма а паралельна до площини α. Скільки площин, паралельних до площини α, можна провести через задану пряму?

а) дві;      б) жодної;      в) безліч;      г) одну;      д) три.

 

ІІ рівень

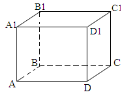
1. На малюнку зображено куб АВСDА₁В₁С₁D₁. Яке взаємне розміщення прямих А₁В₁ та DС?

а) мимобіжні;        б) перетинаються;        в) паралельні.

 

2. Прямі АВ та СD перетинаються. Яке твердження вірне?

а) прямі АС та ВD   б) прямі АС та ВD   в) прямі АС та ВD

можуть перетинатися;  можуть бути мимобіжними            можуть бути

паралельними

 

ІІІ рівень

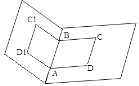
1. Паралелограми АВСD та А₁В₁С₁D₁  належать різним площинам. Який вид має чотирикутник СDD₁С₁?

 

 

2. Через кінець А відрізка АВ проведено площину. Через кінець В і точку С цього відрізка проведено паралельні прямі, які перетинають цю площину у точках В₁ та С₁. Знайдіть довжину відрізка АВ, якщо ВВ₁=6 см, АС:СС₁ = 2:3?

 

3. Через вершини паралелограма та точку перетину його діагоналей  проведено паралельні прямі до перетину з площиною, яка не має з паралелограмом спільних точок. Довжини відрізків цих прямих від двох суміжних вершин та точки перетину діагоналей паралелограма до площини відповідно дорівнюють 61, 45 та 51 см. Обчисліть довжини відрізків від двох інших вершин паралелограма до цієї площини.

 

 

 

ТЕМА : Паралельність прямих та площин

Тест № 1

ІІІ ВАРІАНТ

І рівень

1. Укажіть малюнок, на якому зображено мимобіжні прямі?

а)             ;   б)          в)

 

 

2. Укажіть неправильне твердження

а)Через точку, яка не належить заданій прямій, можна провести пряму, паралельну до цієї прямої, причому тільки одну

б) Якщо пряма у просторі перетинає одну з двох паралельних прямих, то вона обов’язково перетинає й другу

в) Якщо дві різні площини мають спільну точку, то вони перетинають-ся по прямій

г) Якщо дві точки прямої належать заданій площині, то вся пряма належить цій площині

 

3. Паралельні прямі  a, b і с не належать одній площині. Пряма d перетинає прямі a і b. Яке взаємне розміщення прямих d і с?

а) перетинаються;     б) паралельні;     в) мимобіжні;         г) співпадають.

 

4. Площини α і β паралельні. Пряма a перетинає площину α. Як розміщення пряма відносно до площини β?

а) паралельна до площини;        б) перетинає площину;        в) належить площині.

 

ІІ рівень

1. Прямі a, b і с попарно перетинаються. Скільки площин можна провести через ці прямі?

а)  нескінчену кількість;       б) дві;    в) жодної;     г) одну;     д) три.

 

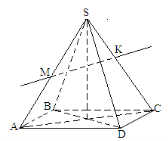2. На малюнку зображено чотирикутну піраміду SABCD. Через середини ребер  SA та SC проведено пряму MK. Яке твердження вірне?

а)  прямі МК та CD перетинаються;    

б) Прямі МК та ВС паралельні;       

в) пряма МК паралельна до площини грані АВCD;     

г) прямі МК та Ас перетинаються. 

 

ІІІ рівень

1. Прямі  АВ та СD мимобіжні. Яке взаємне розміщення прямих АС і ВD?

 

2. Площина паралельна до сторони АВ трикутника АВС та перетинає сторону АС у точці А₁, а сторону ВС у точці В₁.Знайдіть довжину відрізка А₁В₁,якщо           АВ = 24см та АА₁ : А₁С = 5:3.

 

3. Через вершини правильного трикутника та його центр проведено паралельні прямі до перетину з площиною, яка не має з трикутником спільних точок. Довжини відрізків цих прямих від двох вершин трикутника та його центра до площини дорівнюють 31, 41 та 50 см відповідно. Обчисліть довжину відрізка від третьої вершини трикутника до цієї площини

ТЕМА : Паралельність прямих та площин

Тест № 1

ІV ВАРІАНТ

І рівень

3. Через три точки проведено дві різні площини. Як розміщено і точки?

а) лежать на одній прямій; б) належать одній прямій.

 

4. Дві прямі не паралельні та не перетинаються. Скільки площин можна провести через ці прямі?

а) дві;      б) жодної;      в) одну;      г) безліч;     д) три.

 

3. Дві прямі перетинаються. Скільки площин можна провести через ці прямі?

а) жодної;         б) дві;           в) безліч;       г) одну;       д) три.

 

4. Прямі a і b не перетинаються. Яке взаємне розміщення цих прямих, якщо пряма a паралельна до площини, а пряма b перетинає цю площину?

а) паралельні;      б) мимобіжні.

 

ІІ рівень

1. Сторона АВ паралелограма АВСD належить площині α, а сторона СD не належить їй. Як розміщена пряма СD відносно площини α?

а) перетинає  площину;        б) належить площині;     в) паралельна до площини

2. На малюнку зображено куб АВСDА₁В₁С₁D₁. Знайти кут між площинами АСDС₁А₁ та ВDD₁.

а)  45^о;    б) 30^о;        в) 90^о;      г)  120^о;       д) 60^о. 

 

 

ІІІ рівень

1. Чотири точки А, В, С, D не належать одній площині. Точки Мі N – середини відрізків AB та BC, а точки  P і K – середини відрізків AD та DC. Порівняйте відрізки MN та PK?

 

2. Відрізок  АВ перетинає  площину. Через кінці відрізка АВ та його середину М проведено паралельні прямі, які перетинають площину у точках А₁ , В₁  та М₁ . Знайдіть довжину відрізка  ММ₁, якщо АА₁=3 см,  ВВ₁=7 см.

 

3. Через вершини  правильного трикутника та його центр проведено паралельні прямі до перетину з площиною, яка не має з трикутником спільних точок. Довжини відрізків цих прямих від вершин трикутника до площини відповідно дорівнюють 19, 27 та 35 см. Обчисліть довжину відрізка від центру трикутника до цієї площини.

 

 

Тест № 2

(у трьох варіантах)

Тема: Перпендикулярність прямих та площин.

І рівень  1 завдання   1б∙1=1б

ІІ рівень  3 завдання   2б∙3=6б

ІІІ рівень  3 завдання   3б∙3=9б

    Всього 17 балів

 

Оцінювання

від 0б до 6б  «1-3 бали»

від 7б до 10б  «4-6 балів»

від 11б до 14б «7-9 балів»

від 15б до 16б «10-12 балів»

 

Таблиця відповідей на завдання тестової роботи № 2

варіант	І рівень	ІІ рівень			ІІІ рівень
	1	1	2	3	1	2	3
І вар.	Б	В	Г	В	13	7	6 та 15
ІІ вар.	В	Г	А	В	2	13
ІІІ вар.	Б	В	Б	Б	16π	10	8

 

 

 

ТЕМА : Перпендикулярність прямих та площин

Тест № 2

І ВАРІАНТ

І рівень

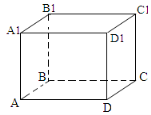
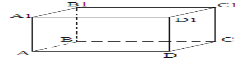1. На малюнку зображено прямокутний паралелепіпед ABCDA₁B₁C₁D₁ . Довжина якого відрізка є відстанню між мимобіжними прямими AD та A₁B₁?

а) A₁D;     б) АА₁;        в) DB₁;         г) A₁D₁.

 

 

ІІ рівень

1. Відстань від точки М до всіх сторін квадрату дорівнює 13 см. Знайдіть відстань від точки М до площини квадрата, якщо сторона квадрата дорівнює 10 см.

а) 8 см;        б) 11 см;     в) 12 см;      г) 14 см;        д) 15 см

 

2. Відстань від точки до двох перпендикулярних площин дорівнює 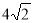см. Знайдіть відстань від цієї точки до прямої перетину цих площин

а)  6 см;            б) 4,5 см;        в) 3 см;            г)  8 см;       д) 4 см.

 

3. Із заданої точки до площини проведено перпендикуляр та похилу. Довжина перпендикуляра дорівнює проекції похилої, Знайти кут між перпендикуляром та похилою.

а)  30^о;    б) 60^о;        в) 45^о;      г)  40^о;       д) 20^о.

 

ІІІ рівень

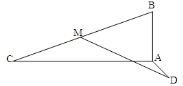
1. Відрізки  АВ, АС та АD попарно перпендикулярні. Точка М – середина відрізка ВС. Знайти довжину відрізка DМ, якщо АВ = 6 см, АС = 8 см, АD = 12 см.

 

 

2. Із вершини рівностороннього трикутника АСВ до його площини проведено перпендикуляр АD. Знайти відстань від точки D до сторони ВС трикутника, якщо АD=1 см, ВС=8 см.

 

3. З точки до площини проведено дві похилі довжиною 10 та 17 см відповідно. Різниця проекцій цих похилих дорівнює 9 см. Знайдіть проекції похилих.

 

 

 

ТЕМА : Перпендикулярність прямих та площин

Тест № 2

ІІ ВАРІАНТ

 

І рівень

1. Прямі a і b перпендикулярні до площини. Яке взаємне розміщення цих прямих?

а) перетинаються;     б) мимобіжні;        в) паралельні.

 

ІІ рівень

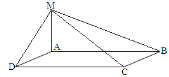
1. Відрізок АМ проведено перпендикулярно до площини прямокутника АВСD. Який відрізок має більшу довжину?

а) МА;        б) МD;     в) МВ;      г) МС;        д) АD.

 

2. Із центра кола проведено перпендикуляр до ї площини. Знайти діаметр кола, якщо довжина перпендикуляра 4 см, а відстань від його кінця до очок кола 5 см.

а)  6 см;            б) 3 см;        в) см;            г)  см;       д) -.

 

3. Відстань від точки до площини дорівнює16 см. Знайти довжину похилої, якщо вона утворює з площиною кут 30^о.

а)  25 см;           б) 30 см;        в) 32 см;         г)  35 см;       д) 55 см.

 

ІІІ рівень

1. Точка М знаходиться на відстані 4 см від вершин рівностороннього трикутника зі стороною 6 см. Знайти відтань від точки М до площини трикутника.

 

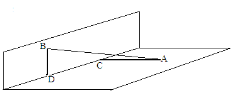2. Із точок А і В, які належать двом перпендикулярним площинам, проведено перпендикуляри АС та ВD на пряму перетину площин. Знайти довжину відрізка АВ, якщо        АС = 3 см, ВD = 4 см, СD = 12 см

 

3. З точки, яка віддалена від площини на 2 см, проведено дві похилі, які утворюють з площиною кути 45^о і 30^о,  а між собою прямий кут. Знайдіть відстань між основами похилих.

 

 

ТЕМА : Перпендикулярність прямих та площин

Тест № 2

ІІІ ВАРІАНТ

 

І рівень

1. Площина перпендикулярна до однієї з двох паралельних прямих. Як розміщена друга пряма відносно до цієї площини?

а) паралельна до площини;     б) перпендикулярна до площини;       

в) належить площині.

 

ІІ рівень

1. Знайти відстань від вершини А куба АВСDА₁В₁С₁D₁ до площини  ВDD₁В₁, якщо сторона куба дорівнює 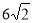 см.

а) 7 см;        б) 4 см;     в) 6 см      г) 10 см.

 

 

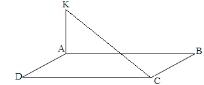2. Із вершини А квадрата АВСD до його площини проведено перпендикуляр АК довжиною 6 см. Знайти відстань від точки К до вершини С квадрата, якщо його сторона дорівнює 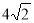см

а)  9 см;            б) 10 см;        в) 10,5см;           

г)  12 см;       д) 14 см.

 

3. Кінці відрізка, який не перетинає площину, віддалені від неї на 3 см та 5 см. Знайти відстань від середини відрізка до площини..

а)  2 см;           б) 4 см;        в) 6 см;         г)  8 см;       д) 12 см.

 

ІІІ рівень

1. З центра кола проведено перпендикуляр до його площини. Знайти довжину кола, якщо довжина перпендикуляра 6 см, а відстань від кінця цього перпендикуляра, який не належить площині, до точок кола 10 см.

 

2. Із вершини прямого кута С рівнобедреного прямокутного трикутника АСВ проведено перпендикуляр СD до площини цього трикутника, Знайти відстань від точки D до його гіпотенузи, якщо СD = 8 см, АВ = 12 см.

 

3. З точки, яка віддалена від площини на 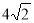 см, проведено дві похилі, які утворюють з площиною кути 45^о,  а між собою – кут 60^о  . Знайдіть відстань між основами похилих.