Тема уроку. Перпендикуляр і похила. Взаємозв'язок між довжинами похилих, проведених з однієї точки, і довжинами їх проекцій.

Мета уроку: формування понять: перпендикуляр до площини, похила, основа похилої, основа перпендикуляра, проекції похилої на площину, відстань від точки до площини. Виявлення взаємозв'язку між довжинами двох похилих, проведених з однієї точки до площини, і довжинами їх проекцій.

Обладнання: стереометричний набір.

Хід уроку

І. Перевірка домашнього завдання

1. Два учні відтворюють на дошці розв'язання задач № 14, 15.

2. Розв'язування задач.

1) Дано площину α, перпендикулярну до неї пряму а і іншу пря­му b, яка не лежить в площині α. Укажіть, які з наведених твер­джень правильні, а які — неправильні:

а) якщо b || a, то b α;

б) якщо b α , то b || а ;

в) якщо b α, то а і b мимобіжні;

г) якщо b α, то а і b перетинаються.

2) Дано площину α, паралельну їй пряму а і деяку пряму b, яка не лежить в площині α. Укажіть, які з наведених тверджень пра­вильні, а які — неправильні:

а) якщо b || a, то обов'язково b || α;

б) якщо b α, то обов'язково b а;

в) якщо b α і b перетинає а, то b а;

г) якщо b α, то b і а обов'язково мимобіжні.

3. Обговорення правильності виконання учнями задач № 14, 15.

II. Сприйняття й усвідомлення нового матеріалу

Перпендикуляр і похилі, взаємозв'язок між довжинами похилих. проведених з однієї точки, і довжинами їх проекцій

Перпендикуляром, опущеним з даної точки на дану площину, називають відрізок прямої, перпендикулярної до площини, що міс­титься між даною точкою і площиною.

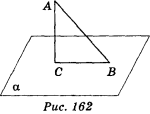На рис. 162 пряма AC перпендикулярна до площини α і перетинає її в точці С, отже, відрізок AC — перпендикуляр, опущений з точки А на площину α. Кінець цього відріз­ка, який лежить у площині, тобто точка С, називається основою перпендикуляра.

Якщо AC — перпендикуляр до площини α, а точка В — відмінна від С точка цієї пло­щини, то відрізок АВ називають похилою, про­веденою з точки А на площину α. Точка В — основа похилої. Відрізок, що з'єднує основи перпендикуляра і похилої, проведених з однієї і тієї самої точки, називається проекцією похилої. На рис. 162 відрізок ВС — проекція похилої АВ на площину α.

Прикладами матеріальних моделей перпендикулярів є: стовпи, теле­візійні вежі тощо.

Розв'язування задач

1. Знайти довжину похилої, якщо довжина перпендикуляра дорівнює 4 см, а проекція похилої на площину — 3 см.
2. Знайти проекцію похилої на площину, якщо похила дорівнює 13 см, а перпендикуляр, проведений з тієї ж точки,— 12 см.
3. Знайти довжину перпендикуляра, якщо похила дорівнює 10 см, а її проекція на площину — 8 см.
4. Скільки перпендикулярів можна опустити з даної точки до даної площини? Чому?
5. Скільки похилих можна провести з даної точки до даної площини?
6. Як слід установити на хрестовині ялинку, щоб вона була перпенди­кулярна до площини підлоги?
7. Як на практиці за допомогою виска перевірити вертикальність встановленого стовпа?

Слід зазначити, що перпендикуляр, опущений з точки, корот­ший за будь-яку похилу, проведену через дану точку.

Відстанню від точки до площини називається довжина пер­пендикуляра, опущеного з цієї точки на площину.

Розв'язування задач

1. Знайти відстань від точки А до граней куба, якщо ребро куба дорів­нює 10 см (рис. 163).

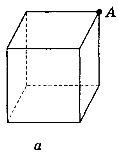
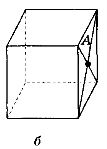
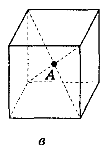
Рис. 163

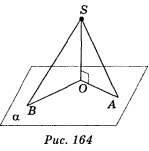2. Із точки S проведено до площини а перпендикуляр SO та похилі SA і SB. Довжини похилих відповідно дорівнюють 13 і 20 см. Дов­жина проекції похилої AS дорівнює 5 см (рис. 164). Знайти від­стань від точки S до площини та довжину проекції похилої SB.

Вивчення взаємозв'язку між довжинами похилих, проведених з однієї точки, і довжинами їх проекції доречно провести шляхом розв'язування задач.

Задача.

Із деякої точки проведено до площини дві похилі і перпендикуляр. Доведіть, що якщо:

1) похилі рівні, то рівні і їх проекції;

2) проекції похилих рівні, то рівні і похилі.

3) похилі нерівні, то більша похила має більшу проекцію.

Доведення

Нехай АВ α (рис. 165); AC і AD — похилі; AC > BD .

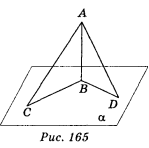Із ΔAСВ AC = .

Із ΔАDB  AD = .

Згідно з умовою AC > AD , тоді

> ;

АВ² + ВС² > АВ² + BD², або ВС² > BD²; отже, ВС > BD . 4) Доведіть: якщо похилі нерівні, то більшій проекції відповідає біль­ша похила.

III. Закріплення та осмислення знань учнів

Розв'язування задач

1. Задача № 22 із підручника (с. 36).

2. Задача № 23 із підручника (с. 36).

Розв'язання

Нехай АВ α (рис. 165); AC = 17 cm, AD = 10 cm, СB – BD = 9 cm. Нехай BD = x cm, тоді CB = (x + 9) cm.

Із ΔАВD: АВ² = AD² – BD² = 100 – x².

Із ΔАСВ: АВ² = AC² – BC² = 289 – (x+ 9)². Тоді 100 – x² = 289 – (x + 9)²; 100 – x² = 289 – x² – 18x – 81; 18x = 108; x = 6.

Отже, BD = 6 cm, CB = 6 + 9 = 15 (см).

Відповідь. 6 см і 15 см.

3. Задача № 25 із підручника (с. 36).

Розв'язання

Нехай АВ α (рис. 165); AD = 23 см, AC = 33 см, BD : CB = 2 : 3.

Нехай BD = 2x см, CB = 3х см. Із ΔАВD: АВ² = AD² – BD² = 23² - 4x².

Із ΔАВС: АВ² = AC² – BC² = 33² – 9x². Тоді 23² – 4x² = 33² – 9x²;

5x² =33² – 23²; 5x² = (33 – 23)(33 + 23);  x² =112 і АВ = =

= = = 9 (см). Отже, довжина перпендикуляра дорів­нює 9 см.

Відповідь. 9 см.

IV. Домашнє завдання

§ 3, п. 18; контрольні запитання № 7—9; задача № 24 (с. 36).

V. Підведення підсумку уроку

Запитання до класу

1. Що таке перпендикуляр, опущений з даної точки до площини?
2. Що таке похила, проведена з даної точки до площини?
3. Скільки перпендикулярів та похилих можна побудувати з даної точки до площини?
4. 3 даної точки до площини проведено дві похилі. Що можна стверджу­вати про проекції похилих на площину, якщо похилі:

а) рівні;             б) не рівні?