Тема уроку.   Розв'язування задач на відстань від прямої до паралельної їй

                        площини .

Мета уроку: формування вмінь учнів застосовувати властивості точки, рівновіддаленої від вершин многокутника, та знань про відстань від прямої до паралельної їй площини, відстань між паралельними площинами до розв'язування задач.

Обладнання: стереометричний набір.

Хід уроку

І. Перевірка домашнього завдання.

1. Два учні відтворюють розв'язування задач .№ 17, 19 на дошці.

2. Математичний диктант.

З центра правильного:

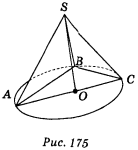
варіант 1 — трикутника (рис. 175);

варіант 2 — чотирикутника (рис. 176)

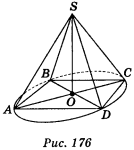проведено перпендикуляр SO до площини АВС, SO = 1 см, АВ = 1 см.

 Користуючись зображенням, знайдіть:

1) проекцію похилої SA на площину АВС; (2 бали)

2) відрізки, які дорівнюють відрізку ОА; (2 бали)

3) похилі, що дорівнюють похилій SA; (2 бали)

4) довжину похилої SA; (2 бали)

5) кут між похилою SA і перпендикуляром SO; (2 бали)

6) висоту трикутника SAB, проведену з вершини S. (2 бали)

Відповідь.

Варіант 1. 1) см; 2) 0В, ОС; 3) SB, SC; 4) см; 5) arctg=30⁰; 6) см.

Варіант 2. 1)см; 2) OB, ОС, OD; 3) SB, SC, SD; 4)см; 5) arctg; 6) см.

3. Обговорення правильності виконання учнями задач на дошці.

II. Закріплення та осмислення знань учнів

Розв'язування задач

1. У рівнобедреному трикутнику кут при вершині дорівнює 120°, а біч­ні сторони — по 10 см. Поза площиною трикутника дано точку, яка віддалена від кожної із вершин на 26 см. Знайдіть відстань від цієї точки до площини трикутника. (Відповідь. 24 см.)
2. У трикутнику АВС <A = 45°, ВС = 12 см. Точка S знаходиться від його площини на відстані 6 см і на однаковій відстані від кожної вершини трикутника. Знайдіть відстань від точки S до вершин трикутника.  (Відповідь. 6 см.)
3. Трапеція вписана в коло, причому менша основа, яка дорівнює 16 см, стягує дугу 60°. На відстані 12 см від площини трапеції зна­ходиться точка, рівновіддалена від кожної її вершини. Знайдіть відстань від цієї точки до вершини трапеції. (Відповідь. 20 см.)

III. Сприйняття й усвідомлення нового матеріалу

Поняття відстані від прямої до паралельної їй площини

Відстанню від прямої до паралельної їй площини називається відстань від будь-якої точки цієї прямої до площини.

Розв'язування задач.

1. Задача № 26 із підручника (с. 36).

2. Задача № 28 із підручника (с. 36).

Розв'язання

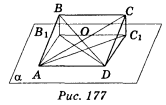
Нехай ABCD — ромб; ВВ₁ α; СС₁ α; AD α; ВВ₁ = СС₁ = 4 м, B₁D = 2 м, АС₁ = 8 м (рис. 177). Оскільки AD || ВС; ВС || В₁C₁; AD = ВС = В₁С₁, то AB₁C₁D — паралелограм.

Із ΔВВ₁D : BD = = = 2(см).

Із ΔАСС₁: АС = = = 4 (см).

Із ΔАОВ АВ = = = = 5 (см).

Із ΔАВВ₁ АВ₁ = = = = 3 (см).

Відповідь. 3 см і 5 см.

Поняття відстані між паралельними площинами

Відстанню між паралельними, площинами називається відстань від будь-якої точки однієї площини до другої площини.

Розв'язування задач

1. Задача № 30 із підручника (с. 36).

2. Задача № 32 із підручника (с. 36).

Розв'язання

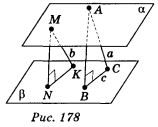
Нехай α || β; А α, М α, С β, К β; АВ β; MN β ; АС = а,        МК = b, ВС = с (рис. 178).

Із ΔАВС AB = = . Оскільки АВ = MN,

то із ΔMNK:  NK === = .

Відповідь. .

IV. Домашнє завдання

Підготуватися до тематичної атестації № 3 та розв'язати зада­чі № 27, 31 (с. 36).

V. Підведення підсумку уроку

Запитання до класу

1) Що розуміють під відстанню між прямою і паралельною їй площиною?

2) Знайдіть відстань від прямої а до площини АВС, якщо ребро куба дорівнює  6 см (рис. 179).

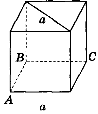
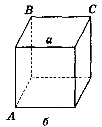
Рис. 179

3) Що називається відстанню між паралельними площинами?

4) Дано зображення куба ABCDА₁B₁С₁D₁. Ребро куба дорівнює 10 см. Знайдіть відстань між площинами: а) АВС і А₁В₁С₁; б) А₁АВ і D₁DC .