Тема уроку.  Властивість точки, рівновіддаленої від вершин многокутнику.

Мета уроку: формування знань про властивість точки, рівновіддаленої від вершин многокутника, та вмінь застосовувати цю властивість до розв'язування задач.

Обладнання: стереометричний набір, схема «Коло, описане навколо многокутника».

Хід уроку

І. Перевірка домашнього завдання

1. Перевірити розв'язання задачі № 24 за записами (з пропусками), зробленими на дошці до початку уроку.

Розв'язання задачі № 24 Нехай АВ α (рис. 166).

1) ВС = 40 см, BD =...; нехай AD = х см, тоді АС=.... Із ΔАВD: АВ² = х² –12² = х² – 144. Із ΔАВС АВ².... Тоді х² – 144 = (х + 26)² – 40²; 52х=...; х =15. Отже, AD=..., AC = 41 см.

2) BD=..., BC=7 см; нехай АD=...,тоді AC = 2х см.

Із ΔАВD AB²=.... Із ΔАВС АВ² = 4х² – 49.

Тоді х² – 1 = ...; 3х² = ...; х² = 16. Звідси х = ...; отже, AD =..., AC = 2·4 = 8 (см).

Відповідь. 1) 15 см і 41 см; 2) 4 см і 8 см.

2. Математичний диктант.

МО — перпендикуляр до площини ОАВ; <AOB = 90° (рис. 167); МА і MB — похилі.

Варіант 1 — МО = 1 см, ОА = 3 см, MB = см;

варіант 2 — МО = 1 см, ОВ = 4 см, МА = см. Користуючись зображенням, знайдіть:

1) довжину невідомої похилої; (2 бали)

2) довжину невідомої проекції похилої; (2 бали)

3) довжину відрізка АВ; (2 бали)

4) відстань від точки О до середини відрізка АВ; (2 бали)

5) відстань від точки М до середини відрізка АВ; (2 бали)

6) відстань від точки А до площини МОВ. (2 бали)

Відповідь. Варіант 1.1) см; 2) см; 3) см; 4) см; 5) см; 6) 3 см.

        Варіант 2. 1) см; 2) 3 см; 3) 5 см; 4) 2,5 см; 5) см; 6) 3 см.

II. Сприйняття й усвідомлення нового матеріалу

Властивість точки, рівновіддаленої від вершини многокутника

Теорема 1.

Якщо через центр кола, описаного навколо многокутника, проведено пряму, перпендикулярну до площини многокут­ника, то кожна точка цієї прямої рівновіддалена від вер­шин многокутника.

Доведення

Нехай ABCD — чотирикутник, навколо якого описане коло з центром у

точці О, і OS(ABC). Доведемо, що SA = SB = SC = SD (рис. 168).

ΔASO = ΔBSO = ΔCSO = ΔDSO (за двома катетами: SO — спільний,

АО = BO = CO = DO ).

Із рівності трикутників випливає, що SA = SB = SC = SD.

Теорема 2.

Якщо деяка точка рівновіддалена від вершин многокутни­ка, то основа перпендикуляра, опущеного з даної точки на площину многокутника, збігається з центром кола, опи­саного навколо многокутника.

Доведення

Нехай ABCD — даний чотирикутник, для точки S простору SA = SB = SC = SD і SO АВС . Доведемо, що точка О — центр кола, описаного навколо ABCD (рис. 168). ΔASO = ΔBSО = ΔCSO = ΔDSO (за гіпотенузою і катетом: SO — спільний, AS = BS = CS = DS — за умо­вою). Із рівності трикутників випливає, що АО = BO = CO = DO , тобто точка О — центр кола, описаного навколо чотирикутника ABCD.

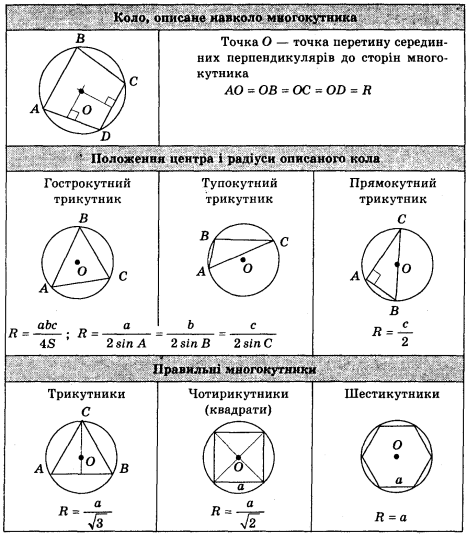
Далі слід нагадати формули для знаходження радіуса кола, описано­го навколо деяких многокутників, за допомогою даної стінної таблиці.

Розв'язування задач

1. <ABC = 90°; МА = MB = МС (рис. 169). Опустіть з точки М перпендикуляр на площину АВС.

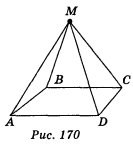
2. ABCD — квадрат, АВ = 4 см, МА = MB = MC = MD = 5 см (рис. 170). Знайдіть відстань від точки М до площини АВС.

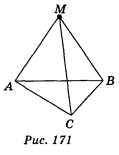
3. АВ = ВС = АС = 5 см; МА = MB = MC = 13 см (рис. 171). Знай­діть відстань від точки М до площини АВС.

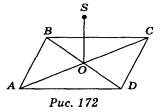
4. ABCD — квадрат, SO (ABC), SO = 2см, АВ = 4 см (рис. 172). Знайдіть відстань від точки S до вершин квадрата.

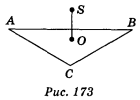
5. ΔАВС – правильний; точка О – центр трикутника; АВ = 3см; SO(АВС); SO = см (рис. 173). Знайдіть відстань від точки 5 до вершин трикутника АВС.

6. Задача 21 із підручника (с. 35).

7. Задача 20* із підручника (с. 35).

III. Домашнє завдання

Задачі № 6, 17—19 (с. 34—35).

IV. Підведення підсумку уроку

Запитання до класу

1. Яку властивість мають точки, які лежать на перпендикулярі, про­веденому до площини многокутника через центр кола, описаного навколо многокутника?
2. Де знаходяться точки, рівновіддалені від вершин деякого много­кутника?
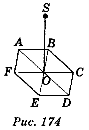
3. Через центр О правильного шестикутника ABCDEF проведемо перпендикуляр SO до площини АВС (рис. 174). Укажіть, які з поданих тверджень пра­вильні, а які — неправильні:

а) відстані від точки S до вершин шестикутника ABCDEF різні;

б) кут OAS дорівнює куту OCS;

в) якщо ОА = 1 cm, SO = 1 см, то SA = cm;

г) якщо SO = OB, то <OSB = 60°.

4. Відстані від точки S до всіх вершин прямокутника ABCD однакові, точка О — точка перетину діагоналей АС і BD прямокутника ABCD. Укажіть, які з поданих тверджень правильні, а які — не­правильні:

а) пряма SO перпендикулярна до прямої АС;

б) пряма SO не перпендикулярна до прямої BD;

в) пряма SO перпендикулярна до площини АВС;

г) якщо АВ = 6 см, ВС == 8 см і AS = 13 см, то SO = 12 см.