Тема уроку.   Відстань від точки до прямої. Розв'язування задач на застосування теореми про три перпендикуляри.

Мета уроку: формування вмінь учнів застосувати теорему про три перпендикуляри до розв'язування задач, знаходження відстані від точки до прямої.

Обладнання: стереометричний набір.

Хід уроку

І. Перевірка домашнього завдання.

1. Два учні відтворюють на дошці розв'язування задач № 13, 41.

2. Математичний диктант.

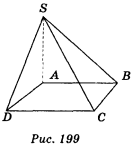
ABCD — прямокутник (рис. 199), SA(ABC).

Варіант 1 — SA = см, АВ = 1 cm, AD = 3 см;

варіант 2 — SA = см, АВ = 1 см, AD = 2 см.

Користуючись зображенням, знайдіть:

1) довжину відрізка SB; (2 бали)

2) довжину діагоналі АС; (2 бали)

3) довжину відрізка SD; (2 бали)

4) величину кута SBC; (2 бали)

5) величину кута SDC; (2 бали)

6) площу трикутника SDC. (2 бали)

Відповідь. Варіант 1. 1) 2 см; 2) см; 3) 2см; 4) 90°; 5) 90°; 6) см². Варіант 2. 1) см; 2) см; 3) см; 4) 90°; 5) 90°; 6) см².

3. Обговорення результатів диктанту та розв'язання задач на дошці.

II. Сприйняття й усвідомлення нового матеріалу

Поняття про відстань від точки до прямої

Нехай задані в просторі пряма а і точка А, що не лежить на даній прямій (рис. 200).

Відстанню від точки А до прямої а називаєть­ся довжина перпендикуляра, опущеного з точки А на пряму а. На рис. 200 ОА — відстань від точки А до прямої а.

Розв'язування задач

1. З точки М опустити перпендикуляр на пряму АВ (рис. 201).

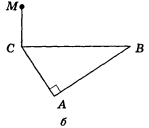
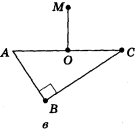
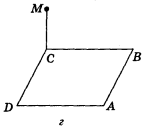
Рис. 201.

а) МС(АВС), АС = ВС ;         б) МС(АВС), <BAC = 90° .

в) МО(АВС), АО = ОС, <ABC = 90°; г) ABCD — квадрат, MC(ABC).             

2. Через точку О перетину діагоналей квадрата ABCD проведено до його площини перпендикуляр МО довжиною 15 см. Знайдіть відстань від точки М до сторін квадрата, якщо його сторона дорівнює 16 см. (Відповідь. 17 см.)
3. Відрізок AS, що дорівнює 12 см, перпендикулярний до площини трикутника АВС, в якому АВ = АС = 20 см, ВС = 24 см. Знайдіть відстань від точки S до прямої ВС. (Відповідь. 20 см.)
4. До площини прямокутника ABCD, площа якого дорівнює 180 см², проведено перпендикуляр SD, SD = 12 см, ВС = 20 см. Знайдіть відстань від точки S до сторін прямокутника. (Відповідь. 12 см; 12 см; 15 см; 4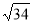см.)
5. Катет AC прямокутного трикутника дорівнює а, кут В дорівнює φ. Через вершину прямого кута проведено до площини цього трикут­ника перпендикуляр МС довжиною а. Знайдіть відстань від кінців перпендикуляра до гіпотенузи. (Відповідь. a cos φ; a .)
6. У трикутнику АВС сторони АВ = 13 см, ВС = 14 см, АС = 15 см. Із вершини А проведено до його площини перпендикуляр AD дов­жиною 5 см. Знайдіть відстань від точки D до сторони ВС. (Відповідь. 13 см.)
7. До площини ромба ABCD, у якого <A = 45°, АВ = 8 см, проведено перпендикуляр МС довжиною 7 см. Знайдіть відстань від точки М до сторін ромба. (Відповідь. 7 см; 7 см; 9 см; 9 см.)

8. Задача № 51* із підручника (с. 38).

III. Домашнє завдання

Повторити п. 19 із § 3; задачі № 42; 48, 53 (с. 37—38).

IV. Підведення підсумку уроку

Запитання до класу

1. Що називається відстанню від точки до прямої?
2. Знайдіть відстань від точки А до прямої а, якщо ребро куба дорів­нює 2 см (див. с 142 рис. 202).

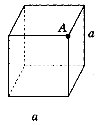
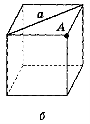
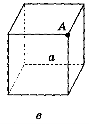
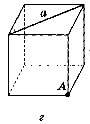
Рис. 202

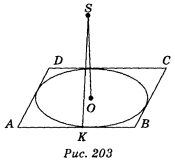3. Із центра О кола, вписаного в ромб ABCD, проведено перпендику­ляр SO до площини ромба. Коло дотикається до сторони АВ ромба у точці К, кут DAB — тупий (див. с 142 рис. 203). Укажіть, які з наведених тверджень правильні, а які — неправильні:

а) OK AB ;

б) проекцією відрізка SK на площину ромба є відрізок OS;

в) SK OK ;

г) довжина відрізка SK дорівнює від­стані від точки S до будь-якої сторони ромба.