Тема уроку. Перпендикулярні площини. Ознака перпендикулярності площин.

Мета уроку: формування поняття перпендикулярності площин. Вивчення ознаки перпендикулярності площин.

Обладнання: стереометричний набір, моделі куба і прямокутного паралелепіпеда.

Хід уроку

І. Перевірка домашнього завдання

1. Перевірити виконання задач № 49, 50 за записами, зробленими до початку уроку на дошці.

Розв'язання задачі № 49

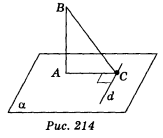
Нехай ABα; А α, d α; АВ = b, AC d, AC = a (рис. 214). За теоремою про три перпендикуляри ВС d , отже, ВС — відстань від точки В до прямої d. Із ΔАВС ВС = =  .

Відповідь. .

Розв'язання задачі № 50

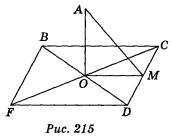
Нехай FBQD — квадрат (рис. 215). Оскільки точка А рівновіддалена від сто­рін квадрата, то основа перпендикуляра АО точка О (АО(АВС)) є центром кола, вписаного в квадрат FBCD, тобто точка О — точка перетину діагоналей квадрата. Проведемо ОМCD, тоді AMCD, AM = a. FC = BD = d.

Із ΔFCD FD = FC · cos45° = d · = . Тоді ОМ = FD = .

Із ΔАОМ  AO = = = .

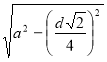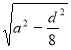Відповідь. .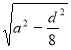

2. Самостійна робота.

Варіант 1

Периметр правильного трикутника дорівнює 36 см, а відстані від деякої точки до кожної із сторін трикутника — 10 см. Знайти відстань від цієї точки до площини трикутника.

Варіант 2

Площа правильного трикутника дорівнює 108 см². Точка відда­лена від площини трикутника на 8 см і рівновіддалена від його сторін. Знайти відстані від цієї точки до сторін трикутника.

Варіант З

Сторони трикутника дорівнюють 13, 14 і 15 см. Точка простору від­далена від кожної сторони цього трикутника на 5 см. Знайти відстань від цієї точки до площини трикутника.

Варіант 4

Сторони трикутника дорівнюють 36, 25 і 29 см. Відстань від деякої точки до площини трикутника дорівнює 15 см. Відстані від цієї точки до сторін трикутника рівні. Знайдіть ці відстані.

Відповідь. Варіант 1. 8 см. Варіант 2. 10 см. Варіант 3.3см. Варіант 4.17 см.

II. Сприйняття й усвідомлення нового матеріалу

Поняття перпендикулярних площин

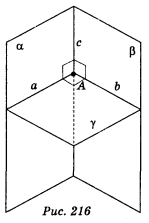
Дві площини, що перетинаються, нази­ваються перпендикулярними, якщо тре­тя площина, проведена перпендикуляр­но до лінії перетину цих площин, пере­тинає їх по перпендикулярних прямих. На рис. 216 α β, бо площини α і β пере­тинаються по прямій с, площина γ, перпенди­кулярна до с, перетинає α і β по прямих а і b, які перпендикулярні.

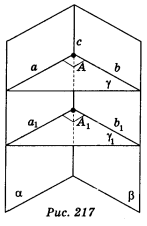Означення перпендикулярності площин не залежить від вибору площини γ. Дійсно, візь­мемо іншу площину γ₁, перпендикулярну до прямої с (рис. 217).

Оскільки с γ та прямі a і b лежать у пло­щині γ і перетинаються в точці А, то с а, с b (за означенням перпендикулярності пря­мої і площини).

Аналогічно с а₁, с b₁. Крім того, а і а₁b, b і b₁ лежать відповідно в площинах α і β. Отже, а || а₁ і b || b₁. Оскільки а b , а || a₁ і b || b₁, то а₁ b₁ (теорема 3.1).

Розв'язування задач

1. Наведіть приклади моделей перпендику­лярних площин із оточення.

2. Покажіть на моделі прямокутного паралеле­піпеда перпендикулярні грані (площини).

3. Дано зображення куба ABCDA₁B₁C₁D₁. Ука­жіть площини, які перпендикулярні до пло­щини:

а) АВС;   б) ADC₁;  в) АСС₁.

4. На двох перпендикулярних площинах вибрали по прямій. Чи може статися, що ці прямі:

а) паралельні; б) перетинаються; в) мимобіжні?

Відповідь проілюструйте прикладами з оточення.

5. Задача № 59 (1, 3, 5) із підручника (с. 39).

Ознака перпендикулярності площин

Доведення ознаки перпендикулярності двох площин провести, як це зроблено в підручнику (§ 3, п. 20, теорема 3.6).

Подамо зразок запису теореми 3.6 на дошці і в зошитах.

Теорема.

Дано: а, b, b α, β, b β.

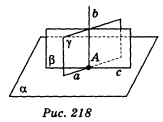
Довести: α β(рис. 218).

Доведення

Нехай α і β перетинаються по прямій с, а пряма c перетинається з b в точці А. Через точку А в площині α проведемо пряму а, а с. Через а і b прове­демо площину γ,  с а, с b, отже, γ с. Оскільки а b, то α β .

Розв'язування задач,

1. Як на практиці встановити, чи перпендикулярна площина стіни до площини підлоги?

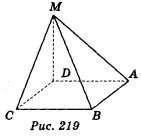
2. ABCD — квадрат, MD(АВС) (рис. 219). Доведіть, що:

а) (MAD) (MCD); б) (MBC) (MCD).

3. У трикутнику АВС <C = 90°; PB (ABC) (рис. 220). Доведіть, що (РАС) (РВС).

4. Задача № 54 із підручника (с. 38).

5. Чи правильні твердження:

а) через точку, взяту поза площиною, можна провести площину, перпен­дикулярну до цієї площини, і притому тільки одну;

б) якщо площина перпендикулярна до даної площини, то вона перпендикуля­рна і до довільної прямої, паралельної цій площині?

6. Задача № 55 із підручника (с. 38).

7. Задача № 61 із підручника (с. 39).

III. Домашнє завдання

§ 3, п. 20; контрольні запитання № 11, 12;

задачі № 59 (2; 4; 6), 60 (с. 39).

IV. Підведення підсумку уроку

Запитання до класу

1) Які площини називаються перпендикулярними?

2) Сформулюйте ознаку перпендикулярності площин.

3) Дано куб ABCDA₁B₁C₁D₁. Враховуючи, що ребра куба, які виходять з однієї вершини, попарно перпендикулярні, укажіть серед наведе­них тверджень правильні:

а) площини АD₁С і AD₁D перпендикулярні;

б) площини AD₁C і CDD₁ перпендикулярні;

в) площини AD₁C і ADC перпендикулярні;

г) площини ADD₁ і ADC перпендикулярні.

4) Дано дві перпендикулярні площини α і β та пряму с, яка перпен­дикулярна до площини α. Укажіть, які з наведених тверджень правильні, а які — неправильні:

а) пряма с обов'язково належить площині β;

б) пряма с може бути паралельною площині β;

в) якщо пряма с, належить площині β, то вона паралельна лінії пе­ретину площин α і β;

г) будь-яка площина, яка містить пряму с, перпендикулярна до площини α.