Тема уроку. Відстань між мимобіжними прямими.

Мета уроку: формування понять спільного перпендикуляра, відстані між мимобіжними прямими.

Обладнання: стереометричний набір.

Хід уроку

І. Перевірка домашнього завдання

1. Фронтальне опитування.

1) Які дві площини називаються перпендикулярними?

2) Сформулюйте ознаку перпендикулярності площин.

3) Як розташована пряма, яка лежить в одній із двох перпендику­лярних площин і перпендикулярна до лінії перетину цих площин, відносно другої площини?

4) Як розташована лінія перетину двох площин, які перпендикуля­рні, відносно третьої площини, що перетинає їх по перпендикуляр­них прямих.

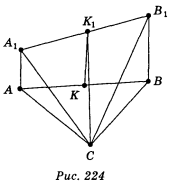2. Перевірити правильність виконання задачі № 56 за записами, зроб­леними на дошці перед уроком.

Задача № 56.

Дано:

АА₁(АВС); ВВ₁(АВС); АВ = ВС = АС = 2м, СА₁=3м, СВ₁ = 7 м; А₁К₁ = К₁В₁ (рис. 224).

Знайти: CK₁.

Розв'язання

1) Із ΔАА₁С АА₁ = = = (м).

2) Із ΔВВ₁С  ВВ₁ = = = 3 (м).

3) К₁К (АВС), К₁К = = = 2 (м).

4) Із ΔАСК  CK = = = (м).

5) Із ΔKK₁С СК₁ = = = (м).

Відповідь, м.

Запитання до класу

1) Чому трикутник АА₁С — прямокутний?

2) Чому трикутник ВВ₁С — прямокутний?

3) Визначте вид чотирикутника АА₁В. Чим буде відрізок KK₁ для чотирикутника АА₁В ? Як знайти довжину відрізка КК₁ ?

4) Як по-іншому можна було знайти довжину відрізка СК?

3. Самостійна робота.

Варіант 1

Відрізок довжиною 25 см опирається кінцями на дві взаємно перпен­дикулярні площини. Відстані від кінців відрізка до площини дорівню­ють 15 і 16 см. Знайдіть проекції відрізка на кожну площину.

Варіант 2

Відрізок довжиною 25 см опирається кінцями на дві взаємно перпен­дикулярні площини. Проекції відрізка на ці площини дорівнюють і 20 см. Знайдіть відстані від кінців відрізка до даних площин.

Варіант З

Кінці відрізка лежать у двох взаємно перпендикулярних площинах. Проекції відрізка на кожну із площин дорівнюють і 20 см відпо­відно. Відстань між основами перпендикулярів, проведених із кінців від­різка до площин, дорівнює 12 см. Знайдіть довжину даного відрізка.

Варіант 4

Із кінців відрізка, що лежать у двох взаємно перпендикулярних пло­щинах, проведено перпендикуляри до цих площин, довжини яких від­повідно дорівнюють 16 і 15 см. Відстань між основами цих перпендику­лярів дорівнює 12 см. Знайдіть довжину даного відрізка.

Відповідь.  Варіант 1. 20 см і 3 см.  Варіант 2. 15 см і 16 см.

Варіант 3. 25 см.    Варіант 4. 25 см.

II. Сприйняття й усвідомлення нового матеріалу

Систематизація відомостей про мимобіжні прямі

Запитання до класу

1) Як можуть розташовуватися дві прямі у просторі?

2) Які прямі називаються мимобіжними?

3) Як через одну з мимобіжних прямих провести площину, паралель­ну другій прямій?

4) Чи можна через дві мимобіжні прямі провести паралельні між собою площи­ни? Якщо так, то як це зробити? (Ви­конується побудова на дошці і в зоши­тах учнів (рис. 225)).

Якщо точка В — точка перетину пря­мих а₁ і b і АВ α , то яке взаємне розташування прямої АВ і прямих а і b?

Формування поняття спільного перпендикуляра

Спільним перпендикуляром до двох мимобіжних прямих на­зивається відрізок з кінцями на цих прямих, перпендикуля­рний до кожної з них.

Виконання вправ

1. Вкажіть дві мимобіжні прямі з оточення, а також спільний перпен­дикуляр до цих прямих.
2. Вкажіть спільні перпендикуляри до прямих АВ і CD на зображенні

куба (рис. 226, а, б, в).

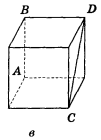
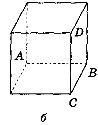
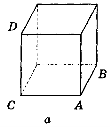
Рис. 226

Доведення єдиності спільного перпендикуляра до мимобіжних пря­мих а і b можна запропонувати учням розібрати за підручником само­стійно, а після цього відповісти на запитання:

1. Чому CD b' ?

2. Чому CD α?

3. Чому CD || АВ ?

4. Чому в площині, яка проходить через прямі АВ і CD, повинні ле­жати прямі а і b?

5. Чи можуть прямі а і Ь лежати в одній площині?

Виконання вправ

1. Побудуйте спільні перпендикуляри до прямих АВ і CD на зобра­женні куба (рис. 227).

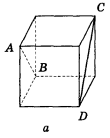
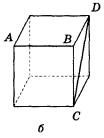
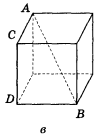
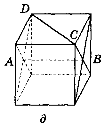
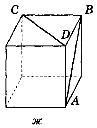
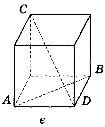
Рис. 227

2. Побудуйте спільний перпендикуляр до прямих:

1) АВ і SC; 2) AS і ВС; 3) AC і SB на зображенні тетраедра SABC, всі ребра якого рівні.

Формування поняття відстані між мимобіжними прямими та вмінь знаходити її

Відстанню між мимобіжними прямими називається довжина їх спільного перпендикуляра. Вона дорівнює відстані між паралельними площинами, які проходять через ці прямі.

Розв'язування задач

1. Ребро куба дорівнює 10 см. Яка відстань між прямими а і b (рис. 228)?

2. Кожне ребро тетраедра SABC дорівнює 10 см. Знайдіть відстань між прямими AS і ВС.

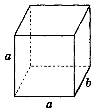
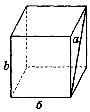
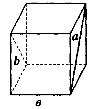
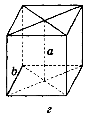
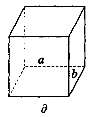
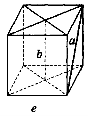
Рис. 228

III. Домашнє завдання

§ 3, п. 21; контрольні запитання № 13—15.

Розв'язати наступну задачу.

Ребро куба ABCDA₁B₁C₁D₁ дорівнює 2 см. Знайдіть відстань між пря­мими:

1. AD₁ і В₁С ; б) АВ і СС₁; в) АВ і B₁D.

IV. Підведення підсумку уроку

Запитання до класу

1. Що таке спільний перпендикуляр до мимобіжних прямих?
2. Сформулюйте властивості спільного перпендикуляра до мимобіж­них прямих.
3. Що таке відстань між мимобіжними прямими?
4. Чому дорівнює відстань між мимобіжними прямими?
5. Відстань між мимобіжними прямими а і b дорівнює 20 см. Через ці прямі проведено паралельні площини α і β так, що а лежить в α, a b лежить в β. Укажіть, які з наведених тверджень правильні, а які — неправильні:

1) довжина спільного перпендикуляра прямих а і b дорівнює 10 см;

2) відстань між площинами α і β дорівнює 20 см;

3) відстань між прямою а і площиною р дорівнює 15 см;

4) довжина відрізка з кінцями на прямих а і b може дорівнювати 22 см.