Тема уроку. Розв'язування задач на застосування ознаки перпендикулярності площин.

Мета уроку: формування вмінь учнів застосовувати означення та ознаку перпендикулярності площин до розв'язування задач.

Обладнання: стереометричний набір.

Хід уроку

І. Перевірка домашнього завдання

Фронтальна бесіда за контрольними запитаннями № 11—12 та пе­ревірка виконання задач № 59 (2; 4; 6), 60.

Розв'язання задачі № 59 (напівусне)

Перпендикулярні площини α і β перетинаються по прямій т, точ­ка А належить площині α, точка В — площині β. Точки А і В не лежать на прямій m. Із точок А і В проведено перпендикуляри AD і ВС до пря­мої m, причому точки С і D лежать на прямій т і не збігаються. Ука­жіть, які з наведених тверджень правильні, а які — неправильні:

а) АС β;

б) трикутник BCD — прямокутний;

в) АВ² = AD² – CD² + СВ²;

г) якщо АС = 1 см, ВС = 2 см, то АВ = cm.

Відповідь. см.

II. Закріплення та осмислення знань учнів

Розв'язування задач

1. Задача № 58* (с. 39).

Розв'язання

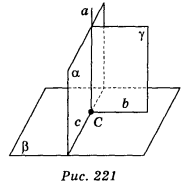
Нехай α β, α і β перетинаються по прямій с, а α, a с. Дове­демо, що α β (рис. 221). Прямі а і с перетинаються в точці С. Проведе­мо в площині β через точку С пряму b с. Через прямі а і b проводимо площину γ, с а (за умовою), b с (за побудовою), тому с γ, α β, отже, а b (за означенням перпендикулярних площин),        а b, а с отже, а β.

2. Задача.

Якщо дві площини, що перетинаються, перпендикулярні до тре­тьої площини, то пряма їх перетину перпендикулярна до тієї ж пло­щини.

Розв'язання

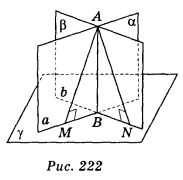
Нехай α γ, β γ, АВ — пряма перетину α і β . Доведемо, що АВ γ (рис. 222). Припустимо, що АВ не перпендикулярна до пло­щини γ. Опустимо з точки А в площинах α і β перпендикуляри до прямих а і b — прямих перетину площин α і β з площиною γ відпо­відно: AMа , ANb. Тоді AMγ , ANγ (із задачі № 58). Отже, з точки А, яка лежить поза площиною γ, проведено дві різні прямі AM і AN, перпендикулярні до площини γ, що неможливо. Таким чи­ном припущення неправильне, отже, АВγ .

3. Задачі № 57, 62 (с. 38—39).

III. Домашнє завдання

§ 3, п. 20; контрольні запитання № 11—12; задача № 56 (с. 38).

IV. Підведення підсумку уроку

Запитання до класу

1. Як розташована пряма, яка лежить в одній із двох перпендикулярних площин і перпендикулярна до лінії перетину цих площин, відносно другої площини?
2. Як розташована лінія перетину двох площин, які перпендикулярні, віднос­но третьої площини, що перетинає їх по перпендикулярних прямих?
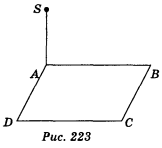
3. ABCD — квадрат, SA (АВС) (рис. 223).

Запишіть площини, які перпендикулярні:

а) до площини SAB;

б) до площини SAD;

в) до площини SBC;

г) до площини АВС;

д) до площин SAB і АВС.

Відповідь, а) (АВС) і (SAD);

б) (SAB) і (АВС);

в) (SAB);

г) (SAB), (SAC), (SAD);

д) (SAD).