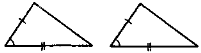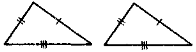Перша ознака рівності трикутників
Тема. Перша ознака рівності трикутників
Мета: домогтися, щоб учні розуміли зміст першої ознаки рівності трикутників та її відмінність від означення рівних трикутників; сформувати в учнів уміння відтворювати зміст теореми, що виражає першу ознаку рівності трикутників, і свідомо доводити теорему, на готовому рисунку знаходити та відбирати рівні елементи трикутників, що відповідають умові першої ознаки рівності трикутників і робити висновок щодо рівності трикутників за знайденими елементами, за текстовим записом виконувати рисунок і, спираючись на отримані раніше знання про властивості відрізків та кутів, робити висновки щодо рівності трикутників на основі першої ознаки трикутників.
Тип уроку: засвоєння знань, вироблення вмінь.
Обладнання: набір креслярського приладдя, таблиця № 13 «Ознаки рівності трикутників».
Хід уроку
І. Організаційний етап
ІІ. Перевірка домашнього завдання
Самостійна робота № 7
Варіант 1
- Трикутник ABC дорівнює трикутнику FED. АВ = 7 см, ВС = 9 см, FD = 6 см. Знайдіть решту сторін кожного трикутника.
-
Трикутник ABC дорівнює трикутнику MNK.
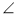 A = 30°,
A = 30°, 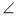 N = 60°,
N = 60°, 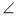 К = = 90°. Знайдіть решту кутів кожного трикутника.
К = = 90°. Знайдіть решту кутів кожного трикутника.
Варіант 2
- Трикутник ABC дорівнює трикутнику KLN. KL = 3 см, LN = 4 см, AC = 5 см. Знайдіть решту сторін трикутників.
-
Трикутник ABC дорівнює трикутнику PQR.
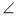 P = 15°,
P = 15°, 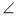 Q = 100°,
Q = 100°, 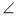 C = = 65°. Знайдіть решту кутів трикутників.
C = = 65°. Знайдіть решту кутів трикутників.
III. Мотивація навчальної діяльності учнів. Формулювання мети і завдань уроку
Необхідність вивчення ознак рівності трикутників стає очевидною для учнів, якщо запропонувати їм для виконання завдання.
-
Про трикутники ABC та МТР відомо, що АВ = МТ, ВС = ТР, АС = МР;
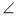 A =
A = 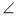 M,
M, 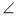 B =
B = 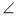 T,
T, 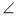 C =
C = 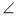 P. Що можна сказати про трикутники ABC та МТР?
P. Що можна сказати про трикутники ABC та МТР?
-
Про трикутники ABC та МТР відомо, що АВ = МТ, АС = МР,
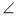 A =
A = 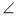 M. Чи будуть рівними трикутники ABC та МТР?
M. Чи будуть рівними трикутники ABC та МТР?
Порівнявши умови завдань, учитель формулює запитання: «Чи можна за рівністю лише деяких (не всіх) елементів трикутника встановити рівність трикутників?». Пошук відповіді на це запитання, а точніше пошук того найменшого набору відповідно рівних елементів трикутників, за якими можна встановити рівність трикутників, і є основною метою вивчення питання про ознаки рівності трикутників.
IV. Актуалізація опорних знань і вмінь учнів
Усні вправи
- Відомо, що трикутники у кожному з випадків на рис. 66 (а—г) попарно рівні. Виділіть рівні елементи й виконайте відповідні записи.
Які елементи названих трикутників є спільними?
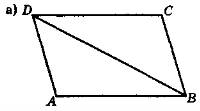

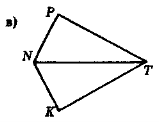
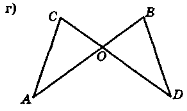
Рис. 66
- На сторонах рівних кутів В і В1 відкладено рівні відрізки ВА = В1А1 і ВС = В1С1. У результаті накладення кути В і В1 та відрізки ВА і В1А1 сумістяться. Чи сумістяться в результаті такого накладання відрізки ВС і В1С1?
- Чи є рівними кути на рис. 67? Відповідь обґрунтуйте.
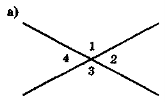
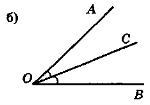
Рис. 67
V. Засвоєння нових знань
План вивчення нового матеріалу
- Відмінність між ознакою та означенням рівності трикутників.
- Перша ознака рівності трикутників та її доведення.
- Приклад застосування першої ознаки рівності трикутників.
Методичний коментар
Формулювання теореми, що виражає першу ознаку рівності трикутників в даному навчальному посібнику не відрізняється від традиційного (підручник О.В.Погорєлова тощо), але доведення на відміну від традиційного здійснюється із посиланням не на аксіоми про відкладання відрізків та кутів, які вивчались раніше, а на означення рівних фігур як таких, що пристають при переміщенні.
Слід зазначити, що як під час доведення теореми, так і під час її використання для доведення рівності трикутників (особливо на початковому етапі), значну роль відіграє наочність. Тому ефективним є прийом позначення однаковим кольором (або лініями однакової ширини, або однаковими позначками) рівних за умовою (а потім за доведенням) елементів. Цей прийом допомагає також учням «побачити» план розв'язування задачі, тому вже на перших уроках слід привчати учнів розпочинати розв'язування задач на доведення рівності трикутників саме з позначення їх рівних елементів. На початковому етапі вивчення теми доречним є використання таблиці № 13 «Ознаки рівності трикутників».
Таблиця № 13
Ознаки рівності трикутників
|
|
За двома сторонами і кутом між ними |
|
|
За стороною і двома прилеглими кутами |
|
|
За трьома сторонами |
VI. Первинне усвідомлення матеріалу
Усні вправи
- Між якими сторонами трикутника MNK лежать кути М, N, K?
- Які ще, крім позначених, елементи трикутників мають бути рівними, щоб можна було встановити рівність трикутників за першою ознакою рівності трикутників (рис. 68)?
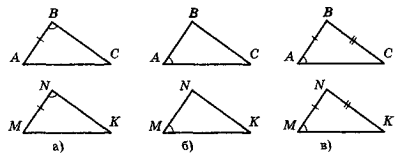
Рис. 68
VІІ. Вироблення вмінь учнів
Письмові вправи
- На рис. 69 зображені пари рівних трикутників. Дайте обґрунтування рівності трикутників ABC і A1В1С1 у кожному з випадків а – в.
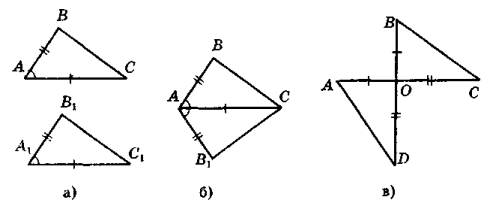
Рис. 69
- За даними доведіть рівність трикутників (рис. 70).
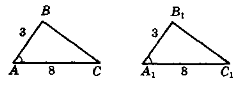
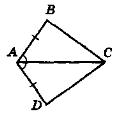
Рис. 70
- № 351 (а), 354, 356, 357, 358 (підручник).
Методичний коментар
Як уже було сказано вище, розв'язання задач на доведення рівності трикутників слід починати з виокремлення рівних елементів трикутників, даних в умові задачі, а потім уже визначати, рівність яких елементів слід довести, щоб можна було зробити висновок про рівність трикутників за ознакою. Бажано привчати учнів одразу до стандартної форми міркувань:
Розглянемо трикутники...
У них:
A) ... = ... (обґрунтування рівності першої пари рівних елементів);
Б) ... = ... (обґрунтування рівності другої пари відповідних елементів);
B) ... = ... (обґрунтування рівності третьої пари рівних елементів).
Тому трикутник ... дорівнює трикутнику ... за ... (коротке формулювання ознаки).
VIII. Підсумки уроку
Чи можна твердити, що трикутник ABC дорівнює трикутнику DEF, якщо AB = DE , AC = DF, ![]() A =
A = ![]() E? чому?
E? чому?
IX. Домашнє завдання
- § 12, с. 93 (теорема 10 з доведенням).
- Письмово: № 355, 364.
- На повторення: задача, подібна до задач № 1, 2 (див. самостійну роботу № 2, с. 71).


про публікацію авторської розробки
Додати розробку