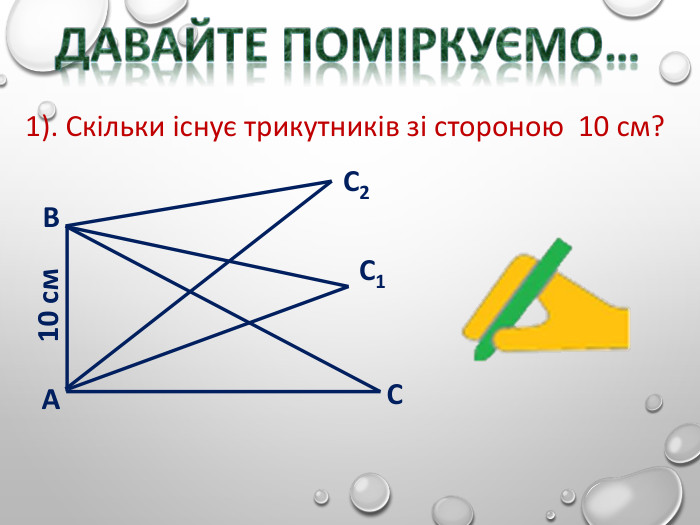
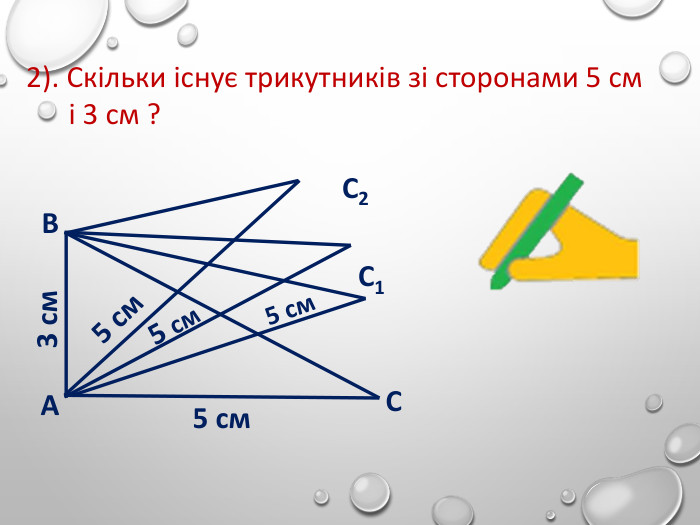
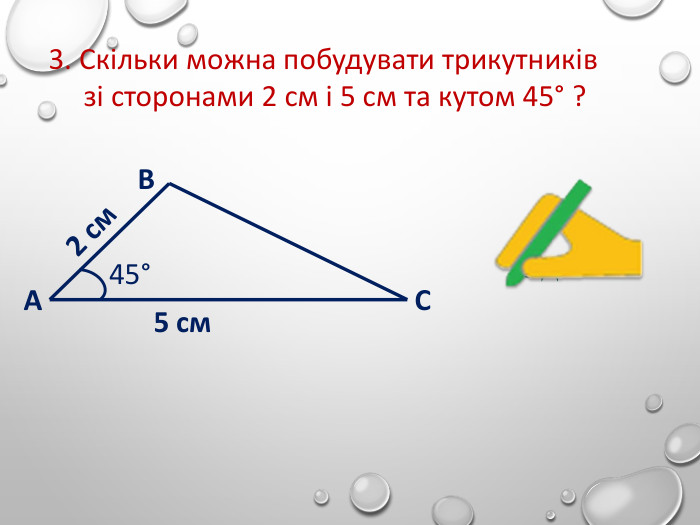
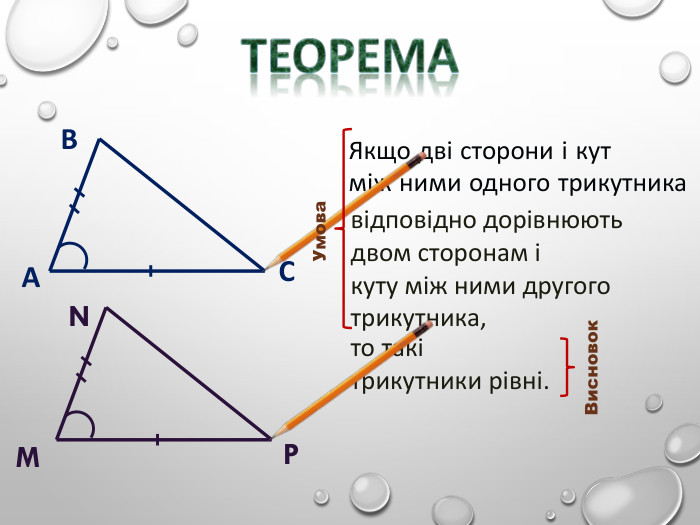
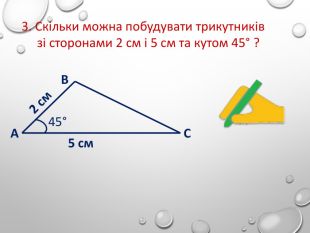
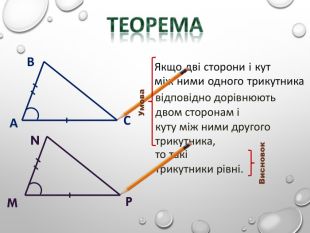
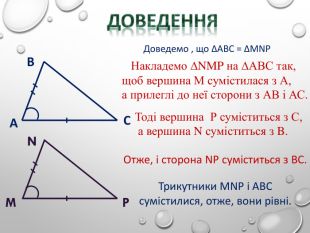
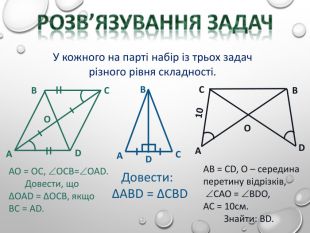
Перша ознака рівностітрикутників
Про матеріал
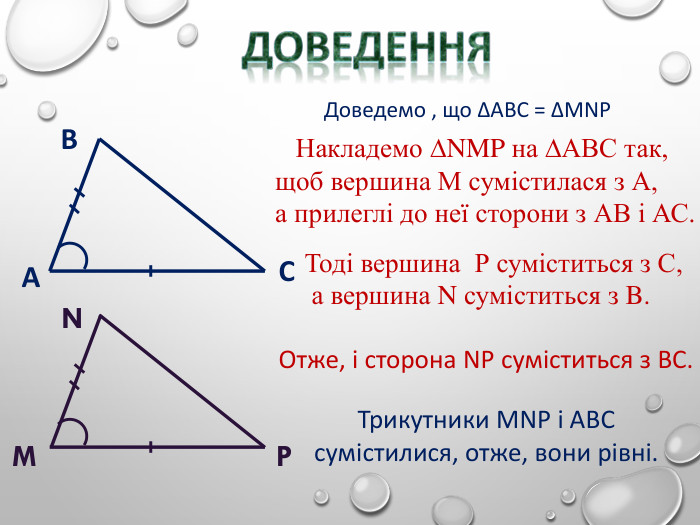
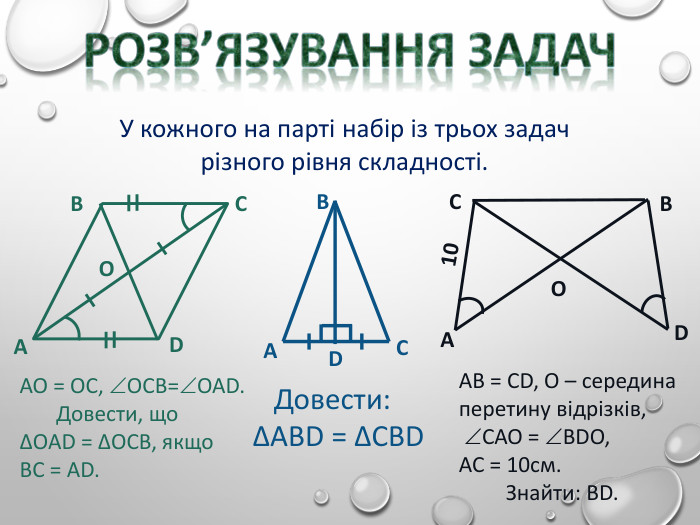
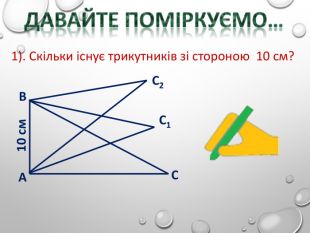
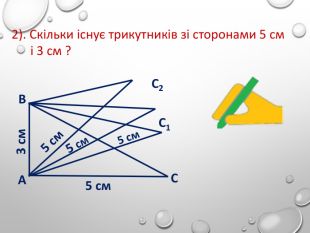
Презентація до уроку з 1 ознаки рівності трикутників. Для учнів 7-го класу. З малюнками та поясненнями Перегляд файлу
Зміст слайдів
ppt
До підручника
Геометрія.(підручник) 7 клас (Тадеєв В.О.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку