Підсумкова контрольна робота з алгебри, 10 клас                    Варіант – 1

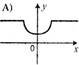
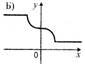
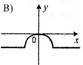
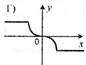
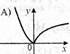
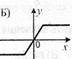
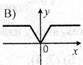
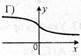
1.  На якому з рисунків зображено графік непарної функції?                                         (0,5)

2.Як треба перенести паралельно графік функції y sin x , щоб отримати графік

функції y  ^sinx^?                                                                                                                  (0,5)

                                           4 

3.Чому дорівнює значення виразу: ⁵ 7  17 ⁵ 7  17                                                     (0,5)

4.Обчислити значення виразу: 2^0,7 ³ 2^0,9 .                                                                            (0,5)

5.Яке число є періодом функції у = sin(2x –5)?                                                                      (0,5)

6.Обчислити значення виразу: cos75°·cos15°  –  sin75°· sin15°.                                     (0,5)

7.Знайти множину значень функції у = sinx – 2 .                                                                  (0,5)

6-x

8.Вказати область визначення функції  f(x)  ₆ 3x-9 .                                                    (0,5)

9.Чому дорівнює кутовий коефіцієнт дотичної до графіка функції у = х² – 3х у точці     з абсцисою х₀=-1?                                                                                                                           (0,5)

10.Спростити вираз: ^cos^^sin.                                                                          (0,5)   

                                                                2       

11.Скласти рівняння дотичної до графіка функції  f(x)=x³−5x  у точці 

     з абсцисою х₀=2.                                                                                                                             (1б) 12. Розв´язати рівняння: 23x x3 .                                                                                 (2б)

13.  Знайти корені рівняння cos(3x ^) 1 на проміжку [-π;2π].                                (2б) 4

14.  Знайти проміжки зростання, спадання, точки екстремуму та екстремум  x² 5x

       функції f (x)     .                                                                                                               (2б) 

x   4

Підсумкова контрольна робота з алгебри, 10 клас                    Варіант – 2

1.  На якому з рисунків зображено графік парної функції?                                              (0,5)                

2.  Як треба перенести паралельно графік функції ycosx , щоб отримати графік

функції y cosx -^?                                                                                                                  (0,5)                     

6

3.Чому дорівнює значення виразу: ⁷ 3 2 2 ⁷ 32 2                                                     (0,5)

4.Обчислити значення виразу: 16^0,75 25^0,5 .                                                                       (0,5)

5.Яке число є періодом функції у = tg(2x +2)?                                                                        (0,5)

7.Знайти множину значень функції у = cosx – 5 .                                                                 (0,5)

5-x

 8.Вказати область визначення функції  f(x)  ₄ 2x_8 .                                                   (0,5)

9. Матеріальна точка рухається за законом S(t)=3t²  – 3 . Знайти швидкість  тіла в

момент часу t=3                                                                                                                                  (0,5)

10.Спростити вираз: ^ctg^^tg.                                                                          (0,5)   

                                                               2     

1 ³

11.Скласти рівняння дотичної до графіка функції  f(x)  4x - x в точці  3

     з абсцисою  х₀=3.                                                                                                                            (1б)

12.Розв´язати рівняння:    78xx6 .                                                                           (2б)

13.Знайти корені рівняння sin(4x ^) 1 на проміжку [-2π;π].                                  (2б) 6

14.Знайти проміжки зростання, спадання, точки екстремуму та екстремум функції  x² 6x

    f (x)     .                                                                                                                                    (2б) 

x2