Презентація до уроку-узагальнення з теми "Тригонометричні функції" для учнів 10 класу
Про матеріал
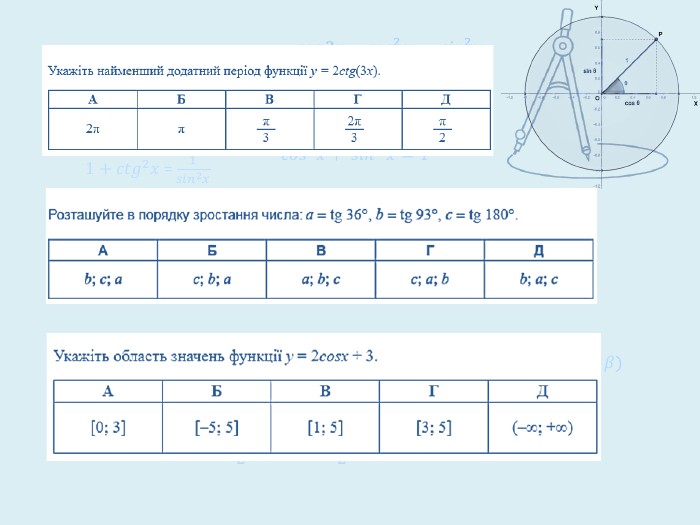
Презентація для проведення узагальнюючого уроку з теми "Тригонометричні функції". Дана розробка містить посилання на динамічне геометричне середовище для побудови графіків GeoGebra та посилання на інтерактивні вправи, створені в сервісі LearningApps. Крім того, в презентації є завдання із ЗНО минулих років з даної теми. Слайди презентації логічно зв'язані і проведений за допомогою неї урок буде захоплюючим та результативним. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра і початки аналізу (академічний рівень) 10 клас (Нелін Є.П.)
До уроку
РОЗДІЛ 3. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку