Підсумкова контрольна робота з вищої математики
Варіант 1
Завдання 1
1. Нехай φ – кут нахилу прямої y kx b до додатного напрямку вісі ОХ, оберіть вірне твердження:
А) k tg Б) k ctg В) k sin Г) k cos
![]()
![]() 1 0 0
1 0 0
2. Обчислити визначник: 2 3 4
1 1 2
А) -2 Б) 2 в) 1 Г) 0
3. Функція виду ![]() є:
є:
А) степенево-показниковою функцією
Б) складеною функцією
В) функцією , заданою параметрично
Г) неявною функцією
Д) дробово-раціональною функцією
cosx
4. Знайти значення похідної функції f (x) ![]() в точці x0
в точці x0 ![]()
1 sinx 2
|
А) 0 Б) 0,5 В) 2 1 x2dx 5. Обчислити інтеграл 0 |
|
Г) -0,5 |
![]()
![]()
![]()
![]() А) Б) В) Г)
А) Б) В) Г)
|
6. Розв’язками рівняння y y 0 є функції: |
|
|
А) y1 ex, y2 ex Б) y1 x, y2 x2 |
В) y1 x ex, y2 ex |
Завдання 2
x3
1. Обчислити інтеграл ![]() (6x4 5)5 dx
(6x4 5)5 dx
r r
2. Дано вектори а(4;6;7) і b(5;8;10). Знайти абсолютну величину вектора
r r
3a+2b;
Підсумкова контрольна робота з предмету «Вища математика»
Варіант 2
Завдання 1
1. Із всіх прямих вибрати пряму перпендикулярну даній: 2x 3y 7 0
А) 2x 3y 7 0 Б) 6x 4y 7 0 В) 3x 2y 1 0 Г) 2x 3y 7 0
2 1 3 5 1
2. Знайти добуток матриць A0 1;B1 0 1
5 5 1 5 0 1 5 10 1 0 5 1
А) 1 1 1 Б) 1 1 1 В) 1 0 1 Г) 1 1 1
3. Невизначеним інтегралом функції y = f (x) називається
А) первісна функції y=f(x)
Б) сума всіх первісних функції y=f(x)
В) добуток всіх первісних функції y=f(x)
Г) сукупність всіх первісних функції y=f(x)
4 . Знайти похідну функції y 2х4 cosx 3
А) y sinx 8x3 3 Б) y 8x3 sin x В) y 8x3 sinx 3
Г) y sinx 8x3
![]()
2
5. Обчислити інтеграл sinxdx
![]()
3
А)1,5 Б) 0,5 в) -1,5 Г) -0,5
6. Розв’язки характеристичного рівняння дорівнюють 1 і 2. Тоді відповідне лінійне однорідне рівняння має вид:
А) y y 2y 0 Б) y 3y 2y 0 В) y 3y 2y 0
Завдання 2
1. Обчислити інтеграл tg(x)dx
2. Розв’язати задачу Коши y 6y5y 0, y01, y0 1
Варіант 3
Завдання 1
1. Є рівняння прямої 2x 3y 4 0 . Знайти кутовий коефіцієнт даної прямої.
А) k ![]() Б) k
Б) k ![]() В) k
В) k ![]() Г) k
Г) k ![]()
0 ![]()
![]() 1 1
1 1
2. Обчислити визначник: 1 0 1
1 1 0
А) 0 Б) 2 В) -2 Г) 1
3. Функція називається складеною, якщо
А) функція є сумою або різницею кількох функцій
Б) функція є добутком декількох функцій
В) аргументом цієї функції є інша функція
Г) вірної відповіді нема
1 ![]()
4. Знайти значення похідної функції y5 x в точці x0 1
А) -5ln5 Б) ![]() В) 5ln5 Г)
В) 5ln5 Г) ![]()
0
5. Обчислити інтеграл x2 6xdx
2
А) ![]() Б)
Б) ![]() В) 8 Г) -8
В) 8 Г) -8
6. Кількість довільних сталих в загальному розв’язку звичайного диференційного рівняння третього порядку дорівнює:
А) 2 Б) 4 В) 3 Г) 1
Завдання 2
sinx
1. ![]() Обчислити інтеграл 3 cos2 x dx
Обчислити інтеграл 3 cos2 x dx
r r
2. При яких значеннях n вектори a(1;2;6) і b(2;5;n) перпендикулярні?
Підсумкова контрольна робота з предмету «Вища математика»
Варіант 4
Завдання 1
1. Дано пряму 5x+3 y-3=0. Визначити кутовий коефіцієнт прямої паралельної даній:
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
4 3
2. Знайти f (x) 5x, де x22 1
20 15 20 15 5 15 20 110
А) 110 5 Б) 110 5 В) 110 20 Г) 15 5
3. Розв’язати диференціальне рівняння – це
А) знайти значення функції, яке перетворює рівняння в тотожність
Б) знайти функцію, яка перетворює рівняння в тотожність
В) знайти значення аргументу, яке перетворює рівняння в тотожність Г) вірної відповіді нема
4. Знайти похідну функції z ln(x2 4x) в точці -1 А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
2 1
5. Вкажіть первісну функції f (x)3x ![]() на проміжку (0; + ∞)
на проміжку (0; + ∞)
x
![]()
![]()
![]() А) F(x)3 x12 Б) 3 x1 3 ln x Г) F(x) x3 ln x F(x) x 2 В) F(x) x 3
А) F(x)3 x12 Б) 3 x1 3 ln x Г) F(x) x3 ln x F(x) x 2 В) F(x) x 3
6. Нехай число 1 є кратний корінь характеристичного рівняння. Тоді відповідне лінійне диференційне рівняння зі сталими коефіцієнтами має вид:
А) y y 0 Б) y 2y y 0 В) y 2y y 0
Завдання 2
x4 8x2
1. Обчислити похідну функції y ![]() x2 1 в точці х=1
x2 1 в точці х=1
2. При яких значеннях y і z вектори ar(15;y;1) і вr(18;12;z) колінеарні?
Варіант 5
Завдання 1
1. Якщо дві прямі перпендикулярні, то їх коефіцієнти задовольняють формулі:
А) k1 k2 Б) k1 k2 1 В) k1 k2 1 Г) k1 k2 1
![]()
![]() 4 0 5
4 0 5
2. Обчислити визначник: 2 1 2
5 0 7
А) 3 Б) -3 В) 0 Г) 9
3. Похідною функції y=f(x) називається: А) границя відношення значення функції до значення аргументу, за умови, що аргумент прямує до нуля
Б) відношення значення функції до значення аргументу
В) відношення приросту функції до приросту аргументу
Г) границя відношення приросту функції до приросту аргументу, за умови, що приріст аргументу прямує до нуля
4. Знайти похідну функції y 2x4 x 5 в точці х=-1
1) -9 2) 7 3) -1 4) -7
1
5. Вкажіть первісну функції f (x) 2x ![]() на проміжку (0; + ∞) x
на проміжку (0; + ∞) x
![]()
![]() 1 2 1 В) F(x) x2 lnx Г) F(x) 2x ln x
1 2 1 В) F(x) x2 lnx Г) F(x) 2x ln x
А) F(x) 2 x2 Б) F(x) x x2
6. Знайдіть корені характеристичного рівняння диференційного рівняння y 9y 0 А) k1 3,k2 3 Б) k1 0,k2 3 В) k1 1,k2 9
Завдання 2
2ln2 x 3
1. Обчислити інтеграл ![]() x dx
x dx
2. Дано вектори аr(1;0;2) і вr(3;1;1). Знайти абсолютну величину вектора 3аr+2вr.
Варіант 6
Завдання 1
1. Визначити точки, що належать даній прямій 2x-3y-3=0
М1(3;1); М2(2;3); М3(6;3); М4(-3;-3); М5(3;-1); М6(-2;1)
2. Визначити півосі гіперболи 9x2 64y2 1
А) a ![]() ;b
;b ![]() Б)a 3;b 8 В) a 9;b 64 Г) a
Б)a 3;b 8 В) a 9;b 64 Г) a ![]() ;b
;b ![]()
3. Похідною другого порядку називається
А) квадрат похідної першого порядку
Б) квадратний корінь від похідної першого порядку
В) похідна від похідної першого порядку
Г) вірної відповіді немає
4.Знайти похідну функції y 4x3 xex в точці х=0 А) 1 Б) е В) –е Г) -1
5. Вкажіть первісну функції f (x) 3x2 sinx
А) F(x) x3 cosx Б) F(x) sinx 2x В) F(x) x3 cosx x3
Г) F(x) ![]() cosx
cosx
3
6. Знайдіть розв’язок рівняння y 2y 5y 0.
А) y C1ex C2ex Б) y (C1ex C2ex)cos2x В) y ex(C1 cos2x C2 sin2x) Г) y C1e5x C2e2x
Завдання 2
2
1. ![]() Обчислити інтеграл 3 43x dx
Обчислити інтеграл 3 43x dx
r r
2. При яких значеннях n скалярний добуток векторів a(1;2;6) і b(2;5;n) дорівнює 6?
Варіант 7
1. Якщо дві прямі паралельні, то їх коефіцієнти задовольняють формулі:
А) k1 k2 Б) k1 k2 1 В) k1 k2 1 Г) k1 k2 1
![]()
![]() 6 0 0
6 0 0
2. Обчислити визначник: 2 1 0
3 2 1
А) 7 Б) -7 В) 6 Г) -6
3. Задачею Коші називається задача знаходження розв’язку диференціального
рівняння ![]() , який
, який
А) задовольняє дане рівняння
Б) задовольняє дане рівняння при C = 0
В) задовольняє дане рівняння при будь-якому значенні C
Г) задовольняє умову y(x0) = y0
|
4. Знайти похідну функції f (x) 2x14 |
|
|
А) 42x13 Б) 82x 1 В) 8x2x13
|
Г) 82x13 |
5. Знайти невизначений інтеграл:![]()
![]() A)
A) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
6. Знайдіть розв’язок рівняння y 6y 9y 0.
А) y C1e3x C2e3x Б) y C1 cos3x C2 sin3x В) y C1 C2e3x Г) y C1e3x C2xe3x
Завдання 2
1. ![]() Обчислити похідну функції y 5x2 1 3 x в точці х=1 x
Обчислити похідну функції y 5x2 1 3 x в точці х=1 x
2 ![]()
![]() 2 2 2
2 2 2
2 4 2 4
2. Обчислити визначник:
2 2 6 2
2 4 2 8
Варіант 8
Завдання 1
1. Установити, які з наступних прямих перпендикулярні:
3x4y10 6x15y70 7x2y10 5x7y30
А) Б) В) Г)
4x3y70 10x4y30 4x6y170 3x2y50
2. Знайти f (x) x2 4x , де x 21 10
7 5 12 0 12 0 7 5
А) 0 10 Б) 7 5 В) 7 5 Г) 0 10
3. Сукупність n розв’язків лінійного однорідного диференціального рівняння n-го порядку, які визначені і лінійно незалежні на проміжку (a; b) називається
А) частинною системою розв’язків
Б) незалежною системою розв’язків
В) фундаментальною системою розв’язків
Г) загальним розв’язком
4. Знайти похідну функції y 4x2 2x 7
А) 8x+9 Б) 4x+2 В) 8x+2 Г) 8x
5. Визначити півосі еліпса 16x2 y2 16
А) a 4;b 1 Б)a ![]() ;b 1 В) a 16;b 1 Г) a 1;b 4
;b 1 В) a 16;b 1 Г) a 1;b 4
6. Порядок диференційного рівняння – це:
А) максимальний порядок похідної шуканої функції
Б) максимальний степінь шуканої функції
В) максимальний степінь аргументу шуканої функції
Г) кількість операцій при його рішенні
Завдання 2
x4 8x2
1. Обчислити похідну функції y ![]() x2 1 в точці х=1
x2 1 в точці х=1
![]()
![]() 3 1 1 1
3 1 1 1
2. Обчислити визначник: 2 1 1 1
8 5 9 5 7 7 7 4
Варіант 9
|
x2 x1 y2 y1 |
|
Б) Ax By Cz D 0 |
|
x y
|
|
Г) y y0 kx x0 |
|
3. Обчислити визначник: 4 2 2 3 |
1 0 |
|
|
А) -1 Б) 1 В) 2
3. Функція виду ycosxctg2x є: |
|
Г) -2 |
1. Вкажіть формулу, яку треба використовувати для того, щоб написати рівняння прямої, яка проходить через дві точки. x x y y
А) степенево-показниковою функцією
Б) складеною функцією
В) функцією , заданою параметрично
Г) неявною функцією
Д) дробово-раціональною функцією
cosx
4. Знайти значення похідної функції f (x) ![]() в точці x0
в точці x0 ![]()
1 sinx 2
А) 0 Б) 0,5 В) 2 Г) -0,5
5. Обчислити інтеграл ![]()
А) -9 Б) 9 В) 12 Г) 3
6. Диференційному рівнянню y 4y 0 відповідає характеристичне рівняння:
А) k2 4k 0 Б) 2k40 В) k2 4 0 Г) k2 4 0
Завдання 2
3x2dx
1. Обчислити інтеграл ![]() (15x3)3
(15x3)3
2. Розв’язати диференціальне рівняння y''-7y'+6y=0, y(0)=5, y'(0)=3
Завдання 1
1.Дано пряму 2x+3y+4=0. Скласти рівняння прямої, що проходить через точку М(2;1) паралельно даній прямій:
А) -2x+3 y-2=0 Б)2x+3y+10=0 В)2 x-3y-3=0 Г) -2 x-3y+7=0
2. Знайти f (x) 2x2 2x , де x02 14
16 0 16 0 0 16 0 16
А) 0 16 Б) 0 16 В) 16 0 Г) 16 0
3. Який метод треба застосувати для знаходження інтегралу ![]()
А) за таблицею Б) по частинам
В) піднесення під диференціал Г) заміни
4. Знайти похідну функції f (x) x2 xcosx в точке x0 0
А) -1 Б) 0 В) 1 Г) 2
5. Дано точки А(2;3;1), В(3;4;2), координати вектора АВ дорівнюють:
А) (5;7;3); Б) (-1;-1;-1); В) (-5;-7;-3) Г) (1;1;1)
4. Диференційному рівнянню y 3y 0 відповідає характеристичне рівняння:
А) k2 3k 0 Б) k2 3k 0 В) k2 3 0 Г) k2 3 0
Завдання 2
1. Розв’язати диференціальне рівняння y''-9y'+14y=0, y(0)=2, y'(0)=-1
![]() 1 2 1 4
1 2 1 4
1 3 0 6
2. ![]() Обчислити визначник:
Обчислити визначник:
2 2 1 4
3 1 2 1
Варіант 11
1. Вкажіть рівняння прямої, яка має даний кутовий коефіцієнт k ![]()
А) 7x 8y 12 0 Б) x 8y 4 0 В) 7x y 2 0 Г) 7x 8y 12 0
![]()
![]() 0 1 0
0 1 0
1 3
2. Обчислити значення виразу detA X , де А= 01 11 11, X 2 0
2 6 1 3 1 3 2 6
А) 4 0 Б) 2 0 в) 2 0 Г) 4 0
3. Функція виду x cos33tt є:
y sin
А) степенево-показниковою функцією
Б) складеною функцією
В) функцією , заданою параметрично
Г) неявною функцією
Д) дробово-раціональною функцією
4. Вкажіть первісну функції f (x) 3x2 cosx
А) F(x) x3 cosx Б) F(x) sinx 2x
F(x) x3 sinx Г) F(x) x3 cosx
В)
5. 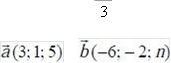 При якому значенні n вектори і колінеарні?
При якому значенні n вектори і колінеарні?
А) -5 Б) 10 В) -10 Г) 0
6. Характеристичному рівнянню k2 3k 4 0відповідає диференційне рівняння:
А) y 3y 4y 0 Б) y 3y 4y 0 В) y 3y 4 0 Г) y 3y 4 0
Завдання 2
1. Задано трикутник ABC : A(−2, 3), B(4, 1), C(6, −5). Написати рівняння медіани, яка проведена з вершини A.
|
11 12 2.Обчислити визначник: 13 3. |
11 10 11 12 |
12 11 10 11 |
13 12
10
|
Завдання 1
1. Знайти кутовий коефіцієнт прямої, що проходить через точки А(3;2) і В(5;-2)
А) -2 Б) ![]() В) 2 Г)
В) 2 Г) ![]()
2 , де X 12 10 2. Знайти значення f (x) det(X ) X
0 1 1 0 0 1 1 0
А) 1 4 Б) 4 1 В) 1 4 Г) 4 1
А) 15 Б) Г)13
4. Загальне рішення однорідного диференціального рівняння 2-го порядку має вигляд y C1x C2e3x . Визначити корінь характеристичного рівняння А) 1; -3 Б) -3; 0 В) -3; -3 Г) 3; 3
1
5. ![]() Обчислити інтеграл x3 x2dx
Обчислити інтеграл x3 x2dx
0
![]()
![]()
![]() А) Б) В) 1 Г)
А) Б) В) 1 Г)
6. Знайдіть похідну функції f (x) (2x 3)8
А) f (x) 16(2x 3)7 Б) f (x) 24(2x 3)7 В) f (x) 8(2x 3)7 Г) f (x) 8(2x 3)7
Завдання 2
x3dx
1. ![]() Обчислити інтеграл x8 5
Обчислити інтеграл x8 5
2. Дано еліпс 9x2+5y2=45. Знайти його ексцентриситет
Варіант 13
Завдання 1
1. З всіх прямих вибрати пряму перпендикулярну даній: 2x 3y 7 0
А) 2x 3y 7 0 Б) 6x 4y 7 0 В) 3x 2y 1 0 Г) 2x 3y 7 0
3 4
2. Знайти f (x) 3x det(x) I , де X 2 1, а І - одинична
9 12 2 12 2 12 8 11
А) 6 3 Б) 6 8 В) 6 8 Г) 5 2
3. Рівняння виду ![]()
А) канонічним рівнянням кола Б) канонічним рівнянням еліпса
В) канонічним рівнянням гіперболи Г) канонічним рівнянням параболи
4. Знайти значення похідної функції f (x) e4x e2x2 в точці x0 0
А) 4 Б) 2 В) 3 Г) 5
1
5. Обчислити інтеграл x2dx
0
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
6. Є диференційне рівняння y 2y y 0 . Коренями відповідного характеристичного рівняння є:
А) k1 Б) k1 В) k1 k2 1 Г) k1 k2 1
Завдання 2
1. Задані вершини M1(2, 3), M2(−1, 2) i M3(4, 5) трикутника. Скласти рівняння сторони М1М2.
2. Обчислити ексцентриситет еліпсу 25x2+9y2=1
Завдання 1
1. Знайти кут ( у градусах) нахилу прямій -4x-4y+9=0
А) 45º Б)135º В) 60º Г) 90?
2. Визначити координати центра окружності x12 y32 16 А) C(-1;3) Б) C(0;0) В) C(1; -3) Г) C(1; 1)
![]()
![]() 3 2 5
3 2 5
3. Обчислити визначник 3 2 4
0 2 0
А) -5 Б) 5 В) -6 Г) 6
4. Рівняння кола радіуса r з центром у початку координат має наступний вигляд…
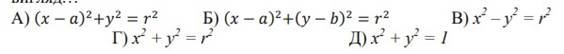
5. Загальне рішення однорідного диференціального рівняння 2-го порядку має вигляд y C1e5x C2e7x . Визначити добуток коренів характеристичного рівняння
А)-35 Б) 35 В) 5 Г) -7
1
6. ![]() Обчислити інтеграл x3 4 xdx
Обчислити інтеграл x3 4 xdx
0
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
Завдання 2
1. ![]() Обчислити інтеграл sinx cosxdx
Обчислити інтеграл sinx cosxdx
![]()
![]() 3 9 3 6
3 9 3 6
2. Обчислити визначник: 5 8 2 7
4 5 3 2 7 8 4 5
Завдання 1
1. Знайти рівняння прямої, яка має кутовий коефіцієнт k ![]()
А) 7x 8y 12 0 Б) x 8y 4 0 В) 7x y 2 0 Г) 7x 8y 12 0
1 2
2. Знайти f (x) det(3x 2I) , де X 2 0, а І - одинична
А) -31 Б) 20 В) 34 Г) 31
3. 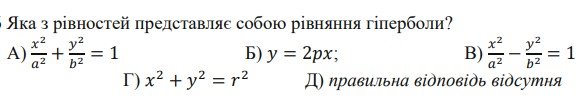
4. Знайти похідну функції в точці y ![]() x3 x2 в точці x0 1
x3 x2 в точці x0 1
3
А) -3 Б) 3 В) 2 Г) -2
5. Вкажіть первісну функції f (x) 4х3 х2
4 3
![]() А) F(x) 12х2 2х Б) F(x) 4х2 х3 В) F(x) х х
А) F(x) 12х2 2х Б) F(x) 4х2 х3 В) F(x) х х
4 3
3
Г) F(x) х4 ![]() х
х
3
6. Диференційне рівняння y 4y 4y 0 має загальний розв’язок:
А) y e2xC1 C2x Б) y C1e2x C2e2x В) y e2x(1 x) Г) y e2x xe2x C
Завдання 2
1. Знайти точку перетину прямих 2x y 3 0 та 4x 3y 11 0. У відповідь записати суму координат.
2. ![]() Знайти похідну функції y 13x2x2
Знайти похідну функції y 13x2x2
Підсумкова контрольна робота з предмету «Вища математика»
Варіант 16
Завдання 1
1. Дано пряму 5x+3 y-3=0. Визначити кутовий коефіцієнт k прямої паралельної даній
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
![]()
![]() 4 3 2
4 3 2
2. Обчислити визначник 3 0 4
2 1 3
А) 12 Б) 15 В) -13 Г) -10
3. ![]() Дани вектори
Дани вектори a 1;2;10, b 4;2;0. Знайти кут між векторами
А) 90º Б) 45° В) 180° Г) 0°
4. Який метод треба застосувати для знаходження інтегралу ![]()
А) за таблицею Б) по частинам
В) піднесення під диференціал Г) заміни
![]()
2
5. Обчислити інтеграл sin2xdx
![]()
3
1)1,5 2) 0,25 3) -1,5 4) -0,25
6. Розв’язками рівняння y y 0 є функції:
А) y1 ex, y2 ex Б) y1 x, y2 x2 В) y1 xex, y2 ex
Завдання 2
![]()
![]() 3 2 2 2
3 2 2 2
1. Обчислити визначник: 2 3 2 2
2 2 3 2
2 2 2 3
2. Задані вершини M1(2, 3), M2(−1, 2) i M3(4, 5) трикутника. Скласти рівняння сторони М1М3.
1. З даних рівнянь вибрати рівняння еліпса із центром на початку координат і півосями а=4 і b=5
![]()
![]() А) x2 y2 1 Б) x2 y2 1 В) 16x2 25y2 400 Г) 25x2 16y2 400
А) x2 y2 1 Б) x2 y2 1 В) 16x2 25y2 400 Г) 25x2 16y2 400
25 16 25 16
![]()
![]() 4 0 5
4 0 5
2. Обчислити визначник: 2 1 2
5 0 7
А) 3 Б) -3 В) 0 Г) 9
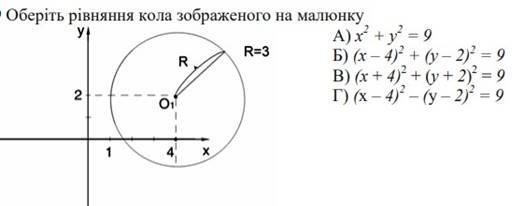
3. 
cosx
4. Знайти значення похідної функції f (x) ![]() в точці x0
в точці x0 ![]()
1 sinx 2
А) 0 Б) 0,5 В) 2 Г) -0,5
1
5. ![]() Обчислити інтеграл 8 x5dx
Обчислити інтеграл 8 x5dx
0
А) ![]() Б)
Б) ![]() В)
В) ![]() Г) 1
Г) 1
6. Розв’язки характеристичного рівняння дорівнюють 1 і 2. Тоді відповідне лінійне однорідне рівняння має вид:
А) y y 2y 0 Б) y 3y 2y 0 В) y 3y 2y 0
Завдання 2
1. Обчислити інтеграл xcos(x2 1)dx
2. Розв’язати задачу Коші y''-6y'+8y=0, y(0)=3, y'(0)=1
1. Із всіх прямих вибрати пряму перпендикулярну даній: 2x 3y 7 0
А) 2x 3y 7 0 Б) 6x 4y 7 0 В) 3x 2y 1 0 Г) 2x 3y 7 0
2. Знайти f (x) x2 3x, де x12 14
4 20 4 20 4 20 4 20
А) 10 4 Б) 10 4 В) 10 4 Г) 10 4
3. 
4. Знайти похідну функції y x3x
А) y 3 x3x1 x3x ln x Б) y x3x1 3x3x ln x
В) y 3x x3x1 3x3x ln x Г) y 3x 3x3x ln x
5. Обчислити інтеграл cosxdx
![]()
2
1) -1 2) 1 3) 0 4) 2
3.
6. Кількість довільних сталих в загальному розв’язку звичайного диференційного рівняння четвертого порядку дорівнює:
А) 2 Б) 4 В) 3 Г) 1
Завдання 2
1. Обчислити інтеграл 2x2 xdx
2. Знайдіть значення довільних сталих при розв’язуванні задачі Коші для лінійного диференціального рівняння зі сталими коефіцієнтами:
y7y10y 0, y01, y01
1. ![]() Установити, яку лінію визначає рівняння y 25 x2
Установити, яку лінію визначає рівняння y 25 x2
А) гіпербола Б) еліпс В) верхня половина окружності Г) нижня половина окружності
![]()
![]() 0 1 0
0 1 0
2. Обчислити визначник: 4 2 1
2 3 0
А) -1 Б) 1 В) 2 Г) -2
3. 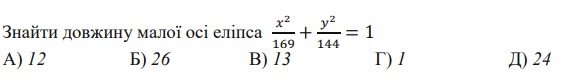
4. Знайти похідну функції f (x) 2x14
А) 42x13 Б) 82x 1 В) 8x2x13 Г) 82x13
0
5. Обчислити інтеграл x2 6xdx
2
А) ![]() Б)
Б) ![]() В) 8 Г) -8
В) 8 Г) -8
6. Нехай число -1 є кратний корінь характеристичного рівняння. Тоді відповідне лінійне диференційне рівняння зі сталими коефіцієнтами має вид:
А) y y 0 Б) y 2y y 0 В) y 2y y 0
Завдання 2
3e2x
1. ![]() Обчислити інтеграл e4x 4dx
Обчислити інтеграл e4x 4dx
2. Обчислити найкоротшу відстань від точки А(6,-8) до окружності, x2+y2=9
1. Знайти кут ( у градусах) нахилу прямій -4x-4y+9=0
А) 45º Б)135º В) 60º Г) 90?
![]()
![]() 6 0 0
6 0 0
2. Обчислити визначник: 2 1 0
3 2 1
А) 7 Б) -7 В) 6 Г) -6
3. При якому значенні p вектори ![]() і взаємно перпендикулярні? А) -10 Б) 5 В) 10 Г) -5
і взаємно перпендикулярні? А) -10 Б) 5 В) 10 Г) -5
4. Знайти значення похідної функції y x2 sin x в точці x0 А) 2 1 Б) 21 В) 21 Г) 2
5. Знайти півосі гіперболи 21x2 43y2 903
![]()
![]() А) a=43, b=21 Б) a=21, b=43 В) a 43;b 21 Г) a 21;b 43
А) a=43, b=21 Б) a=21, b=43 В) a 43;b 21 Г) a 21;b 43
6. Знайдіть корені характеристичного рівняння диференційного рівняння y 9y 0
А) k1 3,k2 3 Б) k1 0,k2 3 В) k1 3i, k2 3i
Завдання 2
1. ![]() Обчислити похідну функції y 5x2 1 3 x в точці х=1 x
Обчислити похідну функції y 5x2 1 3 x в точці х=1 x
2. Розв’язати диференціальне рівняння y''-7y'+6y=0, y(0)=5, y'(0)=3.
1. Дано еліпс 9x2+5y2=45. Знайти його півосі.
![]()
![]() А) a 3,b 5 Б) a 5,b 9 В) a 9,b 5 Г) a 5,b 3
А) a 3,b 5 Б) a 5,b 9 В) a 9,b 5 Г) a 5,b 3
2. Розв’язки характеристичного рівняння 1 і 2. Відповідне лінійне однорідне рівняння має вигляд:
А) y y 2y 0 Б) y 3y 2y 0 В) y 3y 2y 0
![]()
![]() 6 0 0
6 0 0
3. Обчислити визначник: 2 1 0
3 2 1
А) 7 Б) -7 В) 6 Г) -6
4. 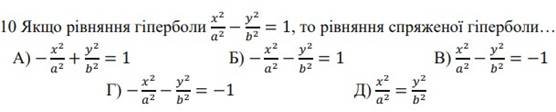
5. Знайти значення похідної функції f (x) x2 xcosx в точці x0 0
А) -1 Б) 0 В) 1 Г) 2
6. Знайдіть розв’язок рівняння y 2y 5y 0.
А) y C1ex C2ex Б) y (C1ex C2ex)cos2x В) y ex(C1 cos2x C2 sin2x) Г) y C1e5x C2e2x
Завдання 2
xdx
1. Обчислити інтеграл ![]() 32x2
32x2
2. Задано трикутник ABC : A(1, −1), B(−2, 1), C(3, 5). Скласти рівняння перпендикуляра, який опущений з вершини A
1. Дано пряму 5x+3y-3=0. Визначити кутовий коефіцієнт прямої паралельної даній:
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
2. Знайти f (x) x2 4x , де x 21 10
7 5 12 0 12 0 7 5
А) 0 10 Б) 7 5 В) 7 5 Г) 0 10
3. 
4. Загальне рішення однорідного диференціального рівняння 2-го порядку має вигляд y C1x C2e6x. Визначити корені характеристичного рівняння А) 1; 6 Б) -6; 0 В) 6; 6 Г) -6; -6
5. З даних рівнянь вибрати рівняння еліпса із центром на початку координат і півосями а=4 і b=5
![]()
![]() А) x2 y2 1 Б) x2 y2 1 В) 16x2 25y2 400 Г) 25x2 16y2 400
А) x2 y2 1 Б) x2 y2 1 В) 16x2 25y2 400 Г) 25x2 16y2 400
25 16 25 16
6. Знайти похідну функції y 4x2 2x 7
А) 8x+9 Б) 4x+2 В) 8x+2 Г) 8x
Завдання 2
3x2dx
1. Обчислити інтеграл ![]() (15x3)3
(15x3)3
![]()
![]() 1 2 3 4
1 2 3 4
2. Обчислити визначник: 2 3 4 1
3 4 1 2
4 1 2 3
1. Якщо дві прямі паралельні, то їх коефіцієнти задовольняють формулі:
А) k1 k2 Б) k1 k2 1 В) k1 k2 1 Г) k1 k2 1
![]()
![]() 1 0 0
1 0 0
2. Обчислити визначник: 2 3 4
1 1 2
А) -2 Б) 2 в) 1 Г) 0
3. 
4. Знайти значення похідної функції f (x) sin4 x cos4 x в точці x0 ![]()
2
А) 2 Б) 1 В) 0,5 Г) 0
![]() 3
3
5. Обчислити інтеграл 0 cos2 xdx
![]()
![]()
![]()
![]() А) 5 3 Б) В) 5 3 Г)
А) 5 3 Б) В) 5 3 Г)
6. Диференційному рівнянню y 3y 0 відповідає характеристичне рівняння:
А) k2 3k 0 Б) k2 3k 0 В) k2 3 0 Г) k2 3 0
Завдання 2
3cosxdx
1. ![]() Обчислити інтеграл 1 2sin x
Обчислити інтеграл 1 2sin x
2. Дано еліпс 9x2+5y2=45. Знайти його ексцентриситет.


про публікацію авторської розробки
Додати розробку

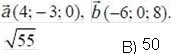 Дано вектори Знайдіть
Дано вектори Знайдіть