Підсумковий урок з теми «Арифметичний квадратний корінь з числа та його властивості. Перетворення ірраціональних виразів»
Тема. Підсумковий урок з теми «Арифметичний квадратний корінь з числа та його властивості. Перетворення ірраціональних виразів»
Мета: повторити, узагальнити та систематизувати знання та вміння учнів щодо означення, властивостей арифметичного квадратного кореня з числа та способів його застосування для перетворення числових та буквених виразів.
Тип уроку: систематизація та узагальнення знань і вмінь.
Наочність та обладнання: опорні конспекти.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Засвоєння учнями матеріалу, вивченого на попередньому уроці, перевіряємо під час тестової роботи.
Тестова робота 9
Функція ![]() , її графік та властивості
, її графік та властивості
-
Функцію задано формулою
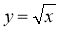 . При якому значенні аргументу значення функції дорівнює 4?
. При якому значенні аргументу значення функції дорівнює 4?
|
А |
Б |
В |
Г |
|
2 |
-2 |
16 |
-16 |
- Укажіть неправильне твердження.
А. Область визначення функції ![]() — множина невід'ємних чисел.
— множина невід'ємних чисел.
Б. Графіком функції ![]() є вітка параболи.
є вітка параболи.
В. Точка (16; 4) належить графіку функції ![]() .
.
Г. Пряма у = -3 перетинає графік функції ![]() .
.
-
Графік функції
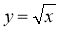 перетинає пряму у = 9. Знайдіть координати точки перетину.
перетинає пряму у = 9. Знайдіть координати точки перетину.
|
А |
Б |
В |
Г |
|
(9; 81) |
(81; 9) |
(3; 9) |
(9; 3) |
- Визначте рівняння, розв'язання якого зображено на рисунку
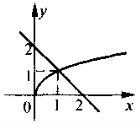
|
А |
Б |
В |
Г |
|
|
|
|
|
III. Формулювання мети і завдань уроку, мотивація навчальної діяльності учнів
Основна дидактична мета та завдання на урок цілком логічно випливають з місця уроку в темі — оскільки урок є останнім, підсумковим, то важливим є питання повторення, узагальнення та систематизації знань та вмінь, набутих учнями в ході вивчення теми. Таке формулювання мети створює відповідну мотивацію діяльності учнів.
IV. Повторення та систематизація знань
Залежно від рівня підготовки учнів, їх роботу вчитель може організувати різними способами: або як самостійну роботу з теоретичним матеріалом (наприклад, за підручником або за конспектом теоретичного матеріалу повторити зміст основних понять теми, або ж скласти схему, що відображає логічний зв'язок між основними поняттями теми, тощо), або традиційно провести опитування (у формі інтерактивної вправи) за основними питаннями теми (див. усні вправи).
Виконання усних вправ
- Сформулюйте означення АКК.
-
Чому дорівнює
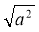 ?
?
-
При яких значеннях а має корені рівняння х2 = а?
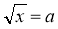 ?
?
- Чому дорівнює квадратний корінь із степеня а2п, де а ≥ 0?
-
На прикладі
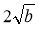 покажіть, як можна внести множник під знак кореня.
покажіть, як можна внести множник під знак кореня.
-
На прикладі виразу
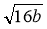 покажіть, як можна винести множник з-під знака кореня.
покажіть, як можна винести множник з-під знака кореня.
-
На прикладі виразів
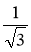 і
і 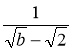 покажіть, як можна звільнитись від ірраціональності в знаменнику дробу.
покажіть, як можна звільнитись від ірраціональності в знаменнику дробу.
V. Повторення та систематизація вмінь
Зазвичай цей етап уроку проводиться у формі групової роботи, мета якої полягає у тому, щоб учні самі сформулювали та випробували узагальнену схему дій, якої вони мають дотримуватись під час розв'язування типових завдань, подібні до яких будуть винесені на контрольну роботу. Наприклад, типовими завданнями теми «Арифметичний квадратний корінь та його властивості. Перетворення ірраціональних виразів» є завдання:
- Обчислити значення числового виразу із застосуванням означення арифметичного квадратного кореня.
- Обчислити значення числового виразу із застосуванням властивостей арифметичного квадратного кореня (корінь з добутку, частки, степеня, а також добуток, частка і степінь арифметичних квадратних коренів).
- Довести, що дане число є раціональним (або ірраціональним).
- Розв'язати рівняння виду х2 = а, а також рівнянь, що зводяться до такого саме вигляду.
- Винести числовий (буквений) множник з-під знака кореня.
- Внести числовий (буквений). множник під знак кореня.
- Виконати тотожні перетворення числових та буквених ірраціональних виразів із застосуванням вивчених алгоритмів.
-
Побудувати графік функції
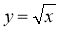 та виконати найпростіші вправи на читання побудованого графіка.
та виконати найпростіші вправи на читання побудованого графіка.
Після складання списку основних видів завдань учитель об'єднує: робочі групи учнів (за кількістю видів завдань) і завдання кожної з груп формулюється як '«Скласти алгоритм розв'язання завдання...» (кожна група отримує індивідуальне завдання). На складання алгоритму кожній групі відводиться певний час, за який учні мають скласти алгоритм, записати його у вигляді послідовних кроків, підготувати презентацію своєї роботи. По закінченні відбувається презентація виконаної роботи кожною групою. Після виступів обов'язкове випробування алгоритмів: причому бажано, щоб групи обмінялись алгоритмами і перевірили їх застосування не на одному, а на кількох завданнях. Після випробування — обов'язкова корекція та підбиття підсумків.
VI. Підсумки уроку
Підсумком уроку узагальнення та систематизації знань і вмінь учнів є, по-перше, складені самими учнями узагальнені схеми дій у ході розв'язування типових завдань, по-друге — здійснення учнями необхідної частини свідомої розумової діяльності — рефлексії відображення кожним учнем власного сприйняття успіхів, та найголовніше — проблем, над якими слід ще попрацювати.
VII. Домашнє завдання
- Вивчити складені на уроці алгоритми.
- Використовуючи складені алгоритми, виконати завдання домашньої контрольної роботи.
Домашня контрольна робота
- Знайдіть значення виразу:
а) ![]() ; б)
; б) ![]() ; в)
; в) 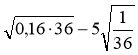 .
.
-
Обчисліть значення виразу, використавши властивості АКК:
а)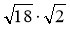 ; б)
; б) 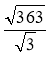 ; в)
; в) 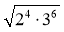 .
.
-
Розв'яжіть рівняння: а)
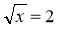 ; б) х2 = 5; в) х2 = -3; г)
; б) х2 = 5; в) х2 = -3; г) 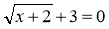 ;
;
д) ![]() ; є) (2х – 3)2 = 9.
; є) (2х – 3)2 = 9.
-
Графічно розв'яжіть рівняння: а) х2 = 2х – 1; б)
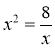 ; в) х2 = 5.
; в) х2 = 5.
-
Спростіть вираз: а)
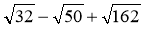 ; б)
; б) 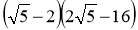 ;
;
в) ![]() ; г)
; г) 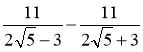 ; д)
; д) 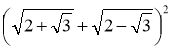 .
.
-
Скоротіть дріб:
а)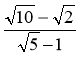 ; б)
; б) 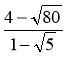 ; в)
; в) 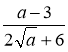 ; г)
; г) 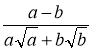 , а > 0, b > 0.
, а > 0, b > 0.


про публікацію авторської розробки
Додати розробку
