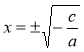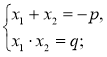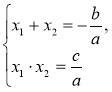Означення квадратного рівняння. Неповні квадратні рівняння та їх розв'язування

Тема. Означення квадратного рівняння. Неповні квадратні рівняння та їх розв'язування

Мета: домогтися свідомого розуміння учнями означення квадрат­ного рівняння, зведеного квадратного рівняння, неповного квадратно­го рівняння, назви коефіцієнтів квадратного рівняння; сформувати первинні вміння формулювати означення квадратного рівняння та його видів (зведеного та неповного), визначати коефіцієнти квадрат­ного рівняння та за ними визначати вид квадратного рівняння; підго­тувати учнів до сприйняття наступного матеріалу (розв'язування не­повних квадратних рівнянь).

Тип уроку: засвоєння знань та вмінь.

Наочність та обладнання: опорний конспект «Квадратні рівняння».

Хід уроку

І. Організаційний етап

На цьому етапі уроку слід надати учням інформацію про:

• орієнтовний план вивчення розділу;
• кількість навчальних годин;
• приблизний зміст матеріалу;
• основні вимоги до знань та вмінь учнів;
• орієнтовний зміст завдань, що будуть винесені на контрольну роботу.

(Цю інформацію можна помістити на стенді «Довідково-інфор­маційний куточок» у кабінеті математики та запропонувати учням для самостійного ознайомлення в позаурочний час).

II. Перевірка домашнього завдання

Якщо аналіз контрольної роботи учні виконували в письмовій формі, вчитель збирає зошити на перевірку.

III. Формулювання мети і завдань уроку

З метою усвідомлення учнями логіки вивчення матеріалу, пропо­нуємо їм схему, що відтворює основні змістові лінії шкільного курсу алгебри та зв'язок між ними:

Підставивши в цю схему ірраціональне число та узагальнивши ви­вчений матеріал, доходимо до висновку, що після ознайомлення із ви­дами і способами перетворень виразів, які містять квадратний корінь, слід перейти до вивчення всіх видів рівнянь (крім вивчених раніше рівнянь х² = а і , розв'язування яких пов'язано з вивченими властивостями ірраціональних виразів. Таким чином формулюється основна мета уроку.

IV. Актуалізація опорних знань та вмінь

 З метою успішного сприйняття учнями навчального матеріалу уроку слід активізувати такі знання і вміння: поняття многочлена стандартного вигляду та його коефіцієнтів; виконання арифметичних дій з многочленами, виконання рівносильних перетворень рівнянь, виконання арифметичних дій із дійсними числами.

Виконання усних вправ

1. Подайте у вигляді многочлена вираз:

(х – 2)(2 + х); (х – 3)²; (у³ – у)∙у; (у – 1)(у + 2).

2. Чи рівносильні рівняння:

а) 3х – 2 = х + 3 і 2х – 5 = 0; б) 5х – 1 = 3х – х² і х² + 2х – 1 = 0;

в) 0,5х – 3 = 0 і х – 6 = 0; г) 5х² – 10х + 25 = 0 і х² – 2х + 5 = 0?

Обґрунтуйте відповіді.

3. Розв'яжіть рівняння:

а) у – 7 = 0; б) х + 0,5 = 0; в) 8х = 0; г) 2х – = 0; д) у + = 0;

е) а(а – 1) = 0; ж) ; з) х² – 4 = 0; и) 2х² + 8 = 0; к) х² – 3 = 0.

V. Засвоєння знань

План вивчення нового матеріалу

1. Означення квадратного рівняння. Коефіцієнти квадратного рів­няння.
2. Зведене квадратне рівняння.
3. Неповне квадратне рівняння. Види неповних квадратних рівнянь.

 Формулюючи означення квадратного рівняння (як рівняння виду

ах² + bх + с = 0,

де а ≠ 0), щоб попередити помилки у визна­ченні коефіцієнтів квадратного рівняння, важливо вказати учням на той факт, що:

• знаки «+» у записі лівої частини рівняння лише показують, що ліва частина рівняння є многочленом (тобто сумою одночленів). Тому коефіцієнти квадратного рівняння визначаються так само, як і коефі­цієнти многочлена стандартного вигляду (бажано поновити в пам'яті учнів ці знання під час розв'язування відповідних усних вправ на етапі актуалізації знань);
• усі коефіцієнти квадратного рівняння (крім а) можуть набувати будь-яких дійсних значень (в тому числі можуть бути нулем). Тому, щоб учні не мали проблем, сприймаючи поняття неповного квадрат­ного рівняння, на початку знайомства з поняттям квадратного рівняння слід запропонувати достатню кількість прикладів квадрат­них рівнянь, коефіцієнти яких набувають різних за знаком та видом значень.

Для розуміння означень видів квадратних рівнянь важливо, щоб учні засвоїли назви коефіцієнтів квадратного рівняння. Цьому сприяти­ме багаторазове повторення матеріалу під час виконання усних і письмових вправ.

Уявлення про види квадратних рівнянь формується за традицій­ною схемою. Ці види виділяються під час розгляду особливих випадків коефіцієнтів квадратного рівняння.

VI. Формування вмінь

Виконання усних вправ

1. Укажіть серед поданих рівнянь квадратні: а) 5х – 2 = 0;

б) х² – х + 1 = 0; в) ; г) ; д) х³ – х = 0; е) 5х² + х = 0.

Для квадратних рівнянь назвіть значення їх коефіцієнтів.

2. Серед рівнянь виберіть:

3х² – 2х + 7 = 0; ; х² – 9 = 0; 2х² + 7 – 5х² = 0; 6х² = 0; 3 – х² = 0.

а) зведені; б) неповні квадратні рівняння.

3. Запишіть рівняння у вигляді ах² + bх + с = 0 (якщо це можливо):

-5 – 2х + х¹² = 0; х² – 3 = 0; 5х – х² = 0.

Виконання письмових вправ

Для реалізації дидактичної мети уроку слід виконати завдання та­кого змісту:

1. Знаходження коефіцієнтів квадратною рівняння.

1) Заповніть таблицю:

2) Укажіть у квадратному рівнянні його коефіцієнти:

а) 5х² – 9х + 4 = 0; б) х² + 3х – 10 = 0; в) -х² – 8х + 1 = 0;

г) -4х² + 5х = 0; д) 6х² – 30 = 0; є) 9х² = 0.

2. Запис квадратного рівняння із заданими коефіцієнтами. Запишіть квадратне рівняння, коефіцієнти якого дорівнюють: а) а = 2; b = -3; с = 1; б) а = 3; b = 0; с = -7; в) а = -1; b = 4; с = 5; г) а = - 6; b = -2,4; с = 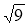;       д) а = 1; b = 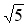; с = 0; є) а = 2; b = 0; с = 0.
3. Запис зведеного квадратного рівняння, рівносильного даному. Запишіть зведене квадратне рівняння, рівносильне даному:

а) 2х² + 2х – 6 = 0; б) -4х² – 10х + 8 = 0.

4. Зведення цілого рівняння до виду ах² + bх + с = 0 шляхом тотожних перетворень.

Зведіть рівняння до виду ах² + bх + с = 0:

a) (2x – 1)(2x + 1) = x(2x + 3); б) (3х + 2)² = (х + 2)(x – 3);

в) (х + 1)(х + 2) = (2х – 1)(x – 2); г) (х + 3)(3х – 2) = (4х + 5)(2х – 3).

5. На повторення: завдання, розв'язування яких передбачає виділення повного квадрата двочлена з квадратного тричлена.
6. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.

1) Порівняйте з нулем значення дробу (відповідь запишіть у вигляді нерівності): а) ; б) .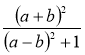

2) Видаліть зайвий запис: а) 3х² – 5x + 1 = 0; б) х² – 4х = 0;
в) (х – 1)² – (3х – 1)² = 0; г) (х – 1)² – (х + 2)² = 0.

 Мета перших 4-х видів письмових завдань (див. вище) — до­могтися засвоєння учнями означення квадратного рівняння та його різновидів, сформувати в учнів уміння правильно назива­ти та визначати коефіцієнти квадратного рівняння, а також по­вторити види рівносильних перетворень рівнянь та поновити в пам'яті способи дій під час виконання цих перетворень. Зав­дання на повторення мають на меті підготувати учнів до сприй­няття ними матеріалу наступного розділу «Формула коренів квадратного рівняння».

VII. Підсумки уроку

В якому випадку правильно визначено коефіцієнти?

У рівнянні 5х + х² – 4 = 0 коефіцієнти a, b, c відповідно дорівнюють:

а) 1; 5; -4; б) 5; 1;-4; в) -4; 5; 1; г) 1; -4; 5.

VIII. Домашнє завдання

1. Вивчити зміст теоретичного матеріалу уроку.
2. Розв'язати вправи на закріплення вивченого матеріалу (аналогіч­них за змістом до вправ класної роботи).
3. На повторення: вправи на виділення повного квадрата двочлена.