Піраміда. Різні випадки розміщення висоти в піраміді. 11 кл

Тема: Піраміда. Різні випадки розміщення висот в піраміді.

Мета: продовжити роботу над засвоєнням поняття піраміди та її елементів, над формуванням уміння учнів розв’язувати задач на знаходження величин елементів піраміди; доповнити знання учнів через ознайомлення з окремими випадками пірамід, а саме:

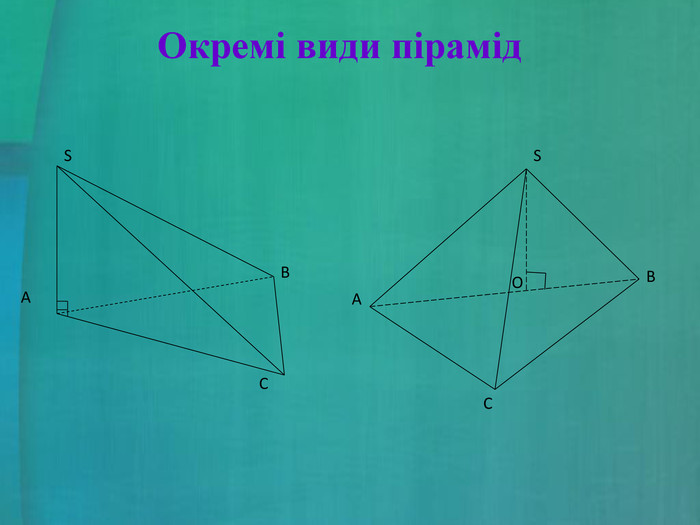
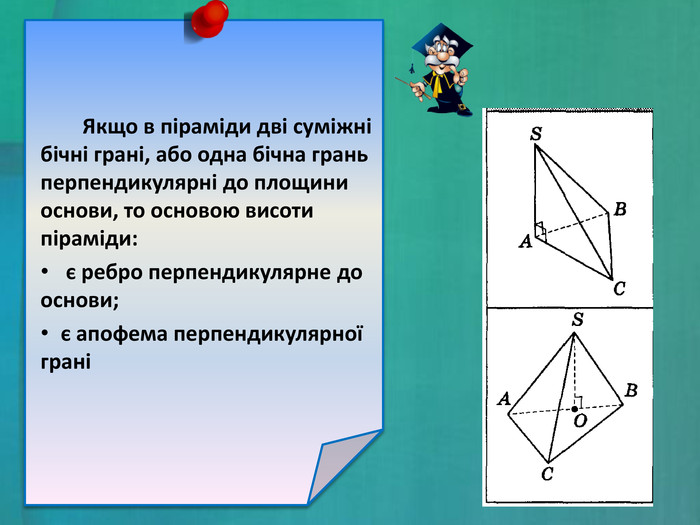
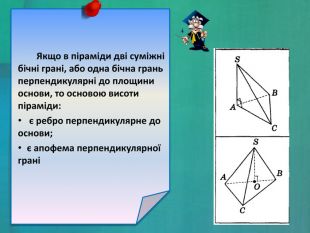
• пірамідами, в яких висота належить одній або двом бічним граням;
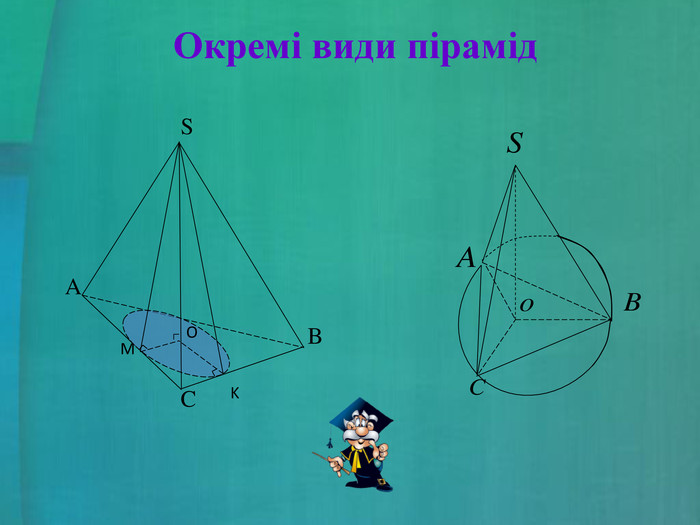
• пірамідами, в яких основою висоти є центр кола, описаного навколо основи піраміди;
• пірамідами, в яких основою висоти є центр кола, вписаного в основу піраміди.

Розвивати уяву, мислення.

Виховувати акуратність, самостійність, зацікавленість предметом.
 

Тип уроку: застосування знань, умінь і навичок.

Наочність та обладнання: мультимедійний проектор, ноутбук, ПК.

Хід уроку

І. Організаційний етап 

Перевірка готовності учнів до уроку, налаштування на роботу.

ІІ. Перевірка домашнього завдання

Перевірка якості виконання письмових вправ домашнього завдання проводимо у формі усних відповідей учнів по готовому рисунку на дошці. (слайд 2,3)

Перевірку засвоєння учнями теоретичного матеріалу проводимо у формі тестів на ПК або на індивідуальних картках (5 учнів).

1. Відрізки, які з'єднують вершину піраміди з вершинами її основи, називають (А - вершина, Б - апофема, В - бокові ребра, Г - грані)
2. Піраміда в основі якої лежить трикутник, називається ( А - октаедр, Б - тетраедр, В - куб, Г - чотирикутна піраміда)
3. Піраміда, в основі якої лежить правильний  n-кутник, а бічні ребра рівні між собою, називається ( А - правильна,Б - квадратна, В - довільна, Г - зрізана)
4. Геометричне тіло, відітнуте від піраміди площиною, яка паралельна основі, називається ( А - правильна піраміда, Б - квадратна піраміда,В -  довільна піраміда, Г - зрізана піраміда)
5. Площа бокової поверхні піраміди дорівнює сумі площ її (А – двох любих граней, Б – бокових ребер, В – всіх граней, Г – бокових граней)
6. Апофемою піраміди називається висота (А – бокової грані, б – піраміди, В – основи піраміди, Г – проведеної до любого ребра)
7. Піраміда це (А - многогранник, у яого шість граней, і всі вони рівні квадрати, Б - многогранник, у якого шість граней, і кожна з них паралелограм, В - мноогранник, одна грань якого довільний многокутник, а інші грані трикутники, Г - множинв всіх точок простору рівновіддалених від даної точки)
8.  Скільки граней у чотирикутної піраміди? ( А – 4, Б – 5, В – 6, Г – 7).
9. Скільки ребер у тетраедра? ( А – 6, Б – 7, В – 8, Г – 9)
10.      Чи може мати піраміда 45 ребер? (А – так, Б – ні)
11.      Чи може мати піраміда 44 грані? ( А – ні, Б - так)

ІІІ. Актуалізація опорних знань

Фронтальне опитування

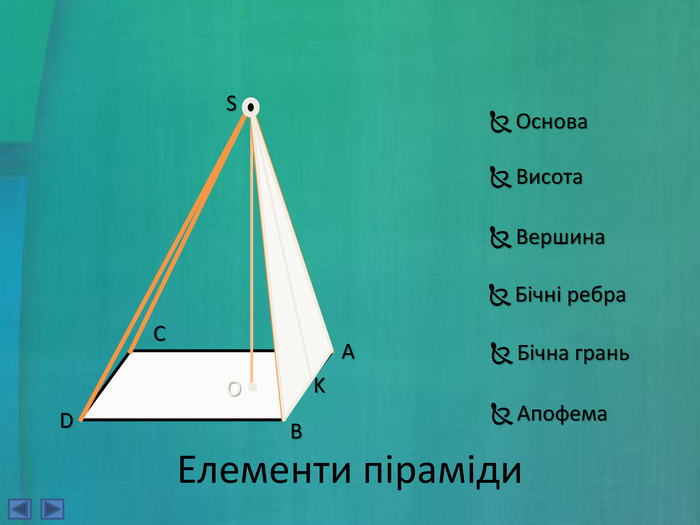
1. Сформулюйте означення елементів піраміди (слайд 4).
2. Сформулюйте теорему про три перпендикуляри (слайд 5).
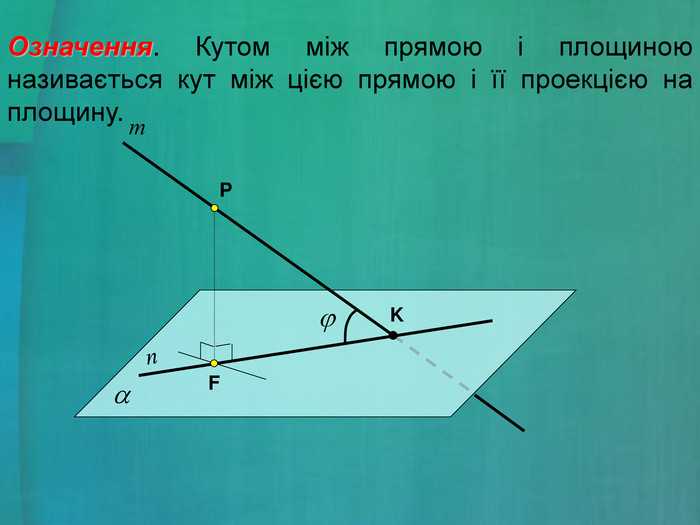
3. Сформулюйте означення кута між прямою та площиною (слайд 6).
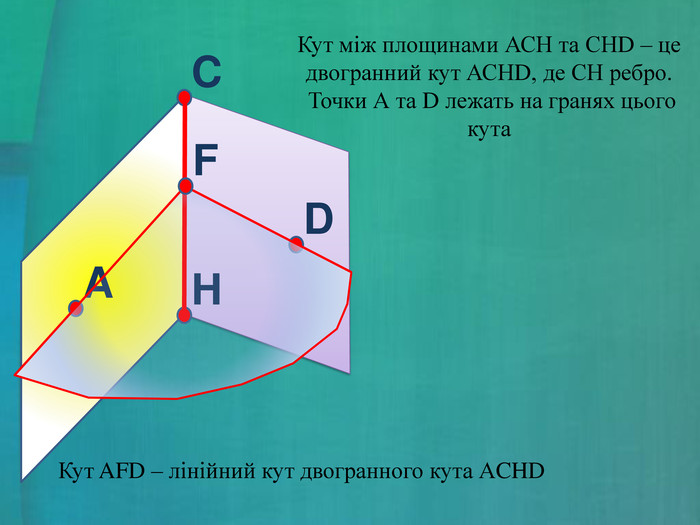
4. Сформулюйте означення кута між площинами (слайд 7).
5. Які ви знаєте способи побудови лінійного кута двогранного кута (слайд 8)
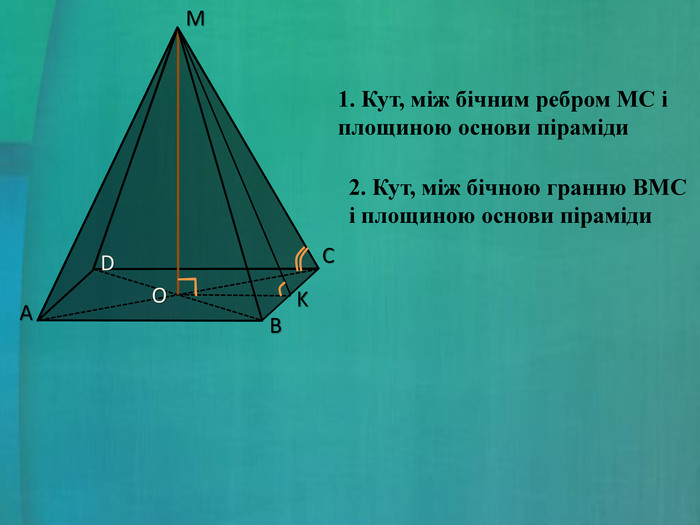
6. Вкажіть кут, між бічним ребром МС і площиною основи піраміди (слайд 9).
7.  Вкажіть кут, між бічною гранню ВМС і площиною основи піраміди (слайд 9)
8. Як побудувати чотирикутну піраміду? (слайд 10)

ІV. Формування мети й завдань уроку

Для створення відповідної мотивації роботи можна запропонувати задачу. (слайд 11)

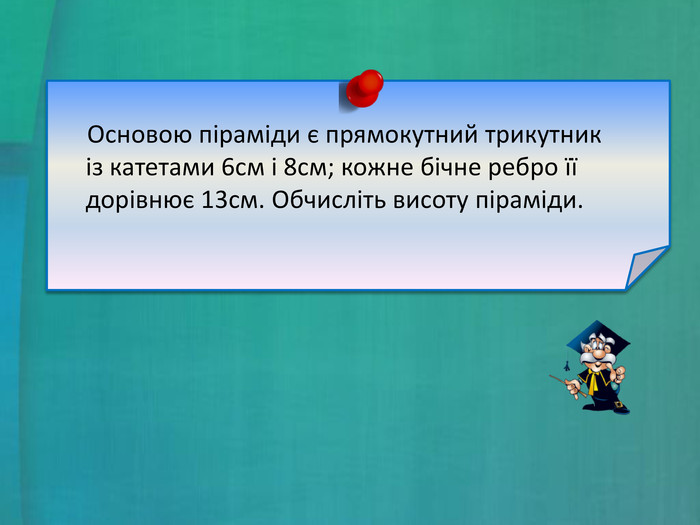
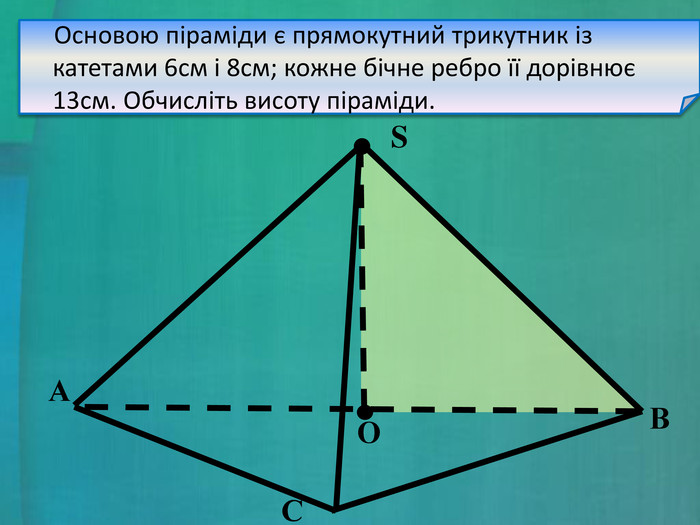
Задача. Основою піраміди є прямокутний трикутник із катетами 6см і 8см; кожне бічне ребро її дорівнює 13см. Обчисліть висоту піраміди.

Для того щоб знайти довжину висоти піраміди, необхідно її побудувати. Виникає питання: де лежить основа висоти піраміди, якщо це не обумовлено в умові задачі? (слайд 12) Отже, завданням уроку є вивчення окремих випадків піраміди з метою в положення висоти (або основи висоти) піраміди (слайд 13).

V. Доповнення знань

1. Перегляд відеоролика з різними випадками розміщення висот в піраміді. Розв’язання стереометричних задач на піраміди зазвичай розпочинається з побудови рисунка. У багатьох випадках для правильного відображення на рисунку положення висоти піраміди необхідно провести попередній аналіз умови задачі, з’ясувати, які властивості має піраміда. 

2. Аналіз почутого і побаченого під час перегляду і визначення кількості випадків розміщення висот в піраміді. Визначення властивостей кожного виду пірамід (слайд 14, 15).

3. Узагальнення властивостей і визначення умов від яких залежить розміщення основи висоти піраміди (слайд 16,17,18)

4. Учням роздаються індивідуальні опорні конспекти на яких відображені окремі випадки пірамід і умови від яких залежить розміщення висот цих пірамід.

VІ. Формування вмінь

Виконання усних вправ

1. Висота піраміди дорівнює 6 см, а всі бічні ребра рівні й дорівнюють 10см. Чому дорівнює радіус кола, описаного навколо основи піраміди? (слайд 19)
2. Висота піраміди дорівнює 5 см, а всі бічні грані нахилені до площини основи під кутом 45°. Чому дорівнює радіус кола, вписаного в основу піраміди? (слайд 20) 
3. Усі бічні ребра трикутної піраміди утворюють із площиною її основи рівні кути, а одна з бічних граней піраміди перпендикулярна до площини основи. Визначте вид трикутника, що лежить в основі піраміди (слайд 21).

Виконання усних вправ

1. Тепер ми можемо повернутися до задачі, яка викликала в нас проблеми  на початку уроку. Основою піраміди є прямокутний трикутник із катетами 6см і 8см; кожне бічне ребро її дорівнює 13см. Обчисліть висоту піраміди. (слайд 22)

• Аналіз умови задач визначення місця розташування основи висоти піраміди. Побудова піраміди учнями в зошитах
• Фронтальний аналіз розв’язку задачі і самостійний запис учнями в зошитах короткого розв’язку.

2. Робота в групах

Учні діляться на дві групи:

1. Отримують завдання із підручника  (І група №13*, ІІ група №14*). Після самостійної роботи з кожної групи вибирається по два учні. Один з низ виконує побудову піраміди, а інший з місця розказує хід розв’язання задачі.
2. Умови задач для груп відображені на дошці (слайд 24) учні самостійно їх розв’язують користуючись готовими малюнками до задач (слайд 25).

3. Скласти задачу по рисунку і розв’язати її (слайд 26).
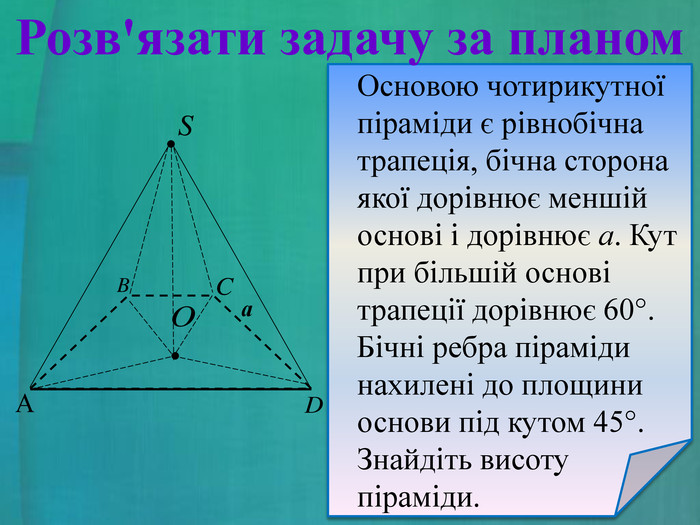
4. Розв’язати задачу за запропонованим планом по готовому рисунку (слайд 27).

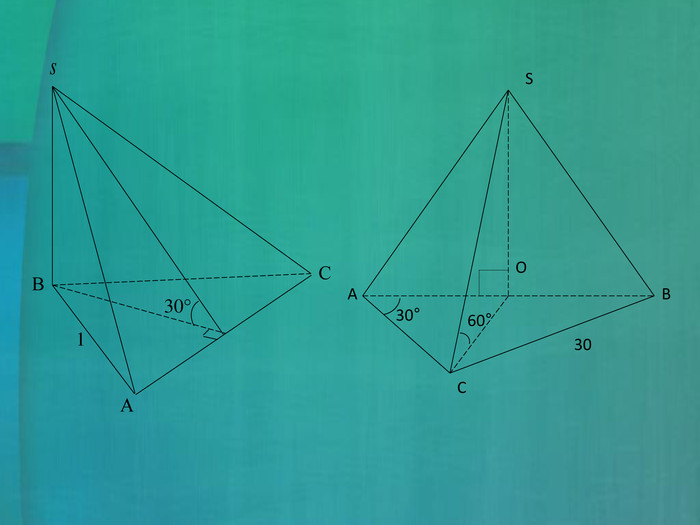
Задача. Основою чотирикутної піраміди є рівнобічна трапеція, бічна сторона якої дорівнює меншій основі і дорівнює а. Кут при більшій основі трапеції дорівнює 60°. Бічні ребра піраміди нахилені до площини основи під кутом 45°. Знайдіть висоту піраміди.

VІІ. Підсумки уроку

Контрольні запитання у формі тесту «Перевір себе» (слайд 28,29)

1. Яке найменше число граней може бути у піраміди?
2. Чи існує піраміда, яка має 125 ребер?
3. Чи існує піраміда, яка має 125 граней?
4. Чи може піраміда мати дві бічні грані, які перпендикулярні  до основи?
5. Чи може піраміда мати три бічні грані, які перпендикулярні до основи?
6. Піраміда може мати два бічні ребра перпендикулярні до основи?
7. Де знаходиться основа висоти піраміди, якщо в неї всі апофеми рівні?
8. Тетраедр – це піраміда?
9. Чи кожна  піраміда є тетраедром?
10.    Якщо одна з бічних граней піраміди перпендикулярна до основи, то висота піраміди збігається з висотою даної грані?

VІІІ. Домашнє завдання

(слайд 34) §16(ст.129), вивчити опорний конспект,

№14*,15 для всіх,   № 23* за бажанням

(слайд 35) Творче завдання: підготувати коротке повідомлення або презентацію по темам: «Історія пірамід на Землі»,

«Піраміди – правда і міфи»,

«Піраміди навколо нас»,

«Піраміди сучасності»