:«Площі бічної та повної поверхонь конуса»

                                                         Урок №___                          Дата 03.02.2021

Тема уроку:«Площі бічної та повної поверхонь конуса».

Тип уроку:урок викладу нових знань.

Вид уроку:урок-бесіда.

Формування компетентностей:

предметна компетентність:домогтися засвоєння формул для обчислення площ бічної та повної поверхонь конуса; сформувати вміння розв’язувати задачі, що передбачають застосування формул для обчислення площ бічної та повної поверхонь конуса;

ключові компетентності:

спілкування державною мовою – чітко, лаконічно та зрозуміло формулювати думку, аргументувати, доводити правильність тверджень;  

математична компетентність – оперуватичисловою інформацією,  геометричними об’єктами в просторі, розв’язувати задачі, зокрема практичного змісту;  

уміння вчитися впродовж життя – усвідомлювати цінність нових знань і вмінь для обраної професії;  

соціальна та громадянська компетентності – висловлювати власну думку, слухати й чути інших, співпрацювати в команді.

Методи та прийоми: евристичний,  спонукально-пошуковий, інтерактивний, демонстраційний.

Обладнання:

1. Роздатковий матеріал (підручники  Мерзляк  «Математика 11 клас»).
2.     Дошка (записано число, тема, рисунки до вправ);
3.     Мультимедійна презентація уроку;
4.     Індивідуальні картки з завданнями;
5.     Моделігеометричних тіл.

Міжпредметні зв’язки:  алгебра, креслення.

Структура уроку:

1. Організаційний момент.
2. Перевірка домашнього завдання.
3. Актуалізація опорних знань учнів.
4. Формування  нових знань, умінь та навичок.
5. Закріплення нового матеріалу.
6. Підведення підсумків уроку.
7. Домашнє завдання.

Хід уроку.

1. Організаційний  момент (рапорт, привітання, перевірка наявності  ручок, олівців, лінійок, зошитів).

Девіз уроку:

Не просто слухати, а чути.  

Не просто дивитися, а бачити.  

Не просто розмовляти, а діло творити 

Не просто відповідати, а міркувати, 

Дружно і плідно працювати.

2. Перевірка домашнього завдання.

        Перевіряю наявність письмової домашньої роботи в зошитах.

3. Актуалізація опорних знань учнів.

Сьогодні на уроці, ми продовжимо вивчати площі поверхонь  геометричних тіл і покажемо важливість теми у вашій професії.

1. записуємо в зошитах  тему уроку ;

2. мотивація навчальної діяльності:

Чи потрібно Вам, майбутнім кравцям, вивчати дану тему, чи знадобляться отримані на сьогоднішньому уроці знання в майбутньому? Для того, щоб відповісти на ці питання я пропоную вам подивитися фрагмент ізмультфільму(демонструєтьсяфрагмент із мультфільму «Жадный богач»).

Якщо ви уважно дивилися мультфільм, то могли переконатися, щопрактика без теорії неможлива, якби багач знав математику, то він би розрахував сам, скільки вийде шапок і не отримав би такого розчарування. Що не розрахував жадібний багач? (Скільки потрібно матеріалу на одну шапку, тобто, яка площа поверхні однієї шапки). Тому, щоб не потрапити в халепу, як багач, необхідно вивчити деякі теоретичні питання.

3. створення проблемної ситуації: 

Задача. Конусоподібну палаткувисотою 2,4 м і діаметром основи

1,4 м вкрито тканиною. Скільки квадратних метрів тканини пішло на палатку?(Слайд 19)

Відповідь можна надати швидко, якщо знати формули, із якими ви ознайомитися на уроці.

4. Формування  нових знань, умінь та навичок:

План вивчення теми:

1. Розгортка бічної поверхні конуса.
2. Формула для обчислення площі бічної поверхні конуса.
3. Формула для обчислення площіповної поверхні конуса.
4. Приклади застосування формул для обчислення площ бічної та повної поверхонь конуса. 

Що є розгорткою бічної поверхні конуса?(Круговий сектор).(Слайд 20)

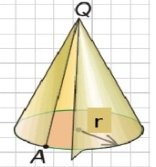
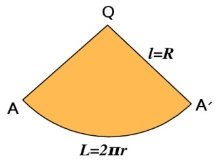
Чому дорівнює радіус цього кругового сектора? (Твірній конуса).

Чому дорівнює довжина дуги сектора? (Довжині кола  основи конуса).

Площею бічної поверхні конуса будемо вважатиплощу її розгортки.

Виразимо площу бічної поверхні конуса S_біч. через його твірну ℓ і радіус основи R.

Площа бічної поверхні конуса дорівнює добутку половини довжини кола основи на твірну.

Чому дорівнює довжина кола основи? (с = 2πR)

Тоді  S_біч. = πRℓ.

Що необхідно, щоб знайти площу повної поверхні конуса? (До площі бічної поверхні додати площу основи).(Слайд 21)

Маємо  S_п= S_біч + S_осн

Чому дорівнює площа основиконуса? (S_осн. = πR²).

Тоді   площа повної поверхні конусаS_п= πRℓ + πR²=πR(ℓ+R).

5. Закріплення нового матеріалу.

• Колективне розв’язування задач під керівництвом викладача

Повертаємося до практичної задачі, розглянутої на початку уроку, яка зводиться до знаходження площі бічної поверхні конуса.

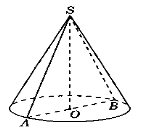Задача 1. Розв’язання: (учні розв’язують задачу за допомогою допоміжних питань).

Записуємо умову задачі.(Слайд 23)

Які елементи конуса вам відомі? (Висота та діаметр).

Що необхідно знайти? (Площу бічної поверхні).

За допомогою якої формули знайдемо площу бічної поверхні конуса?

(S_біч. = πRℓ).

Побудуйте малюнок. Записуємо формулу.

Чому дорівнює радіус конуса? (половині діаметра).(Слайд 24)

Як знайти твірну конуса? (за теоремою Піфагора).

Знайдіть твірну конуса.

Записуємо: Із трикутника SOA (SOA = 90°) отримаємо за теоремою Піфагора:

ℓ = SA = ℓ = =

Знайдіть бічну поверхню конуса.

Записуємо: тоді

Відповідь: 5,495

Задача 2. Знайдіть площу бічної поверхні  зрізаного конуса, у якого радіуси основ дорівнюють 5 см і 11 см, а кут між твірною і висотою 30.

Розв’язання задачі 2 (учні розв’язують самостійно за допомогою алгоритму, записаного на дошці; для учнів з достатнім рівнем навчальних досягнень пропоную картки з індивідуальними завданнями). (Слайд 25)

1. Запишіть коротко умову задачі.
2. Запишіть формулу для обчислення площі повної поверхні конуса.
3. Чому дорівнює кут між твірною та висотою конуса?
4. Знайдіть радіус конуса, використовуючи властивість прямокутного трикутника з кутом 30⁰ .
5. Знайдіть S_п.
6. Яким буде діаметр даного конуса?
7. Запишіть відповідь.

Перевірте:(Слайд 26)

Дано: ℓ = SA = 14 см; SAO=60°.  S_п-?

Розв’язок:S_п = πR(ℓ+R),

Із трикутника SOA : SOA = 90°, SAO =60° (за умовою), тоді ASO =30°, тобто R= = 14:2=7 см;тоді S_п = π ⋅7(14+7)=147π =147⋅3,14≈462см².АВ = d = 2R =14 см.

Відповідь:≈462 см², 14 см.

Індивідуальне завдання.

Задача. Уявіть, що ви є власником швейної фабрики. Вам повідомили, що до вас приїде перевірка, яка оглядатиме пожежні щити, а у вас не вистачає конусних відер, купити ніде, замовити часу не має, але є у вас лист заліза 2 м × 1,5 м і є робітник який знає зварювальну справу. Отже, перед вами постає задача.

Скільки можна виготовити конічних відер із цього листа? Якщо відомо, що діаметр відра становить 28 см, а висота – 39 см.

Розв’язування цієї задачі зводиться до знаходження площі бічної поверхні конуса.

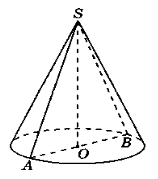Розв’язання:

АВ = d = 28 см, отже ОА = R = 14 см,  SO = H = 39 см.

Із трикутника SOA ( SOA = 90°) отримаємо за теоремою Піфагора:

ℓ = SA =

ℓ = =

Відомо, що тоді 

Площу листа можна обчислити за формулою площі прямокутника:

S_листа=  отже

S_листа= 200 · 150 = 30000 см².

Який висновок ми зможемо зробити? Скільки можна зробити відер?

       Відповідь: 16 відер.

Колективна робота.

Викладач разом із студентами розв’язує наступну задачу.

Молодій родині необхідно перекрити дах будинку. Дах має конічну форму : діаметр 8м і висота 3м. Один лист металочерепиці має розміри  0,6м x 1,2м і коштує 40 грн. Один лист бітумної черепиці має розміри 0,8м x 1,25м і коштує 45 грн. На шви та обрізку витрачається 10 % від площі даху. Визначити площу даху та яке покриття даху фінансово вигідніше родині.

При цьому, на певному етапі розв’язування задачі, викладач визиває до дошки студента-помічника і вже разом роблять розрахунки.

Відповідь:Площа даху дорівнює см², ціна покрівлі з металочерепиці дорівнює 3840 грн., а з бітумної черепиці – 3150 грн. Отже, фінансово вигідніше перекрити дах будинку бітумною черепицею.

6. Підведення підсумків уроку

Питання до учнів:

1. З чого складається бічна поверхня конуса? Як позначається?
2. За якою формулою можна обчислити бічну поверхню конуса?
3. З чого складається повна поверхня конуса? Як позначається?
4. За якою формулою можна обчислити повну поверхню конуса?

Оцінювання учнів.

7. Домашнє завдання

1)    «Математика 11 клас»  Мерзляк

                            § 21   ст.191.

                                        2)    Розв’язати завдання на картках.

                                        3) Вивчити формули.