"Початки теорії ймовірностей"

Урок-проект з  алгебри та початків аналізу, 11 клас.

Тема.

Початки теорії ймовірностей.

Навчальна мета.

Продовжувати формувати знання учнів з основ теорії ймовірності. Вдосконалювати вміння учнів обчислювати ймовірності подій, продовжувати формувати вміння користуватись теоремами про суму подій та добуток подій при розв’язуванні задач, узагальнити знання учнів по темі.

Розвивальна мета.

Виховувати в учнів прагнення до самовдосконалення, інтерес до предметів, творчий підхід до дорученої справи, бачення перспективи та вміння робити правильні висновки.

Виховна мета.

Виховувати комунікативну компетентність, ініціативність, почуття естетичної досконалості та творчої самореалізації. Формувати уявлення про психологічні аспекти залежності від ігроманії.

Обладнання.

Гральні кубики, гральні карти, жетони, таблиця «Основні правила ймовірностей», пам’ятка-алгоритм для розв’язування задач, рулетка, монети, гра «Дартс».

ІКТ-супровід.

Мультимедійна дошка, середовище Publisher, ПЗ «DG»

Девіз.

О, сколько нам открытий чудных

Готовит просвещенья дух,

И опыт, сын ошибок трудных,

И гений- парадоксов друг,

И случай, бог-изобретатель…

А. С. Пушкин

Тип уроку.

Урок узагальнення і систематизації знань.

Форма проведення. Математичне казино.

Підготовча робота.

Клас об’єднався в 5 груп, які працювали над такими питаннями проекту:

1. Розв’язування задач № 1-24 на обчислення ймовірності подій;
2. Теоретичні питання № 1-20, що передбачають знання основних понять та теорем теорії ймовірностей;
3. Антиреклами гральному бізнесу;
4. Презентація навчальних посібників по даному розділу :
   • «Основні формули теорії ймовірностей»
   • «Термінологічний довідник теорії ймовірностей»
   • «Довідник історичних фактів з теорії ймовірностей»
   • «Дослідники в області теорії ймовірностей»
   • «Задачі ДПА та ЗНО з теорії ймовірностей»

Стислий опис проекту.

 Проект передбачає вивчення теорії ймовірності шкільного курсу шляхом самостійного творчого пошуку та заглиблення в тему на основі індивідуального досвіду та додаткової роботи з довідковою літературою учнів 11 класу спільно універсальної та профільної груп. Проект включає елементи дослідницького та інформаційного пошуку. Учням пропонується дати відповідь на питання доцільності ігроманії з урахуванням особистісного життєвого досвіду та отриманих навичок обчислення ймовірності масових подій. Учні повинні також засобами інформаційних технологій (Інтернет, журнали, посібники, телебачення) підготувати навчальні посібники для вивчення курсу теорії ймовірності, а також скласти антирекламу гральному бізнесу.

Навчальні предмети: алгебра, інформатика, історія, психологія.

 

Етапи проекту

Етапи проекту	Форми діяльності	Відповідальні
Мотивація	Повідомлення	Вчитель
Об’єднання учнів у групи, дотримання принципу комфортності членів	Вільний вибір та диференціація	Учні, вчитель
Пошук інформації, дослідницька діяльність	Самостійна робота, індивідуально-групова	Учні
Підбір системи задач		Вчитель
Оформлення проекту	Групова	Учні
Захист проекту	Колективна	Учні, вчитель
Оцінювання	Колективна та індивідуальна	Учні, вчитель, спостерігачі

Очікувані результати для учнів:

• Знаходити та опрацьовувати інформацію з використанням Інтернету та інших джерел;
• Працювати в групі для досягнення поставленої мети;
• Навчитися розв’язувати типові задачі т. й.
• Вивчити основні поняття та теореми т. й.;
• Зрозуміти, що гральний бізнес не може бути використаний для збагачення людини.

Оцінювання звітів груп:

1. Вміння та правильність розв’язування отриманих групою задач;
2. Зміст, влучність та доказовість антиреклами, переконливість що має бути побудована за принципом «практичної неможливості малоймовірних подій» - якщо випадкова подія має малу ймовірність, то при одиничних випробуваннях вона не настане;
3. Під час презентації публікацій: завершеність, повнота, зрозумілість викладеного матеріалу, оригінальність та різноманітність оформлення, грамотність, новизна;
4. Злагодженість роботи групи, максимальна участь всіх членів у звіті

Порядок звітів груп

Учні сидять за столиками спеціального оформлення за власним бажанням: скатертина, емблема, одяг учасників. За жеребом до круглого столу в центрі виходить група і обирає з допомогою вовчка один із залів «математичного казино» відповідно до символів:

• Гральний кубик – задачі на обчислення ймовірності випробування «кинуто гральний кубик»;
• Гральна карта – задачі на обчислення ймовірності випробування «витягнули карту»;
• Лотерейний білет – задачі на обчислення ймовірності випробування «куплено лотерейний білет»;
• Цукерка – задачі на обчислення ймовірності випробування пов’язані із харчовими продуктами;
• Монета – задачі на обчислення ймовірності випробування «кинули монету»
• Мішень – задачі на обчислення ймовірності випробування «зроблено постріл».

Захист проекту

Вчитель. Друзі! Сьогодні у нас значна подія – 5 фірм-видавництв «Монетка», «Яблучко», «Рулетка», «Козирна карта» та «Гральні кубики» випустили з друку 5 книг, які сьогодні і будуть презентовані гостям. Та перш ніж це відбудеться вони мають нагоду відвідати математичне казино, де зможуть обміняти свої міцні знання на тверді оцінки. Тож нагадую, що в залах нашого казино слід демонструвати свої знання з теорії ймовірності і хай фортуна буде вашою супутницею, а слова О. С. Пушкіна (звучить девіз) додадуть оптимізму гравцям. Мета нашого проекту може бути сформульована дієсловами – повторити, розв’язати, узагальнити, систематизувати, переконати, досягнути, самовдосконалитись, реалізувати. Почнемо з важливого – антиреклами грального бізнесу, переконаємо присутніх, що знання з теорії ймовірності дають нам можливість скептично ставитись до сумнівних виграшів.

• Кожна група демонструє антирекламу до одного із видів грального бізнесу:
  • Група №1 «Монетка» (демонструє гральний апарат «Гроші сюди»та показавши його дію, доводить, що гральні автомати не є чесною грою)
  • Група №2 «Яблучко» (розглядає задачу, у якій ставлять ставки на влучення гравцем у ціль, при цьому ймовірність отримується мала, а отже, за формулою Бернуллі, бажана подія не настає)
  • Група №3 «Рулетка» ( демонструє рулетку, у якій роблять ставку на число та колір і доводить, що при одиничному випробуванні подія не настає)
  • Група № 4 «Козирна карта» (доводить за допомогою демонстраційних карт, що ймовірність виграшу мала)
  • Група №5 «Гральні кубики» (демонструють два кубики на одному прізвища учасників, а на другому – їх фото, доводять, що при одночасному підкиданні кубиків спів падання прізвища і фото не відбувається)

Вчитель. Пропоную членам видавничих фірм пройти до гральних залів. Вам дається можливість відчинити лише одні двері, за якими знаходяться навчальні ігри з круп’є (вчитель), вигравши ви зможете отримати жетони різного номіналу, які і обміняєте на оцінки в кінці уроку. Та щоб зайти до залу слід мати знання, тому кожен витягне питання і відповість на нього, переконавши нас, що має знання. При цьому кожна група виходить до центрального столу та представляє назву своєї видавничої фірми, члени команди обирають запитання методом випадкових чисел.

1. Що вивчає теорія ймовірностей?
2. Назвати основні поняття теорії ймовірностей.
3. Який дослід вважають стохастичним?
4. Що таке подія?
5. Що таке випробування?
6. Яку подію називають неможливою?
7. Яку подію називають вірогідною?
8. Яку подію називають випадковою?
9. Які події називають масовими?
10. Що таке повна група подій?
11. Які події називають сумісними в даному випробуванні?
12. Які події називають попарно несумісні?
13. Що таке рівноможливі події?
14. Що називають імовірністю випадкової події?
15. Чому дорівнює імовірність випадкової події?
16. Чому дорівнює імовірність неможливої події?
17. Яку умову задовольняє імовірність випадкової події?
18. Які події називаються протилежними?
19. Які події називаються залежними?
20. Які події називають складеними?

Учні витягують запитання і відповідають на них, отримавши за відповідь фішки трьох кольорів (в залежності від складності запитання).

• Кожна група сідає за стіл і розв’язує вибрані задачі (див. додаток «Типові задачі до уроку-проекту»). Кожен має право отримати підказку до задачі. Задачі учні обирають відповідно до рівня навчальних досягнень: в –високий, д – достатній, с – середній, п – початковий.

 

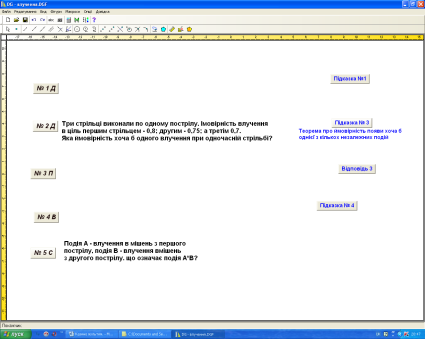
Наприклад, дивись рисунок. Середовище DG - питання як і підказка сховані під кнопку.

Учень за бажанням вибирає задачу і при необхідності може скористатись підказкою, але втративши при цьому певну кількість балів.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

• Кожна група демонструє з допомогою інтерактивної дошки власні публікації, представляючи видавничу фірму

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приклад оформлення одного із посібників

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

• Оцінювання проектів
• Дати відповіді на запитання:

 

 

1. Чи допоміг вам сьогоднішній урок краще усвідомити тему?
2. Розвитку яких рис характеру сприяв урок? (Самостійності, спостережливості, відповідальності, тощо).
3. Які пізнавальні процеси були задіяні на уроці найбільше? (Мислення, пам'ять, увага, уява інше).
4. Який життєвий досвід ви набули? (Володіти собою, захищати свої знання, бути впевненими в собі, вести себе в незвичних умовах.)
5. Чи отримали ви задоволення від власної праці? Чи вичерпали ви свої можливості? Чи є бажання повторити сьогоднішні відчуття?
6. Чим ви незадоволені? Що було недоцільним? Що слід виправити?
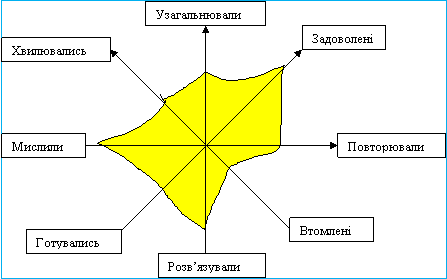
7. Охарактеризуйте свій емоційний стан протягом уроку (хвилювались, боялись, дивувались, зосереджувались, інш.) та в кінці уроку (задоволення, виснаження, успіх, впевненість, радість, інш.).
8. Поставте самооцінку та оцініть роботу своєї групи.

 

 

 

 

Типові задачі до уроку-проекту

1.  (с) Чи утворюють повну групу подій у випробуванні «кидання грального кубика» такі події:
   • А – поява парного числа, В – поява непарного числа;
   • А – поява простого числа, В – поява складеного числа.
2. ( п) Подія А – поява 3 очок у результаті кидання грального кубика. Чому дорівнює ймовірність появи протилежної події?
3. (д) Гральний кубик кидають тричі. Знайти ймовірність того, що за три кидки випаде 6 очок рівно один раз.
4. (в) Гральний кубик кинули 8 разів. Знайдіть імовірність того, що 4 очки випадуть не менше ніж один раз.
5. (с) Випробування – витягування однієї карти з колоди. А – поява «10», В – поява «6». Що означають події А+В, А*В? Чи є вони випадковими, неможливими або вірогідними?
6. (д) З колоди у 36 карт навмання витягують три карти. Яка ймовірність того, що вибрані карти дами?
7. (п) В урні лежать 2 чорних, 3 червоних, 9 зелених і 6 синіх кульок. Яка ймовірність того, що вона не чорна?
8. (д) В урні міститься 12 кульок: 5 білих і 7 чорних. Навмання виймають 3 кульки. Яка ймовірність того, що серед вийнятих кульок усі 3 чорні?
9. (в) У скрині лежать 6 білих, 4 чорних і 3 синіх кулі. Зі скрині навмання виймають 2 кулі. Яка ймовірність того, що кулі будуть або обидві білими, або обидві чорними?
10. (в) В урну, у якій є дві кульки, поклали кульку білого кольору, після чого з урни навмання витягують одну кульку. Знайди ймовірність того, що витягнута кулька буде білого кольору, якщо рівно можливі всілякі припущення про колір кульок, які були в урні.
11. (д) Яка ймовірність того, що з 10 куплених лотерейних білетів буде два виграшних, якщо ймовірність одержати виграшний білет дорівнює 0,2?
12. (с) із 10000 тисяч квитків лотереї 10 виграють по 200 гривень, 100 – по 100 гривень, 500- по 25 гривень. Громадянин придбав один квиток. Яка ймовірність виграшу не менше 100 гривень?
13. (с) Готуючись до заліку учень із 15 запитань вивчив 5. Яка ймовірність того, щ о із 3 навмання заданих йому запитань він відповість  хоча б на одне?
14. (в) В лото «Забава» необхідно вгадати 6 цифр із 9. Яка ймовірність виграти?
15. (д) Імовірність того, що бутерброд упаде маслом догори 0,2. Яка ймовірність того, що при 10 падіннях бутерброду він упаде маслом догори рівно 4 рази?
16. (с) На тарілці лежать 15 цукерок «Білочка», 25 цукерок «Ромашка» і 30 цукерок «Політ». Ви навмання берете підряд 3 цукерки. Яка ймовірність того, що першого разу витягнете «Білочку», другого – «Ромашку», а третього «Політ»?
17. (в) Ресторан замовляє харчову  продукцію на трьох підприємствах: на першому 40%  на другому 30% і на третьому 30%. Із цих замовлень неякісними можуть бути з першого – 1%, з другого – 1,5% і з третього – 2%. Яка ймовірність того, що навмання взятий товар виявиться неякісним.
18. (в) Імовірність влучення в ціль з першої гармати – 0,6, з другої – 0,9. Знайди ймовірність того, що при залпі по цілі влучать з обох гармат.
19. (д) Три стрільці виконали по одному пострілу. Імовірність влучення в ціль першим стрільцем – 0,8; другим – 0,75; а третім 0,7. Яка ймовірність хоча б одного влучення при одночасній стрільбі?
20. (в) Із 5 гвинтівок, серед яких 3 снайперські і дві звичайні, навмання вибирають одну і здійснюють постріл. Знайти ймовірність влучення, якщо ймовірність влучити зі снайперської гвинтівки дорівнює 0,95 а із звичайної – 0,7.
21. (д) Проводиться 10 незалежних пострілів по мішені. Імовірність влучення дорівнює 1/3. Знайди ймовірність того, що при такому випробуванні буде влучено не менше 8 разів.
22. (с) Кидають дві однакові монети. Яка Ймовірність того, що випадуть «герб» і «число»?
23. (д) Монету кидають 6 разів поспіль. Яка ймовірність того, що хоча б один раз випаде число?
24. (в) Монету кидають 5 разів поспіль. Яка ймовірність того, що «число» випаде не менше ніж 2 рази?

1. Що вивчає теорія ймовірностей?
2. Назвати основні поняття теорії ймовірностей.
3. Який дослід вважають стохастичним?
4. Що таке подія?
5. Що таке випробування?
6. Яку подію називають неможливою?
7. Яку подію називають вірогідною?
8. Яку подію називають випадковою?
9. Які події називають масовими?
10. Що таке повна група подій?
11. Які події називають сумісними в даному випробуванні?
12. Які події називають попарно несумісні?
13. Що таке рівноможливі події?
14. Що називають імовірністю випадкової події?
15. Чому дорівнює імовірність випадкової події?
16. Чому дорівнює імовірність неможливої події?
17. Яку умову задовольняє імовірність випадкової події?
18. Які події називаються протилежними?
19. Які події називаються залежними?
20. Які події називають складеними?