Подібність трикутників. Узагальнена теорема Фалеса

Мета уроку: навчати учнів змісту узагальненої теореми Фалеса, а також означення та властивості подібних трикутників; доповнити знання учнів історичними фактами з життя Фалеса та таких понять як пропорціональність відрізків та подібність фігур; формувати вміння застосовувати вивчені твердження під час розв’язування задач практичного змісту.

 Розвивати логічне мислення, пізнавальний інтерес, вміння використовувати власний досвід;

Виховувати товариськість, наполегливість, культуру спілкування.

Тип уроку:   урок засвоєння нових знань, умінь та навичок.

Обладнання: інтерактивний комплекс, ППЗ «Геометрія,8», презентація «Подібність трикутників», роздатковий матеріал (трикутники, кольорові картки).

Хід уроку.

I.  Організація класу.

Доброго дня! Я вас вітаю на уроці геометрії – уроці, що підтвердить слова: «Математика безмежно різноманітна і міститься в усьому».

Звернемо увагу на інтерактивну дошку.

    

 Які асоціації визивають у вас ці малюнки?(Відповіді учнів)

Мова на уроці йтиме про трикутники. Про які саме…Щоб знайти відповідь на це питання,  виконаємо практичне завдання: на парті у кожної групи лежить по три трикутники.

 Виключіть зайвий, на вашу думку. Поясніть свій вибір?

 Сумістіть однакові кути обох трикутників. Що ви можете тепер  сказати?

Висновок: Ці трикутники не рівні, але мають рівні кути, а сторони ні.

ІІ. Повідомлення теми, мети уроку.

 Ми з вами вивчаємо одну з найцікавіших тем геометрії «Означення подібних трикутників. Узагальнена теорема Фалеса.» Чому найцікавіших? Тому що знання узагальненої теореми Фалеса та означення подібності трикутників і їх властивостей допомагає в найнесподіваніші моменти. А деколи й рятує життя.

ІІІ.Робота з домашнім завданням:

Розділ ІІІ, §18, ст.116.    №2, №4, стор.118

На цьому етапі уроку, записавши до щоденника домашнє завдання, віднайдемо його в підручнику. Які нові поняття ви бачите в завданнях?

IV. Актуалізація опорних знань.

Давайте пригадаємо, що ми знаємо про трикутники.

Застосування методу гірлянд (гірлянди формуються як перелік основних понять, що повторювалися на уроці)

V.Вивчення нових знань.

Поглянемо на трикутники. На вашу думку, які трикутники називаються подібними?

(Можливі відповіді учнів, узагальнення їх. Висновок)

А тепер повернемось до електронного підручника:

1.                  Означення подібних трикутників.

(Запис означення )

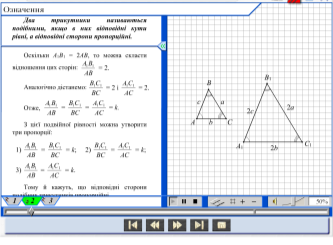
2.Алгоритм створення відношення відповідних сторін подібних трикутників.

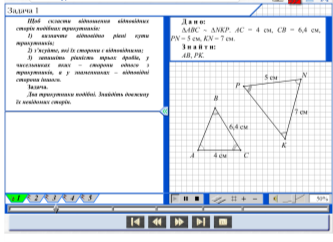
2.                    Поняття відношення і пропорції та учення про подібність фігур.

ФІзкультхвилинка

1. «Черепаха».

•                Голова плавно відкидається назад та дотикається потилицею спини – намагаємося втягнути голову в плечі. Потім плавний нахил голови вперед – знову тягнемо голову в себе.

2. «Сова».

•                Голова поставлена прямо, спина пряма. Повільно відводимо погляд вправо (вліво) та повертаємо за ним голову (намагаємося побачити, що там ззаду).

3. «Гарбуз».

•                Кругові рухи  голови. Шия – хвостик гарбуза, голова – гарбуз, перекачується  по плечах (без напруження).

Узагальнена теорема Фалеса.

Поняття відношення і пропорції виникло ще в далекій давнині.

3.                   

V. Формування вмінь, навичок учнів.

Групова робота

Утворимо групи: інформатиків, географів, біологів, архітекторів.

Завдання для інформатиків:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Завдання для географів:

Поняття подібності лежить в основі складання географічних карт, планів, креслення рисунків. На цьому понятті ґрунтується знімання місцевості.

 

Завдання для біологів:

Подібність предметів

Рівні фігури можна уявити як фігури, що мають однакову форму й однакові розміри. Але в повсякденному житті часто зустрічаються речі, які мають однакову форму, але різні розміри. У геометрії такі фігури називають подібними.

 

 

Завдання для архітекторів:

Пропорційність

Принципом подібності користувались ще художники і скульптори стародавнього Єгипту, коли їм треба було перевести рисунок на інше місце або збільшити його. У гробниці батька єгипетського фараона Рамзеса ІІ (ХІІІ ст. до н.е.) є стіна, вкрита сіткою квадратиків. За допомогою цієї сітки на стінку було перенесено в збільшеному вигляді рисунки менших розмірів.

 

VI. Застосування знань, формування вмінь.

 

Володіючи поняттям подібності трикутників, та знаючи узагальнену теорему Фалеса, можна визначати висоти предметів за їх тінню, знаходити висоту башти за її фотографією. Таким чином астрономи визначали висоти місцевих гір.

А чи зможемо й ми скористатися знаннями з геометрії за необхідності? Давайте спробуємо. Для цього об’єднаємося в 3 групи: архітекторів, географів, лікарів.

 

 

 

 

Завдання

Розв’язання.

Треба виміряти довжину сторони основи і висоту самої вежі на фотографії, а потім довжину сторони основи самої вежі. Виконавши всі обчислення маємо, що висота вежі дорівнює 317м, не враховуючи висоту антени, а з нею 322м.

 

Завдання

 

 

 

Розв’язання.

1)Приведемо всі одиниці вимірювання до (м):

12740км=12740000м

3мм= 0,003м

2)Враховуючи, що глобус пропорційний об’єкт  до земної кулі, г.Говерла буде пропорційна своєму зображенню, складемо відношення:

 

Завдання

 

Беручи за величину букви на класній дошці А₁В₁=х, з подібності трикутників ОВА і ОВ₁А₁, матимемо:

х=2,1(см)  Відповідь: 2,1см

 

Учні пояснюють розв’язання задач, записують розв’язки в зошити.

VII. Підсумки уроку.

VI. Домашнє завдання. Розділ ІІІ, §18, ст.116