МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Відокремлений структурний підрозділ 

«Мелітопольський фаховий коледж Таврійського державного агротехнологічного університету  імені Дмитра Моторного»

        

Циклова комісія загальноосвітньої підготовки

 

 

 

 

Лекція  з теми

«Похідна функції.  Диференціювання алгебраїчних  та тригонометричних функцій»

 

З ДИСЦИПЛІНИ «Вища математика»

Мелітополь, 2021

 

 

 

 

Тема: Похідна функції. Диференціювання алгебраїчних та тригонометричних функцій.

            Мета:           1. Вивчити основні визначення.

2.              Знати правила диференціювання.

3.              Вміти застосовувати правило диференціювання, формули диференціювання алгебраїчних, тригонометричних функцій. 

Час. 2 год.

Література:  [4], гл. 3, [5], гл. 7. 

1. Теоретичні відомості.

      Означення. Похідною y _ ^dy від функції y  f (x)у точці x по dx

аргументу xназивається границя відношення ^y ,коли x прямує до нуля, x

отже y  dy  lim ^y ,якщо ця границя існує.

                          dx     x0 x

Основні правила знаходження похідної.

Якщо С – стала і u  u(x),v  v(x),w  w(x) функції, що мають похідну, то:

1.(C)  0

2.(x) 1

3.(u  v)  u  v

4.(C u)  C u

5.(u v)  uv  uv                                                                u     uv 2uv,                                  6.                                          v           v 7.C    Cv2,                                      v          v

(v  0) (v  0)

8.(u vw)  uvw  u vw  u vw. Таблиця похідних основних функцій.

1.(uⁿ)  nu^n1 u

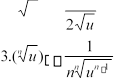1

2.( n)          u

u

4.(a^u )  a^u ln a u

5.(e^u)  e^u u

1

6.(log_a u)   u u ln a

1

7.(lnu)     u u

8.(sinu)  cosu u

9.(cosu)  sinu u

1

10.(tgu)  cos₂ u u

1

11.(ctg u)   sin₂ u u

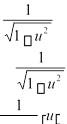12.(arcsin u)            u  

13.(arccosu)              u

14.(arctg u)  1 u₂

1

15.(arcctg u)  1 u₂ u

                                           16.(u^v )  u^v lnuv vu^v1 u.

 

Правило диференціювання складеної функції.

Якщо y  f (u) і u (x),от же y  f[(x)],де функції y іu мають похідні, то

                                            dy       dy du

y_x  y_u u_x ,або              .

                                            dx      du dx

Це правило розповсюджується на ланцюг з будь-якого кінцевого числа             диференціалів.   

Логарифмічне диференціювання. 

Якщо треба продиференціювати добуток кількох функцій або дріб, чисельник і знаменник якого містить добутки, часто буває зручніше обидві частини даного виразу спочатку прологарифмувати по основі e, а потім вже приступити до диференціювання. 

Цим прийомом краще користуватись при диференціюванні степеневопоказникових функцій, тобто функцій виду y U ^v , де U U(x),v  v(x),або у випадку відношення та добутку кількох функцій більш ніж двох.   

                                              Диференціювання неявних функцій.                

Якщо незалежна змінна xі функція y зв’язані рівнянням f (x, y)  0,яке не розв’язане відносно y,то y називається неявною функцією. 

Правило диференціювання таких функцій полягає в тому, що обидві частини рівняння f (x, y)  0 диференціюються по x з урахуванням, що y є функція xта потім з отриманого рівняння визначається y.

                                  Диференціювання функцій, заданий параметрично. 

В геометрії та механіці часто вживається так названий параметричний спосіб надання рівняння кривої. Крива в цьому випадку визначається двома рівняннями:

x  ^{(t) }_,     tt₁;t₂                                    (9.1)

y  (t)_

де t допоміжна змінна, що називається параметром.

Якщо з рівняння (9.1) можна виключити параметр t,то y визначається як явна або неявна функція x.Але виключення параметра t із рівнянь виду (9.1) є в більшості випадків неможливо. Тому користуються формулою:

                                                                       y_x  ^yt                                                (9.2) x_t

                                              Геометричний зміст похідної. 

Похідна від функції f (x), що вираховується при заданому значенні x, дорівнює тангенсу кута, який створюється додатнім напрямком осі Oxі додатнім напрямком дотичної (тобто напрямком дотичної, в якому збільшується абсциса), проведеної до графіка цієї функції в точці з абсцисою x.

Для визначення рівняння дотичної до графіка функції в точці (x₀, y₀) користуються наступною формулою:

                                                     y  y(x₀)(x  x₀)  y₀                                   (9.3)

                                              Механічне значення похідної.

Закон матеріальної точки, що рухається, вважається заданим, якщо її шлях S є відомою функцією часу t,тобто якщо 

                                                     S _ f (t)                                                      (9.4)

(Sвідстань точки що рухається від початку відліку).

Швидкістю руху в даний момент часу t₀ є значення першої похідної від шляху при t  t₀ :

                                              v  S(t₀)  f (t₀)                                              (9.5)

 

2. Практична частина.

Диференціювання алгебраїчних функцій.

Приклад 1. Знайти похідну функції: 1) y  x⁵,   2) y  x,    3) y  ⁴ x³ Розв’язок.  Використовуємо формулу (1) таблиці, те що (x) 1.

1)    В цьому прикладі показник степеня n  5,тому y  5x⁴.

1

2)    Тут n _ ¹ , тому y  ( x)  (x )  ¹ x^21  ¹ x^   . 

                                                                         22                                    2            2 x

При рішенні цього прикладу можна було використати формулу (2).

3

3)    Тут n _ ³, тому y  (⁴ x³ )  (x )  ³ x^41  ³ x^  .

                                                                          44                                     4

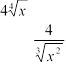             Приклад 2. Знайти похідну функцій 1) y  5x³, 2) y           .

Розв’язок. Враховуємо правило знаходження похідної №4 та формулу таблиці (1).

1)  Тут n3 y  (5x³)  5(x³)  53x² 15x²;

2)  Тут n2/3

                                                                              2 5

y   3 4x2   4x^3   4^ 2^ x^{ 1}  8 x ³     8          ,

                                                                              3               3            3₃ x₅

В прикладі 2) можна було використати правло знаходження похідної №7.

Приклад 3. Знайти похідну функції     y  27x3  81x23 x2  6 11.

                                                                                          2                  3 x

Розв’язок. Надана функція є алгебраїчна сума декількох функцій, тому використаємо правило №3 наряду з (1); насамперед переходячи до дрібних показників степенів:

y  27x3  81x83  6x 11  27(x3)  81x82   6x13   (11)  273x31  81 8  x831 

                       2                                          2                                            2    3



 6^_ ^1_x^1 0  81x² 108 x  2x^ 81x² 108x x         .

          3

Приклад 4. Знайти похідну функції y  (5x²  7x  2)³.

Розв’язок. Тут ми маємо справу зі складною функцією. Нехай u  5x²  7x  2, тоді y  3u² u  3(5x²  7x  2)² (5x²  7x  2)  3(5x²  7x  2)²(10x  7).

Але можна і не використовувати проміжні записи, тобто введення змінної u.

                                                                                                   ^                 3^4

             Приклад 5. Знайти похідну   y  1 2 x      .

                                                                                                                   x 

Розв’язок.

                                            4                               3                                                                             3

              1 2 x     

y  _^ 3x  ^_  41 2 x  3x  1 2 x  3x   41 2 x  3x  2 21x 3 x12  

3

 4^1 2 x  3x ^ _^1x  x3₂ ^_.

Приклад 6. Знайти похідну функції y  (3x² 5ax  2a²) a² 3x² .

Розв’язок. Тут треба продиференціювати добуток двох функцій використовуючи правило №5. 

y  (3x² 5ax  2a²) a² 3x²  (3x² 5ax  2a²)( a² 3x² ) 

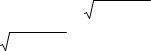
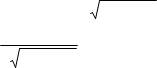
                                            ²          3x²  (3x² 5ax  2a²)          1            6x  (6x 5a) a² 3x² 

 (6x 5a) a 

2 a² 3x²

                        ²        5ax  2a²)       3x       . 

 (3x  a² 3x²

5 3x  x²

Приклад 7. Знайти похідну y  53x  x₂ .

Розв’язок. Тут слід використати правило №6 – диференціювання дробу.

y_{ } (53x  x²)(53x(5x²)  (52)32x  x²)(53x  x²) _

_3x _ x

(3 2x)(53x  x²)  (5 3x  x²)(3 2x)

 ,

        а після спрощень     .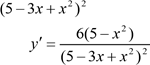

Диференціювання тригонометричних функцій. Приклад 8. Знайти похідну

1)y  sin15x, 2)y  cos2x² 3)y  tg 1^{ x}; 4)y  ctg  ¹          .

                                                                                      x                        1 x

Розв’язок. 

Використовуємо формули (8), (9), (10), (11) і правило диференціювання складеної функції.

1)         y  (sin15x)  cos15x(15x)  cos15x15 15cos15x;

 

2)         y  (cos2x²)  sin2x²(2x²)  sin2x² 4x  4xsin2x²;

3)         y_{ } _tg 1 x ^ _         1          _ 1 x ^ _      1          _ (1 x)x  (1 x)(x) _

=

1)    Задачу перепишемо у вигляді:          y  arcsinU, U  2x.Тоді по формулі диференціювання (12)              y _     ¹          _U _ ¹          _(2x) _         ¹ _2 _    ²          .

                                              1U²                              1 4x²                                      1(2x)²                           1 4x²

В подальшому будемо обходитися без введення проміжного аргументу. 

2)    y  (arccos x^m )     ¹          (x^m )          ¹          m x^m1.

                                                             1(x^m )²                                          1 x^2m

Тут використали        формулу     диференціювання          (13)   і         правилом диференціювання складених функцій. 

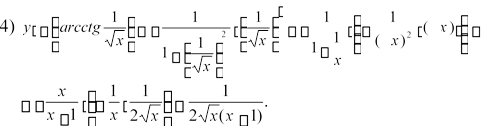
3)    y  (arctg x) ^ 1 (¹ x)₂ ( x)  1_¹x  2¹x  2 x(¹1_ x). Були використані формула (14) і правило диференціювання складеної функції.

Користувалися формулою (15) і правилом диференціювання складеної функції.

Приклад 10. Знайти похідну

1)y  ln(ax  b),    4)y  ln arctgx,           _{7)y  ln(ln x),}

2)y  ln⁵ x,   5)y  ^{ln x} ,    x  _a

8)y  ln.

3)y  lnsin x,x  a

6)y  ln(x 

Розв’язок. 

1)    y  (ln(ax b))            ¹            (ax b)    ¹          a     ^a          ;

                                                              ax b                     ax b          ax b

2)    y  (ln⁵ x)  5ln⁴ x(ln x)  5ln⁴ x ¹; x

3)    y  (lnsin x)     ¹  (sin x)      ¹  cos x  ctgx;

                                                       sin x                  sin x

4)    y  (lnarctgx)   (arctgx)  ;

1

5)    y_{ } _ ln x _^ _ (ln x)x 2ln x(x) _ x ^{ x }x2^{ln x1} _ 1xln2 x ;



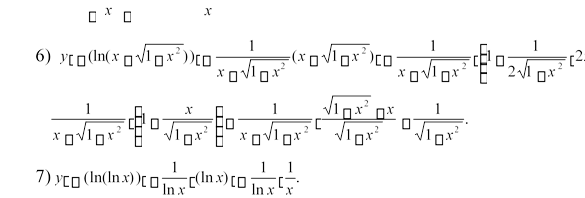
8) Спочатку за властивостями логарифмів перетворимо функцію:

y  ln    x ^{ a} _ ¹ ln^_ ^{x  a }_  ¹ (ln(x  a)  ln(x  a)) x  a       2           x  a         2

y   1 (ln(x  a)  ln(x  a)  1  1                       1    x  a  (x  a) 

                       2                                      2 x  a   x  a    2(x  a)(x  a)

                          2a                a

 2(x2 a2)  x2 _ a2 .

Приклад 11. Знайти похідну функцій

⁴ x²  7x 8 ⁶ x⁴ 1

1)y ;

                                      ³ e^x ctg ²x           

2)y  (sin x)^cosx.

Розв’язок. 

1) Прологарифмуємо ліву та праву частини функції по основі e і пристосуємо властивості логарифмів, визначивши праву частину:

ln y  ln ⁴ x²  7x 8 ⁶ x⁴ 1;

³ e^x ctg²x

ln y  ln(x²  7x 8)  ln(x⁴ 1)   x  2lnctgx

Продиференціюємо ліву та праву частини отриманого рівняння з урахуванням, що y - функція від x.

         ¹y  y  ¹4 x^{2 1}7x 7 (x²  7x 8)  ¹ x4¹ 1(x⁴ 1)  ¹3  2 ctgx¹         (ctgx);

                                         _{      }                               6      _

             1               2x  7               2x³                  1             2

y y^{ } 4(x²  7x 8) ^ 3(x⁴ 1) ^ 3 ^ ctgx sin² x ; 

помножуємо ліву та праву частини рівняння на y,отримуємо:

                               2x  7              2x³                          4        1

y^{ } y^ 4(x²  7x 8 ^ 3(x⁴ 1) ^ sin2x ^ 3^_;

внаслідок маємо:

                          ⁴ x²  7x 8 ⁶ x⁴ 1         2x  7               2x³                        4       1

            y           ³ e^x ctg²x      4(x2  7x 8)  3(x4 1)  sin x  3.

2) Надана функція також потребує застосовування логарифмічного диференціювання, тобто використовуємо той же метод. 

ln y  ln(sin x)^cosx , ln y  cos xlnsin x,

1  y  (cos x)lnsin x  cos x(lnsin x),

y

             1                                               1

y y  sin xlnsin x  cos x sin x cos x,

                                                     cos² x 

y  y_sin xlnsin x  sin x _,

^{cosx } cos² x sin xlnsin x_. y  (sin x) _ sin x  _

_

 Ця функція носить назву степенево-показникової, і її похідну можна знайти використовуючи формулу таблиці похідних (16). 

y  ((sin x)^cosx )  (sin x)^cosx lnsin x(cos x) cos x(sin x)^cosx1 (sin x) 

         (sin x)^cosx lnsin x(sin x)  cos x (sinsinx)xcosx                         sin   cosx_^ sin xlnsin x  cos2 x ^.

                                                                                                          cos x  (     x)                           sin x 

Приклад 12. Знайти похідну від неявної функції 5xy² 3y 7  0.

Розв’язок. Диференціюємо по x обидві частини рівняння і враховуючи, що   y є функція от x;  похідна правої частини рівняння дорівнює нулю, отримуємо: 

                                   ² 5 x2y y3y  0, y(10xy 3)  5y², y   5y²          .

                  5y 

10xy 3 Приклад 13. Найти похідну y неявних функцій:

                                    1)x²  y²  25  0; 2)x³  y³ 3axy  0.

Розв’язок.

Диференціюємо з урахуванням того, що y функція x і виражаємо y.

1)      2x  2y  y  0

2y  y  2x;

                     y _{ } ^2x ;  

2y x y    .

y

2)      3x² 3y²  y3a(y  x y)  0

 

3x² 3y² y3ay 3axy  0 виражаємо y.

y(3y² 3ax)  3ay 3x²;

3ay 3x²         y  3y2 3ax ;

Скорочуємо на 3:

y  ayy2 xax2 .

Приклад 14. Знайти похідну: ln xy  xy²  0. Розв’язок. 

            ¹ (y  x y)  (y²  x2y  y)  0,

x y

Помножимо обидві частини рівняння на xy :

y  x y  xy³  2x² y² y  0; y(x  2x² y²)  xy³  y; xy³  y y  x  2 y2 .

2x

Приклад 15. Знайти похідну y_x від функцій, заданих параметрично:

x  asint

            1)_                 (0  t  2);

_y  bcost

2)^x _ 1absincost t ;

_y _ ccost

                    1 bcost                

                ^x  arcsin      ^t      ;           x  y  ^

_^₂

                                  3)                               _

                 y  arccos             .             y   x     y_x  1.

_2

Розв’язок. 

Знаходимо x_t і y_t і отримані значення підставляємо в (9.2):

1)     x_t  acost; y_t  bsint

y_x _ y_t _ bsint _{ } b tgt. x_t     acost    a

2)xt_{ } a cost(1b(1cosbt)cos(t)b2sint)sint _ a cost (1b_cosbcos² t t)b2 sin² t _ (a1(_cosbcost tb))2 ;

yt _ c sint(1b(1cos t) (2bsint)cost _{ } (1_cbsincostt)2 ;

bcost)

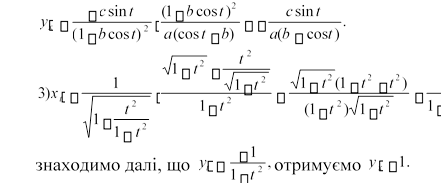
Приклад 16. Знайти похідну y_x від функції, заданої параметрично:

x    2cost  cost  y  2sint sin2t^_ 

у точці, де t  ^. 6

Розв’язок. 

                                                                           3t       t

            x_t  2sint  2sin2t  4cos    sin    ;

                                                                            2       2

                                                                         3t       t

             y_t  2cost  2cos2t  4sin    sin    ,

                                                                          2       2

         а тому y_x  tg 3t , y_x^_^_^ tg ^3  tg^ 1.

                                                 2            6        2 6          4

Приклад 17. Написати рівняння дотичної y  (x 1)³ 3 x в точках a) A(1;0),б)B(2;3).

Розв’язок. 

Знайдемо похідну функції та скористуємося формулою (9.3).

y  ³ 3 x  (x 1) ^1 .Визначимо значення похідної при x1 3³ (3 x)²

            а) y(1)  ³ 3(1)  (11)      ^1             4

Підставляємо в (9.3): y  ³ 4(x (1))  0  або  y 

б) y(2)  ³ 3 2  (2 1)

y    0(x 2) 3  або  y  3.

Приклад 18. Заданий закон S(t)руху матеріальної точки. Треба знайти значення скорості та прискорення цієї точки в момент часу t₀.

                                                S(t)  3x⁴  2x³  x 1, t₀  2.

Розв’язок. 

Відомо, що значення швидкості та прискорення матеріальної точки в якійсь момент часу є відповідно значення в цей момент першої і другої похідних функції, що задає закон руху точки. 

У нас S(t) 12x³ 6x² 1, v(2)  S(2)  73(од.ск.)  S(t)  36x² 12x, a(2)  S(2) 120(од.приск.) Самостійна робота.

1. Найти похідні.

1)    e^x  x  y³  0

2)    xln x 32y  0

2. Знайти y_x

              1)   x  t 2tgt3,t3,              12))arctgxtgx  4lnx  52y230 0

y  3t 

2)     _xy  arcsin3t t3t,,    1)xy  aa((sincosttttcossintt)),,         2)xy  ctgtsec2,t,

3.  Під яким кутом крива y  ln xперетне ось Ox?

4.  Заданий закон S(t)  4x⁴  2x³ 7x² 3 зміни шляху матеріальної точки.

Знайти значення скорості та прискорення цієї точки в момент часу t₀ 1.

5.  Написати рівняння дотичної xy ln y 1в точці M(1;1).

         Домашня робота. 

Знайти похідні функцій:

                2                       ²         x;

1)y           7x x  3x 

x

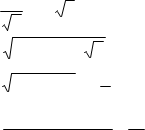
32))yy                    8x²  4x  ³ x;  3 arccos x;        2)y     ₁ 2x ; x 1)y 

               3 2x2 10x tg     ;                                                                                     arctg

4)  y  5 5 x ⁴  5 ctg ^arcctg7x log₂ x; 4)y  arcsin 5x2 ; 3cosecx  2sin x 16 _52x;             3)y  8  _{1 25x}

cos

5)  y        24 x  cos32 x sin x.       5)y  (x3  x2)ex 1;   6)y  (x  ex )x7.

cos

                                               1)y  arcsin³ x²;   2)y  arctg³ x³₃ ; 3)y  arccos⁴ 5x

                                              4) y  arcctg   ln x; 5)y  arctg a ^{ x} ;

1 ax

6)  y  lnarcsin7)y  5^ctg2x arccos8x. 

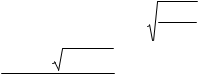8)y  ln(15e^x  x²); 9)y  ln 9 1^x 4 ; x

                                              10)y  (x  52)²⁵ (x  4)³                                        tgx.

                                                                                                     ;   11)y _ x

2^{x 1}(x  4) Питання для самоперевірки:

1.     Що ми називаємо похідною?

2.     Основні правила диференціювання.

3.     Диференціювання складеної функції.

4.     Диференціювання степеневої функції.

5.     Диференціювання тригонометричних функцій.

6.     Основні правила диференціювання.

7.     Для яких функцій використовують логарифмічне диференціювання?

8.     Основні етапи логарифмічного диференціювання. 

9.     Дати означення функції заданою неявно. 

10.Правило знаходження похідної неявно заданої функції.

11.Параметрично задана функція та її диференціювання.

12.Геометричний зміст похідної.

13.Механічний зміст похідної.