МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Відокремлений структурний підрозділ 

«Мелітопольський фаховий коледж Таврійського державного агротехнологічного університету  імені Дмитра Моторного»

        

Циклова комісія загальноосвітньої підготовки

 

 

 

 

Лекція  з теми

«Застосування диференціального числення для дослідження функцій  і побудови їх графіків»

 

З ДИСЦИПЛІНИ «Вища математика»

                                              

УКЛАДАЧ: БОЙКО СВІТЛАНА БОРИСІВНА, 

 ВИКЛАДАЧ МАТЕМАТИЧНИХ ДИСЦИПЛІН

 

Мелітополь, 2021

 

 

 

 

 

Тема: Застосування диференціального числення для дослідження функцій  і побудови їх графіків.

Мета: 1. Вивчити основні визначення.

2.                      Знати правила застосування диференціювання.

3.                      Вміти          застосовувати      похідну       для    дослідження         функцій             і побудови їх графіків. Час. 2 год.

             Література:  [4], гл. 4,     [5], гл. 8. 

1. Теоретичні відомості.

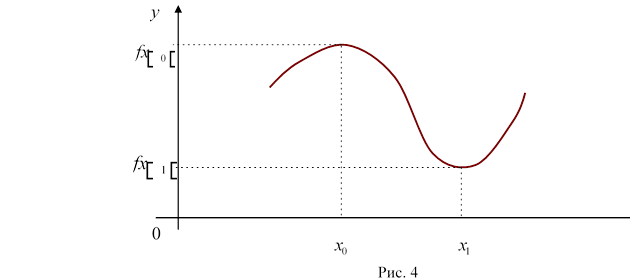
Означення 1. Точка x₀ називається точкою максимуму функції y  f x , якщо f x ₀  f x  для всіх x  x₀ з деякого околу точки x₀ . 

Означення 2. Точка x₁ називається точкою мінімуму функції y  f x , якщо f x ₁  f x  для всіх x x ₁ з деякого околу точки x₁.

Означення 3. Значення функції в точці максимуму f x₀ називається максимумом функції, а значення функції в точці  мінімуму f x₁ – мінімумом функції .Спільна назва максимумів і мінімумів функції – екстремуми (рис. 4).

 

Необхідна умова екстремуму

Якщо функція y  f x  має екстремум в точці x  x₀, то f x₀  0 або f x₀ не існує.

Точки, в яких похідна функції y  f x  дорівнює нулю або не існує називаються критичними точками.

Для того, щоб визначити чи існує екстремум у критичній точці, треба застосувати достатні умови екстремуму.

Достатні умови екстремуму

Перша достатня умова екстремуму

Нехай x₀ – критична точка функції y  f x . Якщо при переході через критичну точку зліва направо похідна функції f x змінює знак з мінуса на плюс, то x₀ – точка мінімуму.

Якщо при переході через критичну точку зліва направо похідна функції змінює знак з плюса на мінус, то x₀ – точка максимуму.

Правило дослідження функції на екстремум Для того, щоб дослідити функцію на екстремум треба:

1.       Знайти область визначення функції.

2.       Знайти похідну і критичні точки функції.

3.       Знайти знак похідної зліва та справа від кожної критичної точки.

4.       Визначити характер кожної критичної точки, обчислити екстремуми функції.

Друга достатня ознака екстремуму

Нехай функція y  f x  двічі диференційована в деякому околі точки x₀ .

Тоді: якщо f ^x₀  0,то x₀ – точка мінімуму; якщо f x₀  0,то x₀ точка максимуму;

 

Правило дослідження функції на екстремум Для того, щоб дослідити функцію на екстремум потрібно:

1.     Знайти область визначення функції.

2.     Знайти похідну функції і критичні точки функції, розв’язуючи рівняння f x  0.

3.     Знайти другу похідну і обчислити її значення в критичних точках. 

4.     Визначити характер кожної критичної точки, обчислити екстремуми функції.

Слід мати на увазі, що найбільше і найменше значення на відрізку a b;  неперервна функція може досягати або в точках екстремуму, що належать відрізку, або на кінцях цього відрізка.

Але якщо функція має єдиний максимум (мінімум) на відрізку a b; , то вона досягає найбільшого (найменшого) значення саме в точці максимуму (мінімуму).

Розв’язання задачі на знаходження найбільшого або найменшого значення передбачає:

1.     Складання функції, найбільше або найменше значення якої потрібно знайти;

2.     Знаходження області визначення цієї функції згідно з її фізичним або геометричним змістом.

3.     Дослідження на екстремум цієї функції. Для того, щоб дослідити функцію та побудувати її графік, треба:

1.     Знайти область існування функції.

2.     Дослідити функцію на неперервність, знайти характер точок розриву.

3.     Дослідити функцію на парність.

4.     Якщо функція періодична, то знайти її період.

5.     Знайти першу похідну функції, інтервали зростання та спадання, екстремуми функції.

6.     Знайти другу похідну функції, інтервали опуклості та угнутості, точки перегину.

7.     Знайти асимптоти графіка функції.

8.     Якщо це можливо, знайти точки перетину графіка функції з осями координат, інтервали знакосталості функції.

9.     Побудувати графік.

2. Практична частина

Приклад 1. Потрібно виготовити закритий зверху циліндричний бак максимального об’єму. Якими повинні бути радіус основи і висоти циліндра, якщо на його виготовлення є S  6 (м²) матеріалу?

Розв’язання. 

                                       r                                               Нехай x – радіус основи,

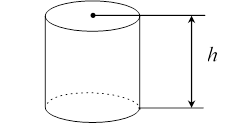h – висота циліндра Тоді V x h² .

                                                                                 ²        2 xh, звідси h  S  2x²

Повна поверхня S  2 x 

2x

Об’єм виразимо як функцію від x:

 

                                                 V x² S 22xx2  12        3 ,        x  0 .

Sx  2x 

Дослідимо цю функцію на максимум.

V x( )  S  6x²;  V x( ) 0 ,  знаходимо критичну точку S  6x²  0; x _ ^S . Якщо S 6, то x_кр 1.

6

Знайдемо другу похідну V( )x  (12x)  6x; V(1)  6 0, що означає, що при x 1 функція V x  має максимум.

При цьому h _ 6^{ } 2      _ 2. 

2

Отже, V V_max , якщо радіус основи 1 м, а висота 2 м.

x²  3

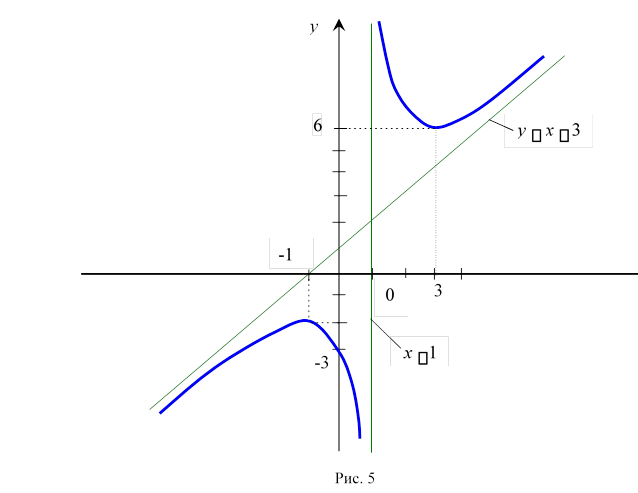
Приклад 2. Дослідити та побудувати графік для функції y   . x 1

Розв’язання.

        1.Область існування D f    ;11;

                                       x2 ^{ 3                     x2  3}

2.     lim   ;  lim   ;  x 1 – це точка розриву другого x1 0 x 1 x1 0 x 1 роду, а пряма x 1 – вертикальна асимптота.

3.     Вісь Ox графік функції не перетинає, оскільки x²  3  0. Графік функції перетинає вісь Oy у точці y  3.

На проміжку ;1 y  0, при x1; y  0 x²  3

4.     Оскільки f (x)    f x( ) , f (x)   f x( ), то функція ані парна, ані  x 1

непарна.

5.     Функція неперіодична.

6.     Визначимо похилі асимптоти:

3

k  lim f x( )  lim x^{2  3} _ lim1 ^x2 _1 x x      x x x 1      x 1_ 1

x

                                                                                                             x² 3               x3

b  lim( ( ) f x kx)  lim x1  x lim_x x1 1 _{x x}



 

y  x 1 – похила асимптота

7.     Знайдемо екстремуми та проміжки зростання та спадання функції:

 ²       3   2 (x x 1)  x²  3 x²  2x  3 x 

                                                    y'   x 1      x 12           x 12    



                  При y'  0  x²  2x  3  0, x₁ 1,      x₂ 3.

У інтервалі ;1  y'  0  функція зростає,

у інтервалі 1;1   y'  0  функція спадає, у інтервалі 1;3     y'  0  функція спадає,

у інтервалі 3;    y'  0  функція зростає.

Оскільки при переході через критичну точку x₁  1 похідна змінює знак з плюса на мінус, то точка x₁  1 – точка max:

y_max(1)  2

Оскільки при переході через критичну точку x₂ 3 похідна змінює знак з мінуса на плюс, то точка x₂ 3 – точка min: y_min (3) 6.

 

8.Знайдемо інтервали опуклості, вгнутості та точки перегину.

                                                          (2x  2)(x 1)²  2(x 1)(x²  2x  3)        8

                                                y"                                 ₄                                                 ₃

                                                                                              x 1                 x 1

Оскільки y" не може бути рівною нулю, точок перегину немає, в інтервалі ;1 y"  0 і крива опукла, в інтервалі 1; y"  0 , крива вгнута.

9.Будуємо графік (рис.5).

 

Самостійна робота.

Побудувати графiки функцiй за допомогою першої або другої похiдної:

y  2x³ 3x² 5

y  x²(x2)² y e^x e^x

         Домашня робота. 

Побудувати графiки функцiй за допомогою першої або другої похiдної:

y  2x³ 3x² 12x8 y3³ x² x

Питання для самоперевірки:

1.          Означення зростаючої та спадної функцій. Необхідні і достатні ознаки зростання (спадання) функції (сформулювати).

2.          Означення екстремуму функції однієї змінної. Теорема Ферма. Необхідна ознака існування екстремуму. Критичні точки функції.

3.          Дослідження функцій на екстремум за допомогою першої похідної. Перша достатня ознака існування екстремуму. Робоче правило.

4.          Дослідження функцій на екстремум за допомогою другої похідної. Друга достатня ознака існування екстремуму. Робоче правило.

5.          Найбільше і найменше значення функції на відрізку. 

6.          Означення опуклості та вгнутості кривої. Достатня умова опуклості (вгнутості) графіка функції. Точки перегину. Достатня умова існування точок перегину (сформулювати).

7.          Поняття про асимптоти графіка функції. Знаходження вертикальних, похилих, горизонтальних асимптот.

8.          Загальна схема дослідження функції та побудови графіка.