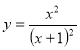Похідна функції та її застосування

ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ САМОСТІЙНОЇ РОБОТИ

Тема. Похідна функції та її застосування

Мета: Виробити практичні навички обчислення похідної; застосовувати похідну до обчислення наближених значень; проводити дослідження та будувати графік функції.             

Контрольні запитання:

1. Означення похідної функції в точці.
2. Геометричний зміст похідної функції в точці.
3. Фізичний зміст першої похідної.
4. Що таке диференціювання?
5. Яка функція називається диференційованою?
6. Чому рівна похідна суми функцій?
7. Чому рівна похідна добутку двох функцій?
8. Чому рівна похідна добутку сталого числа на функцію?
9. Чому рівна похідна частки функцій?
10. Означення другої похідної.
11. Фізичний зміст другої похідної.
12. Чому рівний кутовий коефіцієнт дотичної до графіка функції в точці?
13. Записати загальне рівняння дотичної.

Методичні вказівки до розв’язування завдань самостійної роботи.

Приклад 1. Обчислити похідну функції

Розв’язування: Скористаємось правилом обчислення похідної від добутку: .

Приклад 2. Обчислити похідну функції

Розв’язування: Скористаємось правилом обчислення похідної від частки: .

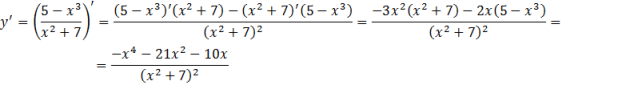
Приклад 3. Обчислити похідну складеної функції: .

Розв’язування: Спочатку перетворимо функцію, використовуючи властивості логарифмів: .

Диференціюючи, отримаємо:

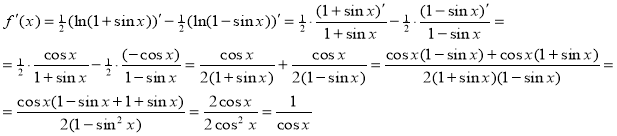
Приклад 4. Обчислити наближене значення функції в даній точці .

Розв’язування: Скористаємось формулою наближених обчислень за допомогою диференціала:

Для цього обчислимо додатково ; :

За беремо число близьке до даного, але для якого значення виразу обчислити легше. В даному випадку . Обчислимо . Знайдемо значення функції в точці :

Обчислимо похідну функції і обчислимо її значення при .

Підставимо отримані результати в формулу:

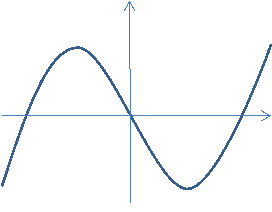
Приклад 5. Побудувати графік функції: у=х³-3х.

1. Областю визначення є множина всіх дійсних чисел, тобто х=R.
2. Дослідимо функцію на парність: 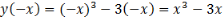. Функція непарна, отже графік симетричний відносно початку координат.
3. Знайдемо точки перетину графіка функції з осями координат:

З віссю Ох:        

 З віссю Оу:

4.    Знаходимо екстремуми функції. Для цього спочатку знайдемо похідну 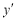=3х²-3. Потім знаходимо критичні точки: 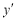=0, 3х²-3=0, х₁=1, х₂=-1. Відмітимо ці точки на числовій прямій (мал.1). Дослідимо знак похідної на кожному інтервалі: 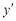(-2)>0, 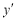(0)<0, 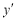(2)>0. Функція зростає при 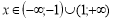і спадає при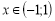. Отже, х=-1 – точка максимуму; у_max=у(-1)=(-1)³-3(-1)=-1+3=2; х=1 – точка мінімуму; у_min=у(1)=1³-3∙1=1-3=-2.

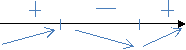 Позначимо всі отримані точки в системі координат і сполучимо їх плавною кривою (мал.2).

     -1     1

(мал.1)

y

2

  -1 0       1           x

-2

(мал.2).

Література:

1. Бевз Г.П., Бевз В.Г Математика 10.Рівень стандарту. – К.: Генеза, 2011 р.

 §6-12 стор.502-86.

2. Афанасьєва О.М., Бродський Я.С. Математика. – К.: Вища школа, 2001 р.

 §1,2 стор.112-151. 

3. М.І.Шкіль Алгебра і початки аналізу 10-11 кл. – Київ “Зодіак-ЕКО”, 2002 р.

Розділ 7, §2-3 стор.295,299, Розділ 8, §5 стор.335. 

Критерії оцінювання:

Робота містить 5 завдань: №№1-4 по 2 бали, №5 по 3 бали

Бали за виконання завдань №№1-4 відповідно виставляються :

  а) за правильну відповідь і записи без помилок  (2 бали);

б) за правильну відповідь і записи з помилками або за неправильну відповідь і відповідні записи, які свідчать про самостійність розв’язування  (1 бал);

в) у решті випадків 0 балів.

Бали за виконання завдання №5 відповідно виставляються :

  а) за правильну відповідь, записи без помилок і правильно виконаний рисунок (3 бали);

б) за правильну відповідь і записи з помилками чи неточність при побудові (2 бала);

в) за неправильну відповідь і відповідні записи, які свідчать про самостійність розв’язування  (1 бал);

г) у решті випадків 0 балів.

Завдання для самостійного виконання:

1. знайти похідну добутку функцій;
2. знайти похідну частки функцій;
3. знайти похідну складеної функції;
4. обчислити наближене значення функції 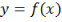в даній точці;
5. провести дослідження і побудувати графік функції.