Рівняння та нерівності для підготовки до ЗНО
РІВНЯННЯ ТА НЕРІВНОСТІ ПІДГОТОВКА ДО ДПА З МАТЕМАТИКИ
Варіант 1
Частина перша
1.1. Чому дорівнює корінь рівняння ![]() ?
?
А) 2; Б) 3; В) 6; Г) 9.
1.2. Знайти корінь рівняння 9x = 27.
А) 3; Б) 1,5; В) 2; Г) 0,5.
1.3. Розв’язати нерівність ![]() .
.
А) (6;∞); Б) (-∞;6); В) (0;6); Г) (0;6)ᴗ(6;∞).
1.4. Розв’язати нерівність  .
.
А)![]() ; Б) (0;∞); В) (∞;1); Г) (∞;0).
; Б) (0;∞); В) (∞;1); Г) (∞;0).
1.5. Коренем якого рівняння є число 16?
А) log8 x=2; Б) log2 x=8; В) log4 x=2; Г) log4 x=4.
Частина друга
2.1. Установити відповідність між рівняннями (1–4) і сумами їх розв’язків (А–Д):
1. ![]() А –3
А –3
2. ![]() Б –8
Б –8
3. ![]() В –16
В –16
4. ![]() Г –7
Г –7
Д –12
Частина третя
3.1. Розв’язати рівняння: ![]() .
.
3.2. Розв’язати нерівність log 9 (4 3х) < 0,5.
Варіант 2
Частина перша
1.1. Розв’язати рівняння х3=9.
А) 3; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() ;
;![]() .
.
1.2. Розв’язати рівняння ![]() .
.
А) 1; Б) 1; В) 0; Г) коренів немає.
1.3. Розв’язати нерівність ![]() .
.
А) (-∞;3] ; Б) (0;3] ; В) [0;3] ; Г) (-∞;9].
1.4. Розв’язати нерівність ![]() .
.
А) (∞;3]; Б) [3; ∞); В) (∞;3]; Г) [3; ∞).
1.5. Знайти суму коренів рівняння ![]() .
.
А) 9; Б) 7 ; В) 1; Г) 1.
Частина друга
2.1. Установити відповідність між нерівностями (1–4) та множинами їх розв’язків (А–Д):
1. ![]() А [–2;4]
А [–2;4]
2. ![]() Б [1;4]
Б [1;4]
3. ![]() В [–0,25;0,5]
В [–0,25;0,5]
4. ![]() Г [2;5]
Г [2;5]
Д [–1;3]
Частина третя
3.1. Розв’язати рівняння ![]() .
.
3.2. Розв’язати нерівність ![]() .
.
Варіант 3
Частина перша
1.1. Розв’язати рівняння х12=1.
А)![]() ; Б) 1; В) 1;1; Г) хбудь-яке число.
; Б) 1; В) 1;1; Г) хбудь-яке число.
1.2. Розв’язати рівняння lg(x+5)=2.
А) 95; Б) 3; В) 105; Г) 5.
1.3. Розв’язати нерівність log0,4 x < log0,4 8.
А) (∞;8) ; Б) (0;8); В) (0,4;8) ; Г) (8;∞).
1.4. Розв’язати нерівність 0,5х < 0,25.
А) (2;∞) ; Б) (–∞;2) ; В) (–2;∞) ; Г) (–∞;–2).
1.5. Розв’язати рівняння log2 log2 log3 x = 0.
А) 9; Б) 8; В) 4; Г) 3.
Частина друга
2.1. Установити відповідність між нерівностями (1–4) і множинами їх розв’язків (А–Д):
1. ![]() А (–2;0)
А (–2;0)
2. ![]() Б (–∞;2)
Б (–∞;2)
3. ![]() В (3;+∞)
В (3;+∞)
4. ![]() Г (–4;–2)
Г (–4;–2)
Д (0;3)
Частина третя
3.1. Розв’язати рівняння ![]() .
.
3.2. Розв’язати нерівність 4х ∙ 2![]() >16.
>16.
Варіант 4
Частина перша
1.1. Розв’язати рівняння ![]() .
.
А) 0; Б) 2;0; В) 0;2; Г) коренів немає.
1.2. Розв’язати рівняння log6 x = 2.
А) 12; Б) 36; В) ![]() ; Г)
; Г) ![]() .
.
1.3. Розв’язати нерівність ![]() .
.
А) (5; ∞); Б) (∞;5); В) (0;5); Г) (0;5)U(5;∞).
1.4. Розв’язати нерівність 0,2 х–2 0,008.
А) [5;∞); Б) (–∞;5]; В) (–∞;4]; Г) [4;∞).
1.5. Яка нерівність не має розв’язків?
А) lg x > 0; Б) lg (x) >0; В) lg x lg (x); Г) lg x2 < 0.
Частина друга
2.1. Установити відповідність між рівняннями (1–4) та їх розв’язками(А–Д):
1. ![]() А Ø
А Ø
2. ![]() Б –1
Б –1
3. 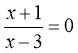 В 3
В 3
4. ![]() Г 8
Г 8
Д 21
Частина третя
3.1. Розв’язати рівняння ![]()
3.2. Розв’язати нерівність 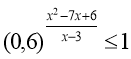 .
.

про публікацію авторської розробки
Додати розробку
